第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
1. 如果+50 m表示向右走50 m,那么向左走50 m记作(
A.-50 m
B.+50 m
C.-100 m
D.+100 m
A
).A.-50 m
B.+50 m
C.-100 m
D.+100 m
答案:
解:根据题意,向右走记为“+”,则向左走记为“-”,所以向左走50 m记作-50 m。
答案:A
答案:A
2. 下列不是具有相反意义的量的是(
A.前进6 m和后退8 m
B.收入20元和支出10元
C.向东走4 m和向北走9 m
D.超过5 g和不足3 g
C
).A.前进6 m和后退8 m
B.收入20元和支出10元
C.向东走4 m和向北走9 m
D.超过5 g和不足3 g
答案:
解:具有相反意义的量需满足两个条件:①意义相反;②都具有数量。
A. 前进与后退意义相反,且都有数量,是相反意义的量;
B. 收入与支出意义相反,且都有数量,是相反意义的量;
C. 向东与向北方向不相反,不是相反意义的量;
D. 超过与不足意义相反,且都有数量,是相反意义的量。
答案:C
A. 前进与后退意义相反,且都有数量,是相反意义的量;
B. 收入与支出意义相反,且都有数量,是相反意义的量;
C. 向东与向北方向不相反,不是相反意义的量;
D. 超过与不足意义相反,且都有数量,是相反意义的量。
答案:C
3. 有一种记分方法:以60分为标准,68分记作+8分.某同学得54分,则应记作
-6
分.
答案:
【解析】:
题目考查了正数和负数在实际问题中的应用,特别是如何用正负数来表示与标准值的偏差。
首先,确定标准分值为60分。
然后,根据题目,68分与标准分值60分的偏差是+8分,这是通过$68 - 60 = 8$计算得出的。
同样地,某同学得54分,需要计算54分与标准分值60分的偏差。
这个偏差是$54 - 60 = -6$分。
因此,54分应记作-6分。
【答案】:
-6分。
题目考查了正数和负数在实际问题中的应用,特别是如何用正负数来表示与标准值的偏差。
首先,确定标准分值为60分。
然后,根据题目,68分与标准分值60分的偏差是+8分,这是通过$68 - 60 = 8$计算得出的。
同样地,某同学得54分,需要计算54分与标准分值60分的偏差。
这个偏差是$54 - 60 = -6$分。
因此,54分应记作-6分。
【答案】:
-6分。
4. 已知下列各数:$-2\frac{3}{4},$+3,0,-2024,36,$\frac{1}{2},$其中正数有
$+3$,$36$,$\frac{1}{2}$
;负数有$-2\frac{3}{4}$,$-2024$
;既不是正数,也不是负数的是$0$
.
答案:
【解析】:
题目要求识别给定数列中的正数、负数和既不是正数也不是负数的数。
首先,需要明确什么是正数、负数和零。
正数是大于零的数,负数是小于零的数,零既不是正数也不是负数。
接下来,逐一判断每个数的属性:
$-2\frac{3}{4}$ 是一个负数,因为它小于零。
$+3$ 是一个正数,因为它大于零。
$0$ 既不是正数也不是负数。
$-2024$ 是一个负数,因为它小于零。
$36$ 是一个正数,因为它大于零。
$\frac{1}{2}$ 是一个正数,因为它大于零。
根据以上分析,可以将这些数分类为正数、负数和零。
【答案】:
正数有 $+3$,$36$,$\frac{1}{2}$;
负数有 $-2\frac{3}{4}$,$-2024$;
既不是正数也不是负数的是 $0$。
题目要求识别给定数列中的正数、负数和既不是正数也不是负数的数。
首先,需要明确什么是正数、负数和零。
正数是大于零的数,负数是小于零的数,零既不是正数也不是负数。
接下来,逐一判断每个数的属性:
$-2\frac{3}{4}$ 是一个负数,因为它小于零。
$+3$ 是一个正数,因为它大于零。
$0$ 既不是正数也不是负数。
$-2024$ 是一个负数,因为它小于零。
$36$ 是一个正数,因为它大于零。
$\frac{1}{2}$ 是一个正数,因为它大于零。
根据以上分析,可以将这些数分类为正数、负数和零。
【答案】:
正数有 $+3$,$36$,$\frac{1}{2}$;
负数有 $-2\frac{3}{4}$,$-2024$;
既不是正数也不是负数的是 $0$。
5. 在产品质量检测中,从标准质量为每盒125 g的酸奶中抽取6盒,结果如下:
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 质量/g | 126 | 127 | 124 | 126 | 123 | 125 |
| 差值/g | +1 |
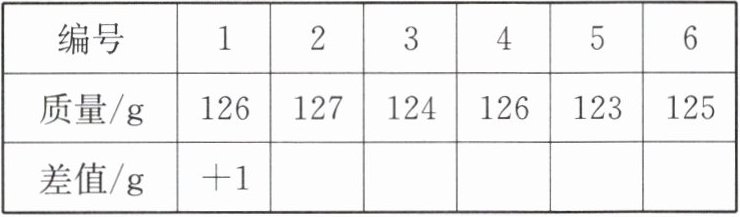
(1)请补全表格中相关数据.
(2)请列式计算这6盒酸奶的总质量.
(1)表格中相关数据从上到下依次为:+2;-1;+1;-2;0。
(2)这6盒酸奶的总质量为751g。
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 质量/g | 126 | 127 | 124 | 126 | 123 | 125 |
| 差值/g | +1 |
+2
| -1
| +1
| -2
| 0
|
(1)请补全表格中相关数据.
(2)请列式计算这6盒酸奶的总质量.
(1)表格中相关数据从上到下依次为:+2;-1;+1;-2;0。
(2)这6盒酸奶的总质量为751g。
答案:
【解析】:
本题主要考查正负数的实际应用和有理数的加法运算。
(1)首先,需要补全表格中的差值数据。
根据题目,标准质量为每盒$125g$,可以通过计算每盒酸奶的质量与标准质量的差值来得到差值数据。
对于编号2:$127 - 125 = +2$,
对于编号3:$124 - 125 = -1$,
对于编号4:$126 - 125 = +1$,
对于编号5:$123 - 125 = -2$,
对于编号6:$125 - 125 = 0$。
(2)接下来,计算这6盒酸奶的总质量。
可以通过将每盒酸奶的质量相加来得到总质量,
即:$126 + 127 + 124 + 126 + 123 + 125 = 751(g)$。
另一种方法是通过计算差值来得到总质量。
首先,计算所有差值的和:$1 + 2 - 1 + 1 - 2 + 0 = 1(g)$。
然后,将这个和加到6盒酸奶的标准总质量上,
即:$6 × 125 + 1 = 750 + 1 = 751(g)$。
【答案】:
(1)表格中相关数据从上到下依次为:+2;-1;+1;-2;0。
(2)这6盒酸奶的总质量为$751g$。
本题主要考查正负数的实际应用和有理数的加法运算。
(1)首先,需要补全表格中的差值数据。
根据题目,标准质量为每盒$125g$,可以通过计算每盒酸奶的质量与标准质量的差值来得到差值数据。
对于编号2:$127 - 125 = +2$,
对于编号3:$124 - 125 = -1$,
对于编号4:$126 - 125 = +1$,
对于编号5:$123 - 125 = -2$,
对于编号6:$125 - 125 = 0$。
(2)接下来,计算这6盒酸奶的总质量。
可以通过将每盒酸奶的质量相加来得到总质量,
即:$126 + 127 + 124 + 126 + 123 + 125 = 751(g)$。
另一种方法是通过计算差值来得到总质量。
首先,计算所有差值的和:$1 + 2 - 1 + 1 - 2 + 0 = 1(g)$。
然后,将这个和加到6盒酸奶的标准总质量上,
即:$6 × 125 + 1 = 750 + 1 = 751(g)$。
【答案】:
(1)表格中相关数据从上到下依次为:+2;-1;+1;-2;0。
(2)这6盒酸奶的总质量为$751g$。
1. 在-1,0,0.2,$\frac{1}{7},$3中,正数的个数为(
A.1
B.2
C.3
D.4
C
).A.1
B.2
C.3
D.4
答案:
【解析】:
题目要求在给定的数中找出正数的个数。正数定义为大于0的数。给定的数有-1,0,0.2,$\frac{1}{7}$,3。
-1不是正数(是负数)
0不是正数
0.2是正数
$\frac{1}{7}$是正数(因为$\frac{1}{7}$大于0)
3是正数
所以,正数有0.2,$\frac{1}{7}$,3,共3个。
【答案】:
C.3
题目要求在给定的数中找出正数的个数。正数定义为大于0的数。给定的数有-1,0,0.2,$\frac{1}{7}$,3。
-1不是正数(是负数)
0不是正数
0.2是正数
$\frac{1}{7}$是正数(因为$\frac{1}{7}$大于0)
3是正数
所以,正数有0.2,$\frac{1}{7}$,3,共3个。
【答案】:
C.3
2. 在-8,+4.3,0,$-\frac{1}{2},$3中,正数有
+4.3, 3
;负数有$-8, -\frac{1}{2}$
;既不是正数,也不是负数的是0
.
答案:
【解析】:
题目考查正数、负数和0的定义。正数是大于0的数,负数是小于0的数,0既不是正数也不是负数。根据这些定义,我们需要在给定的数中筛选出正数、负数和0。
【答案】:
正数有 $+4.3, 3$;
负数有 $-8, -\frac{1}{2}$;
既不是正数,也不是负数的是 $0$。
题目考查正数、负数和0的定义。正数是大于0的数,负数是小于0的数,0既不是正数也不是负数。根据这些定义,我们需要在给定的数中筛选出正数、负数和0。
【答案】:
正数有 $+4.3, 3$;
负数有 $-8, -\frac{1}{2}$;
既不是正数,也不是负数的是 $0$。
3.(2024云南)中国是最早使用正负数表示具有相反意义的量的国家.若向北运动100 m记作+100 m,则向南运动100 m可记作(
A.100 m
B.-100 m
C.200 m
D.-200 m
B
).A.100 m
B.-100 m
C.200 m
D.-200 m
答案:
解:向北运动100m记作+100m,向南与向北是相反意义的量,所以向南运动100m可记作-100m。
答案:B
答案:B
4.(教材练习变式)中国古代著作《九章算术》在世界数学史上首次正式引入负数.如果将气温4℃记作+4℃,那么气温零下5℃可记作
-5℃
.
答案:
【解析】:本题考查正数和负数的概念。在数学中,正数和负数用来表示相反意义的量。
题目中已给出气温$4℃$记作$+4℃$,表示零上的气温用正数表示。
由此推断,零下的气温应用负数表示。因此,气温零下$5℃$应记作带有负号的数值,即$-5℃$。
【答案】:$- 5℃$
题目中已给出气温$4℃$记作$+4℃$,表示零上的气温用正数表示。
由此推断,零下的气温应用负数表示。因此,气温零下$5℃$应记作带有负号的数值,即$-5℃$。
【答案】:$- 5℃$
5. 小明练习跳绳,以1分钟跳165次为标准,并把5组1分钟跳绳的次数记录如下(用正数表示超过标准的次数,用负数表示少于标准的次数):-11,-6,-2,+4,+10.
(1)小明在这5组跳绳练习中,1分钟最多跳多少次?
(2)小明在这5组跳绳练习中,1分钟跳绳次数最多的一组比最少的一组多几次?
(3)小明在这5组跳绳练习中,累计跳绳多少次?
(1)小明在这5组跳绳练习中,1分钟最多跳多少次?
(2)小明在这5组跳绳练习中,1分钟跳绳次数最多的一组比最少的一组多几次?
(3)小明在这5组跳绳练习中,累计跳绳多少次?
答案:
(1)解:165 + 10 = 175(次)
答:1分钟最多跳175次。
(2)解:最多的次数为175次,最少的次数为165 + (-11) = 154(次)
175 - 154 = 21(次)
答:最多的一组比最少的一组多21次。
(3)解:165×5 + (-11) + (-6) + (-2) + 4 + 10 = 825 - 11 - 6 - 2 + 4 + 10 = 820(次)
答:累计跳绳820次。
(1)解:165 + 10 = 175(次)
答:1分钟最多跳175次。
(2)解:最多的次数为175次,最少的次数为165 + (-11) = 154(次)
175 - 154 = 21(次)
答:最多的一组比最少的一组多21次。
(3)解:165×5 + (-11) + (-6) + (-2) + 4 + 10 = 825 - 11 - 6 - 2 + 4 + 10 = 820(次)
答:累计跳绳820次。
查看更多完整答案,请扫码查看


