第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
1. (综合与实践)(人教教材 P86“探究与发现”改编)探索三角形边与角之间的不等关系. 我们知道,在一个三角形中,相等的边所对的角相等,那么不相等的边所对的角之间的大小关系是怎样的呢?
【观察猜想】(1)在$\triangle ABC$中,$AB>AC$,猜想$∠C$与$∠B$之间的大小关系;
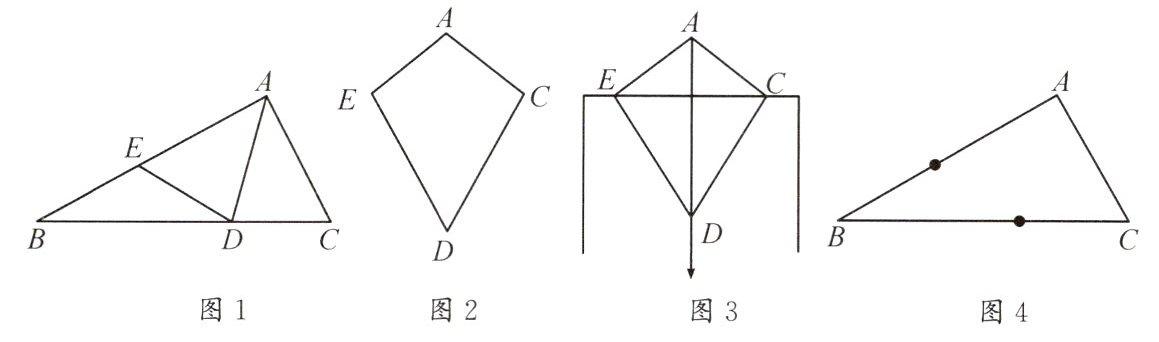
【操作证明】(2)如图 1,某同学发现在$\triangle ABC$中,若$AB>AC$,可将$\triangle ABC$折叠,使边$AC$落在$AB$上,点$C$落在边$AB$上的点$E$,折线交$BC$于点$D$,连接$ED$,发现$∠AED=∠B+∠EDB,\cdot \cdot \cdot$,请用上述思路证明(1)中猜想的结论;
【操作发现】同学们用类似操作继续折纸探究“大边对大角,大角对大边”,发现图 1 中的四边形$AEDC$,满足$AE=AC,DE=DC$,查阅资料,如图 2,有两组邻边分别相等的四边形叫作“筝形”.
【拓展应用】(3)资料显示,“筝形”仪器可用于检测门框是否水平. 如图 3,“筝形”仪器$AEDC$上的点$A$处绑一条线绳,线绳另一端挂一个铅锤. 某同学将仪器上的点$E,C$紧贴门框上方,观察若线绳恰好经过点$D$,则可判断门框是水平的. 请说明此同学做法的理由;
(4)如图 4,在$\triangle ABC$中,$∠A=90^{\circ },∠B=30^{\circ }$,点$E,F$分别是边$AB,BC$上的动点. 当四边形$AEFC$为“筝形”时,请直接写出$∠BFE$的度数.
【观察猜想】(1)在$\triangle ABC$中,$AB>AC$,猜想$∠C$与$∠B$之间的大小关系;
【操作证明】(2)如图 1,某同学发现在$\triangle ABC$中,若$AB>AC$,可将$\triangle ABC$折叠,使边$AC$落在$AB$上,点$C$落在边$AB$上的点$E$,折线交$BC$于点$D$,连接$ED$,发现$∠AED=∠B+∠EDB,\cdot \cdot \cdot$,请用上述思路证明(1)中猜想的结论;
【操作发现】同学们用类似操作继续折纸探究“大边对大角,大角对大边”,发现图 1 中的四边形$AEDC$,满足$AE=AC,DE=DC$,查阅资料,如图 2,有两组邻边分别相等的四边形叫作“筝形”.
【拓展应用】(3)资料显示,“筝形”仪器可用于检测门框是否水平. 如图 3,“筝形”仪器$AEDC$上的点$A$处绑一条线绳,线绳另一端挂一个铅锤. 某同学将仪器上的点$E,C$紧贴门框上方,观察若线绳恰好经过点$D$,则可判断门框是水平的. 请说明此同学做法的理由;
(4)如图 4,在$\triangle ABC$中,$∠A=90^{\circ },∠B=30^{\circ }$,点$E,F$分别是边$AB,BC$上的动点. 当四边形$AEFC$为“筝形”时,请直接写出$∠BFE$的度数.

答案:
解:
(1)猜想:$∠C>∠B$.
(2)证明:由折叠,可得$AC=AE$,$∠C=∠AED$.
$\because ∠AED=∠B+∠EDB$,
$\therefore ∠C=∠B+∠EDB$.
$\therefore ∠C>∠B$.
(3)理由如下:$\because AE=AC$,$DE=DC$,
$\therefore AD$垂直平分$EC$.
$\therefore AD⊥EC$.
$\because AD$是铅锤线,
$\therefore EC$是水平的,即门框是水平的.
(4)$∠BFE$的度数为$30^{\circ}$或$90^{\circ}$.
(1)猜想:$∠C>∠B$.
(2)证明:由折叠,可得$AC=AE$,$∠C=∠AED$.
$\because ∠AED=∠B+∠EDB$,
$\therefore ∠C=∠B+∠EDB$.
$\therefore ∠C>∠B$.
(3)理由如下:$\because AE=AC$,$DE=DC$,
$\therefore AD$垂直平分$EC$.
$\therefore AD⊥EC$.
$\because AD$是铅锤线,
$\therefore EC$是水平的,即门框是水平的.
(4)$∠BFE$的度数为$30^{\circ}$或$90^{\circ}$.
查看更多完整答案,请扫码查看


