第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
3. 1751年,瑞士数学家欧拉(Euler,1707-1783)向德国-俄国数学家哥德巴赫(Goldbach,1690-1764)提出了一个n边形的三角剖分有多少种不同方法的问题,并归纳得出了n边形的不同三角剖分方法数$(D_{n})$的公式。后来数学家发现并证明:当$n≥3$时,$\frac {D_{n+1}}{D_{n}}=\frac {4n-6}{n}(D_{3}=1)$。请你利用此公式,计算$D_{6}$的值为______
14
。
答案:
14
4. 数学史上著名的“哥尼斯堡七桥问题(图1)”的解决开创了数学的一个新分支:图论。图论是一门研究点、线、面(面是由线所围成的区域,区域之间不重合)这三个构成所有几何图形的基本要素的学科。在十八世纪初,瑞士数学家欧拉通过把图1转化为图2,找出了几何图形中点、线、面之间的数量关系,人称欧拉公式,该公式深刻揭示了几何图形的本质属性。
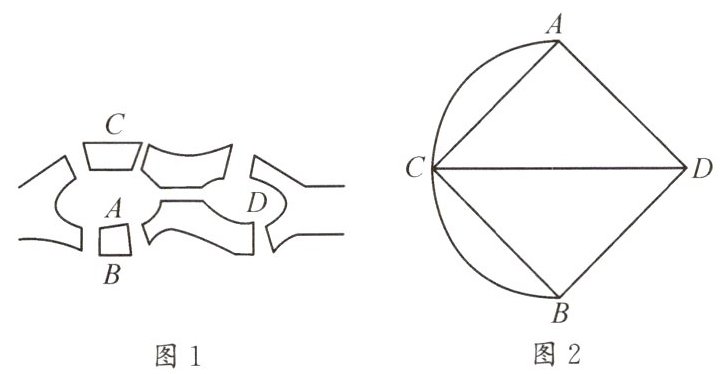
(1)设四边形的顶点数为V,边数为E,区域数为F,则V=
(2)将五边形用同一点引出的对角线分割成若干个三角形(如图3),设这种分割中图案的顶点数为V,边数为E,区域数为F(区域之间不重合),则V,E,F之间的数量关系为
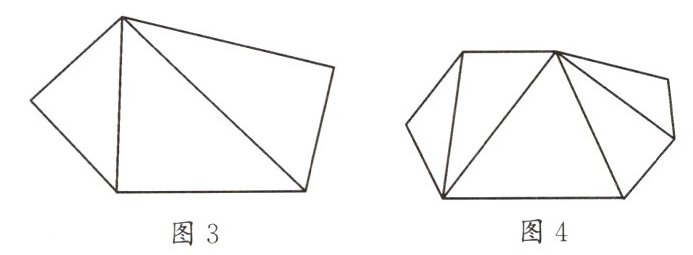
(3)将n边形$(n≥3)$用互不相交的对角线分割成若干个三角形,构成类似图4的图案,设这种分割中图案的顶点数为V,边数为E,区域数为F(区域之间不重合),则V,E,F的数量关系为

(1)设四边形的顶点数为V,边数为E,区域数为F,则V=
4
,E=4
,F=1;(2)将五边形用同一点引出的对角线分割成若干个三角形(如图3),设这种分割中图案的顶点数为V,边数为E,区域数为F(区域之间不重合),则V,E,F之间的数量关系为
$ V - E + F = 1 $
;(用V,E,F表示)
(3)将n边形$(n≥3)$用互不相交的对角线分割成若干个三角形,构成类似图4的图案,设这种分割中图案的顶点数为V,边数为E,区域数为F(区域之间不重合),则V,E,F的数量关系为
$ V - E + F = 1 $
。
答案:
(1) 4 4
(2) $ V - E + F = 1 $
(3) $ V - E + F = 1 $
(1) 4 4
(2) $ V - E + F = 1 $
(3) $ V - E + F = 1 $
查看更多完整答案,请扫码查看


