第132页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
$x^{2}+(p+q)x+pq$型式子是数学学习中常见的一类多项式,如何将这种类型的式子进行因式分解呢?我们发现,$(x+p)(x+q)=x^{2}+(p+q)x+pq$。这个规律可以利用多项式的乘法法则推导得出:$(x+p)(x+q)=x^{2}+px+qx+pq=x^{2}+(p+q)x+pq$。
因式分解是与整式乘法方向相反的变形,利用这种关系可得
$x^{2}+(p+q)x+pq=(x+p)(x+q)$。(*)
利用(*)式可以将某些二次项系数是1的二次三项式分解因式。例如,将式子$x^{2}+3x+2$分解因式。这个式子的二次项系数是1,常数项$2=1×2$,一次项系数$3=1+2$,因此这是一个$x^{2}+(p+q)x+pq$型的式子。利用(*)式可得$x^{2}+3x+2=(x+1)(x+2)$。
上述分解因式$x^{2}+3x+2$的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图)。
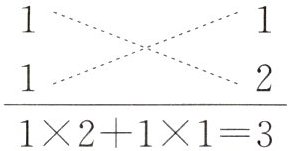
这样,我们也可以得到$x^{2}+3x+2=(x+1)(x+2)$。
【尝试】利用这种方法,你能把下列多项式分解因式吗?
(1)$x^{2}+7x+10$;(2)$x^{2}-2x-8$;
(3)$y^{2}-7y+12$;(4)$x^{2}+7x-18$。
【拓展】类似这种方法,请对下列二次项系数不为1的多项式分解因式。
(5)$2x^{2}+9x+7$;(6)$3x^{2}-8x+4$。
因式分解是与整式乘法方向相反的变形,利用这种关系可得
$x^{2}+(p+q)x+pq=(x+p)(x+q)$。(*)
利用(*)式可以将某些二次项系数是1的二次三项式分解因式。例如,将式子$x^{2}+3x+2$分解因式。这个式子的二次项系数是1,常数项$2=1×2$,一次项系数$3=1+2$,因此这是一个$x^{2}+(p+q)x+pq$型的式子。利用(*)式可得$x^{2}+3x+2=(x+1)(x+2)$。
上述分解因式$x^{2}+3x+2$的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图)。
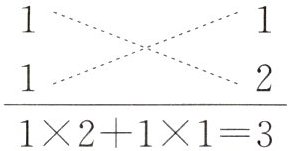
这样,我们也可以得到$x^{2}+3x+2=(x+1)(x+2)$。
【尝试】利用这种方法,你能把下列多项式分解因式吗?
(1)$x^{2}+7x+10$;(2)$x^{2}-2x-8$;
(3)$y^{2}-7y+12$;(4)$x^{2}+7x-18$。
【拓展】类似这种方法,请对下列二次项系数不为1的多项式分解因式。
(5)$2x^{2}+9x+7$;(6)$3x^{2}-8x+4$。
答案:
(1)原式$=(x+5)(x+2)$.
(2)原式$=(x-4)(x+2)$.
(3)原式$=(y-3)(y-4)$.
(4)原式$=(x-2)(x+9)$.
(5)原式$=(2x+7)(x+1)$.
(6)原式$=(3x-2)(x-2)$.
(1)原式$=(x+5)(x+2)$.
(2)原式$=(x-4)(x+2)$.
(3)原式$=(y-3)(y-4)$.
(4)原式$=(x-2)(x+9)$.
(5)原式$=(2x+7)(x+1)$.
(6)原式$=(3x-2)(x-2)$.
查看更多完整答案,请扫码查看


