《2025年多维导学案八年级数学上册人教版》

活动1 月历中的奥秘
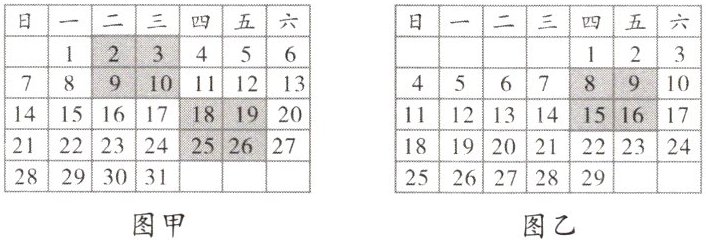
在日历上，我们会发现其中某些数满足的一些规律，如图甲是2024年元月份的日历.我们任意选择其中所示的方框部分，将每个方框部分中4个位置上的数交叉相乘，再相减，例如：
3×9−2×10=27−20=7，
19×25−18×26=475−468=7，
不难发现结果都是7.
(1)如图乙是2024年2月份的日历，在图乙中类似的部分试一试，看看是否存在同样的规律；
(2)设某一类似部分最左上角的数字为x，请你利用整式的运算对以上的规律加以证明.

答案： 解：
(1)$9×15 - 8×16 = 135 - 128 = 7$。在图乙中也存在同样的规律。
(2)证明：某一类似部分最左上角的数字为$x$，则左下角的数字为$x + 7$，右上角的数字为$x + 1$，右下角的数字是$x + 8$。根据题意，得$(x + 1)(x + 7) - x(x + 8) = x^{2} + 8x + 7 - x^{2} - 8x = 7$。

活动2 和为定值的两数积的规律
(1)计算下列两个数的和(每组中两个数的和为定值)，你能发现结果有什么规律吗?
①30×30，35×25，43×17，52×8；
②50×50，53×47，74×26，91×9.
(2)你能用本章所学知识解释你发现的规律吗?
(3)利用你发现的规律解决下面问题：用10m长的绳子围成一个长方形，长方形的最大面积是多少?此时长方形的两条邻边长有什么关系?你能得出更一般的结论吗?

答案： 解：
(1)①$30×30 = 900$，$35×25 = 875$，$43×17 = 731$，$52×8 = 416$；②$50×50 = 2500$，$53×47 = 2491$，$74×26 = 1924$，$91×9 = 819$。规律：两个正数的和为定值，当两数相等时，它们的乘积最大。
(2)证明：设两个正数分别为$a$，$b$，它们的和为$2n$。设$a = n + m$，$b = n - m$，则$ab = (n + m)(n - m) = n^{2} - m^{2}$。当两数相等时，$m = 0$。此时$ab = n^{2} - m^{2}$取得最大值。$\therefore$两个正数的和为定值时，当两数相等时，它们的乘积最大。
(3)设长方形的长和宽分别为$x$，$y$，面积为$S$，由题意，得$S = xy$，$2(x + y) = 10$，$\therefore x + y = 5$是一个定值。由
(2)知，当$x = y = 2.5$时，$S$取得最大值，最大值$S = 2.5×2.5 = 6.25$。$\therefore$长方形的最大面积是$6.25m^{2}$，此时长方形的两条邻边长相等，即所围成的图形是正方形。结论：长方形的周长为定值时，当长方形是正方形时，面积最大。