第200页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
跟踪训练2 已知直线$l:y = kx$与椭圆$E:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$($a>b>0$)交于$A$,$B$两点,$M$是椭圆上异于$A$,$B$的一点. 若椭圆$E$的离心率的取值范围是$(\frac{\sqrt{3}}{3},\frac{\sqrt{2}}{2})$,则直线$MA$,$MB$斜率之积的取值范围是( )
A. $(-\frac{\sqrt{2}}{2},-\frac{1}{2})$
B. $(-\frac{1}{2},-\frac{1}{4})$
C. $(-\frac{\sqrt{3}}{2},-\frac{\sqrt{2}}{2})$
D. $(-\frac{2}{3},-\frac{1}{2})$
A. $(-\frac{\sqrt{2}}{2},-\frac{1}{2})$
B. $(-\frac{1}{2},-\frac{1}{4})$
C. $(-\frac{\sqrt{3}}{2},-\frac{\sqrt{2}}{2})$
D. $(-\frac{2}{3},-\frac{1}{2})$
答案:
跟踪训练2D [由椭圆中的结论,可得kMA.kMβ=-$\frac{b²}{a²}$,
由椭圆的离心率的取值范围是($\frac{\sqrt{3}}{3}$,$\frac{\sqrt{2}}{2}$),
即$\frac{\sqrt{3}}{3}$<e<$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{3}$<$\frac{C}{a}$<$\frac{√2}{2}$-$\frac{1}{3}$<($\frac{C}{a}$)²<$\frac{1}{2}$,
所以$\frac{1}{3}$<$\frac{a²-b²}{a²}$<$\frac{1}{2}$→一$\frac{2}{3}$<一$\frac{b}{a²}$
<一$\frac{1}{2}$,
即一$\frac{2}{3}$<KMA.kMB<一$\frac{1}{2}$.]
命题点3 切线、切点弦方程
例3 椭圆$C_1:\frac{x^{2}}{2}+y^{2}=1$,$O$为坐标原点,点$B$为$C_1$在第一象限中的任意一点,过$B$作$C_1$的切线$l$,$l$分别与$x$轴和$y$轴的正半轴交于$C$,$D$两点,则$\triangle OCD$面积的最小值为( )
A. 1
B. $\sqrt{3}$
C. $\sqrt{2}$
D. 2
例3 椭圆$C_1:\frac{x^{2}}{2}+y^{2}=1$,$O$为坐标原点,点$B$为$C_1$在第一象限中的任意一点,过$B$作$C_1$的切线$l$,$l$分别与$x$轴和$y$轴的正半轴交于$C$,$D$两点,则$\triangle OCD$面积的最小值为( )
A. 1
B. $\sqrt{3}$
C. $\sqrt{2}$
D. 2
答案:
例3C [设B(x,y1)(x²>0,y1>0),由题意得,过点B的切线!的方程为$\frac{x.}{2}$+yy=1.
令y=0,可得c{$\frac{2}{x}$,0),
令x=0,可得D(0,$\frac{1}{y}$),
所以△OCD的面积
S=$\frac{1}{2}$.$\frac{2}{Xi}$.$\frac{1}{y}$=$\frac{1}{y}$,
又点B在椭圆上,所以$\frac{xi}{2}$+y=1,所以S=$\frac{1}{xy}$=$\frac{2+yi}{xy}$$\frac{xi}{2}$ =2x元:+$\frac{}{i}$
≥2 $\sqrt{\frac{}{X}}$=√2,
当且仅当2xy¹=$\frac{1}{I1}$,即x1=1,y!=$\frac{2}{2}$
时等号成立,
所以△OCD面积的最小值为√2.]
跟踪训练3 点$P$为直线$l:y=\frac{1}{4}x + 1$上一动点,过$P$作双曲线$\frac{x^{2}}{4}-y^{2}=1$的切线$PA$,$PB$,切点分别为$A$,$B$,则直线$AB$过定点______.
答案:
跟踪训练3(-1,-1)
解析 设P(x。,y。),A(x..y;),
B(x2,y2),
则PA,PB的方程分别为
$\frac{xx}{4}$-yy=1,x42x-y2y=1,
因为点P在两条直线上
所以$\frac{x、x。}{4}$-y1口=1,x²x|-y2y。=1.
-y。y 这表明,。点A,B都在{线$\frac{xox}{4}$
=1上,
即直线AB的方程为$\frac{ox}{4}$-y。y=1.又y。=+1,
代入整理得4(x-y)-(y+1)=0,令{0+10),=o解得(二二111..
即直线AB过定点(-1,-1).
例4 (1)已知$A$,$B$是过抛物线$y^{2}=2px$($p>0$)焦点$F$的直线与抛物线的交点,$O$是坐标原点,且满足$\overrightarrow{AB}=3\overrightarrow{FB}$,$S_{\triangle OAB}=\frac{\sqrt{2}}{3}|AB|$,则$|AB|$的值为( )
A. $\frac{9}{2}$ B. $\frac{2}{9}$ C. 4 D. 2
(2)已知抛物线方程为$y^{2}=2px$($p>0$),$O$为坐标原点,过抛物线焦点$F$的直线交抛物线于$A$,$B$两点,$A$,$B$的纵坐标之积为$-8$,且$|AF| = 3|BF|$,则$\triangle OAB$的面积是( )
A. $4\sqrt{2}$ B. $\frac{1}{4}$ C. $\frac{4\sqrt{3}}{3}$ D. $\frac{8\sqrt{3}}{3}$
A. $\frac{9}{2}$ B. $\frac{2}{9}$ C. 4 D. 2
(2)已知抛物线方程为$y^{2}=2px$($p>0$),$O$为坐标原点,过抛物线焦点$F$的直线交抛物线于$A$,$B$两点,$A$,$B$的纵坐标之积为$-8$,且$|AF| = 3|BF|$,则$\triangle OAB$的面积是( )
A. $4\sqrt{2}$ B. $\frac{1}{4}$ C. $\frac{4\sqrt{3}}{3}$ D. $\frac{8\sqrt{3}}{3}$
答案:
例4
(1)A [如图,不 妨令直线AB的倾斜 角为α,α∈(0,/|),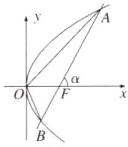
∵AB=3FB.
∴F为 AB的三等分点, 令|BF|=t, 则|AF1=2t, 由$\frac{1}{IBFI}$+$\frac{1}{IAFI}$=$\frac{2}{p}$, 得$\frac{1}{t}$+$\frac{1}{2}$=$\frac{2}{p}$→t=$\frac{3}{4}$ρ,
∴|AB|=3t=$\frac{9}{4}$p, 又|AB|=$\frac{2p}{sin²a}$,
∴$\frac{2p}{sin²a}$=$\frac{9}{4}$p→sinα=$\frac{2√2}{3}$, 又S△OAB=$\frac{2}{3}$|AB1,
∴$\frac{1}{2sina}$=$\frac{2}{3}$|AB1, 即4$\sqrt{2}$=$\frac{√2}{3}$.$\frac{9}{4}$P→p=2, 3
∴|AB|=$\frac{9}{2}$.]
(2)D [不妨令A(xA.yA)在第一象限,B(xβ.yB)在第四象限, 则yAyβ=-p²=-8,所以p=2$\sqrt{2}$ 又即因|y为A||A=F3||=yβ31|B,代F|入,所y以Ay|Hy一y=AB-|=83,,可得3y=8,由于B在第四象限,则yβ=一$\frac{2\sqrt{6}}{3}$,所以yA=2$\sqrt{6}$ 所以S(Aβ=$\frac{1}{2}$OF1,|yA-yβ|=$\frac{8/3}{3}$.]
例4
(1)A [如图,不 妨令直线AB的倾斜 角为α,α∈(0,/|),

∵AB=3FB.
∴F为 AB的三等分点, 令|BF|=t, 则|AF1=2t, 由$\frac{1}{IBFI}$+$\frac{1}{IAFI}$=$\frac{2}{p}$, 得$\frac{1}{t}$+$\frac{1}{2}$=$\frac{2}{p}$→t=$\frac{3}{4}$ρ,
∴|AB|=3t=$\frac{9}{4}$p, 又|AB|=$\frac{2p}{sin²a}$,
∴$\frac{2p}{sin²a}$=$\frac{9}{4}$p→sinα=$\frac{2√2}{3}$, 又S△OAB=$\frac{2}{3}$|AB1,
∴$\frac{1}{2sina}$=$\frac{2}{3}$|AB1, 即4$\sqrt{2}$=$\frac{√2}{3}$.$\frac{9}{4}$P→p=2, 3
∴|AB|=$\frac{9}{2}$.]
(2)D [不妨令A(xA.yA)在第一象限,B(xβ.yB)在第四象限, 则yAyβ=-p²=-8,所以p=2$\sqrt{2}$ 又即因|y为A||A=F3||=yβ31|B,代F|入,所y以Ay|Hy一y=AB-|=83,,可得3y=8,由于B在第四象限,则yβ=一$\frac{2\sqrt{6}}{3}$,所以yA=2$\sqrt{6}$ 所以S(Aβ=$\frac{1}{2}$OF1,|yA-yβ|=$\frac{8/3}{3}$.]
跟踪训练4 (1)斜率为$\sqrt{3}$的直线经过抛物线$y^{2}=2px$($p>0$)的焦点$F$且与抛物线交于$A$,$B$两点,$A$在第一象限且$|AF| = 4$,则$|AB|=$______.
(2)(2023·长沙模拟)已知抛物线$C:y^{2}=16x$,倾斜角为$\frac{\pi}{6}$的直线$l$过焦点$F$交抛物线于$A$,$B$两点,$O$为坐标原点,则$\triangle ABO$的面积为______.
(3)(2023·“四省八校”联考)已知抛物线$y^{2}=4x$,过焦点$F$的直线与抛物线交于$A$,$B$两点,则$2|AF|+|BF|$的最小值为______.
(2)(2023·长沙模拟)已知抛物线$C:y^{2}=16x$,倾斜角为$\frac{\pi}{6}$的直线$l$过焦点$F$交抛物线于$A$,$B$两点,$O$为坐标原点,则$\triangle ABO$的面积为______.
(3)(2023·“四省八校”联考)已知抛物线$y^{2}=4x$,过焦点$F$的直线与抛物线交于$A$,$B$两点,则$2|AF|+|BF|$的最小值为______.
答案:
跟踪训练4
(1)$\frac{16}{3}$ 解析 直线1的倾斜 角α=60°, 由|AF|=$\frac{p}{1-cOSa}$ =4,得
p=4(1-cosa)=2,
=4,得
p=4(1-cosa)=2,
∴|AB|=$\frac{2p}{sina}$ =$\frac{4}{3}$=$\frac{16}{3}$ 4
(2)64 解析 依题意,抛物线y²=16x,p=8.又!的倾斜角α=$\frac{π}{6}$: 所以S△OAB=$\frac{p}{2sina}$= 8² =64. 2sin$\frac{π}{6}$
(3)3+2$\sqrt{2}$ 解析 因为p=2, 所以$\frac{1}{AF1}$+$\frac{1}{|BFI}$=$\frac{2}{p}$=1, 所以21AF|+IBFI =(2|AF|+|BF|).($\frac{1}{AF}$+$\frac{1}{BF}$) =3+$\frac{21AF}{IBFI}$+$\frac{IBF}{IAF1}$ ≥3+2 $\frac{2A}{IBF}$$\sqrt{.\frac{BF}{IAFI}}$=3+2$\sqrt{2}$ 当且仅当|BF|=$\sqrt{2}$IAF1,即IAF|= $\frac{2}{2}$+1,|BF|=√2+1时,等号成立,因此,2{AF|+|BF|的最小值为3+2√2.
跟踪训练4
(1)$\frac{16}{3}$ 解析 直线1的倾斜 角α=60°, 由|AF|=$\frac{p}{1-cOSa}$
 =4,得
p=4(1-cosa)=2,
=4,得
p=4(1-cosa)=2,∴|AB|=$\frac{2p}{sina}$ =$\frac{4}{3}$=$\frac{16}{3}$ 4
(2)64 解析 依题意,抛物线y²=16x,p=8.又!的倾斜角α=$\frac{π}{6}$: 所以S△OAB=$\frac{p}{2sina}$= 8² =64. 2sin$\frac{π}{6}$
(3)3+2$\sqrt{2}$ 解析 因为p=2, 所以$\frac{1}{AF1}$+$\frac{1}{|BFI}$=$\frac{2}{p}$=1, 所以21AF|+IBFI =(2|AF|+|BF|).($\frac{1}{AF}$+$\frac{1}{BF}$) =3+$\frac{21AF}{IBFI}$+$\frac{IBF}{IAF1}$ ≥3+2 $\frac{2A}{IBF}$$\sqrt{.\frac{BF}{IAFI}}$=3+2$\sqrt{2}$ 当且仅当|BF|=$\sqrt{2}$IAF1,即IAF|= $\frac{2}{2}$+1,|BF|=√2+1时,等号成立,因此,2{AF|+|BF|的最小值为3+2√2.
查看更多完整答案,请扫码查看


