《2024年步步高大一轮复习讲义高中数学人教A版》

2. (多选)(2023·南宁质检)下列图象中，是函数图象的是 ( )

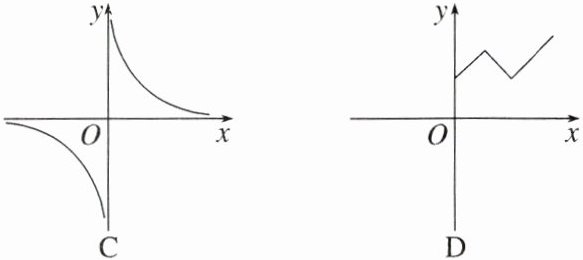
答案： ACD

3. (多选)下列选项中，表示的不是同一个函数的是 ( )
A. $y=\frac{\sqrt{x + 3}}{\sqrt{3 - x}}$与$y=\sqrt{\frac{x + 3}{3 - x}}$
B. $y = x^{2}$与$y=(x - 1)^{2}$
C. $y=\sqrt{x^{2}}$与$y = x$
D. $y = 1$与$y = x^{0}$

答案： BCD

4. 已知函数f(x - 1)=x^{2}+4x - 5，则f(x)的解析式是______________________.

答案： f(x)=x²+6x 解析　f(x-1)=x²+4x-5， 设x-1=t，则x=t+1， 所以f(t)=(t+1)²+4(t+1)-5= t²+6t，故f(x)=x²+6x.

例1 (1)(多选)下列说法中正确的有 ( )
A. $f(x)=\frac{|x|}{x}$与$g(x)=\begin{cases}1,x\geq0, \\-1,x＜0\end{cases}$表示同一个函数
B. 函数$f(x)=\sqrt{x + 1}-\frac{1}{x}$的定义域是[-1，0)∪(0，+∞)
C. $f(x)=x^{2}-2x + 1$与$g(t)=t^{2}-2t + 1$是同一个函数
D. 若$f(x)=|x - 1|-x$，则$f(f(\frac{1}{2}))=0$
(2)(2024·济南检测)已知函数f(x)的定义域为[-2，3]，则函数f(2x - 1)的定义域为________________.

答案：
(1)BC　[对于A,函数∮(x)=$\frac{x|}{x}$ 的定义域 g(x)={(-N8。,00)的U定(0,R函.数两函数的定义域不同，所以不是同一个函数，故A错误;对于B,由题意，在f(x)=$\frac{1}{T}$中，{xx+≠01≥,0.解得x≥-1且x≠0，故B正确;对于 C.函数f(x)=x²-2x+1与g(t)= l²-2t+1的定义域与对应关系都相同，所以两函数是同一个函数，故C正确;对于D.由f(x)=|x-1|-x，可得f($\frac{1}{2}$)=0，所以f(∮($\frac{1}{2}$))= f
(0)=1，故D错误.]
(2)[-$\frac{1}{2}$,2] 解析　由-2≤2x-1≤3,解得-$\frac{1}{2}$ ≤x≤2,所以函数f(2x-1)的定义域为[-$\frac{1}{2}$,2]

跟踪训练1 (1)下列各组函数表示同一个函数的是 ( )
A. $f(x)=\sqrt{x^{2}}$，$g(x)=(\sqrt{x})^{2}$
B. $f(x)=\frac{1}{x}-1$，$g(x)=\frac{1}{x - 1}$
C. $f(x)=\begin{cases}x,x\geq0, \\-x,x＜0\end{cases}$，$g(t)=|t|$
D. $f(x)=x + 1$，$g(x)=\frac{x^{2}-1}{x - 1}$
(2)(2023·衡阳模拟)已知函数f(x)的定义域为[2，8]，则函数$h(x)=f(2x)+\sqrt{9 - x^{2}}$的定义域为 ( )
A. [4，16] B. (-∞，1]∪[3，+∞)
C. [1，3] D. [3，4]

答案：
(1)C　
(2)C

例2 (1)已知f(1 - sin x)=cos^{2}x，求f(x)的解析式；
(2)已知$f(x^{2}+\frac{1}{x^{2}})=x^{4}+\frac{1}{x^{4}}$，求f(x)的解析式；
(3)已知f(x)是一次函数且3f(x + 1)-2f(x - 1)=2x + 17，求f(x)的解析式；
(4)若对任意实数x，均有f(x)-2f(-x)=9x + 2，求f(x)的解析式.

答案： 解　
(1)(换元法)设1-sinx=1，t∈[0,2],则sinx=1-1，
∵f(1-sinx)=cos²x=1-sin²x，
∴f(t)=1-(1-1)²=2t-t²,t∈[0,2]即f(x)=2x-x²(0≤x≤2).
(2)(配法)f(x²+$\frac{1}{x²}$)=x²+$\frac{1}{x}$= (x²+$\frac{1}{x²}$)2-2, 又x²÷$\frac{1}{x²}$≥2(x².$\frac{1}{x²}$=2，当且仅当x²=$\frac{1}{x²}$，即x=±1时等号成立。设t=x²+$\frac{1}{x²}$， 则t≥2,
∴f
(1)=²-2(1≥2),
(3)(待定系数法):f(x)是一次函数，可设f(x)=ax+b(a≠0)，
∴3[a(x+1)+b]-2[a(x-1)+b]=2x+17.
(4)(解方程组法)
∵f(x)-2f(-x) =9x+2,　　　　　　　　　　　　①
∴f(-x)-2f(x)=9(-x)+2，　②由①+2×②得-3f(x)=-9x+6,
∴f(x)=3x-2(x∈R).