《2024年步步高大一轮复习讲义高中数学人教A版》

1.判断下列结论是否正确.（请在括号中打“√”或“×”）
（1）集合$\{x\in\mathbf{N}|x^3 = x\}$，用列举法表示为$\{-1,0,1\}$. （ ）
（2）$\{x|y = x^2 + 1\}=\{y|y = x^2 + 1\}=\{(x,y)|y = x^2 + 1\}$. （ ）
（3）若$1\in\{x^2,x\}$，则$x = -1$或$x = 1$. （ ）
（4）对任意集合$A$，$B$，都有$(A\cap B)\subseteq(A\cup B)$. （ ）

答案：
(1)×　
(2)×　
(3)×　
(4)√

2.（必修第一册P14T4改编）设集合$A = \{x|3\leqslant x\lt7\}$，$B = \{x|2\lt x\lt10\}$，则$(\complement_{\mathbf{R}}A)\cap B$等于（ ）
A.$\{x|2\lt x\leqslant3\}$
B.$\{x|7\lt x\lt10\}$
C.$\{x|2\lt x\lt3$或$7\leqslant x\lt10\}$
D.$\{x|2\lt x\leqslant3$或$7\lt x\lt10\}$

答案： C

3.（必修第一册P35T9改编）已知集合$A = \{1,3,a^2\}$，$B = \{1,a + 2\}$，若$A\cup B = A$，则实数$a = $_______.

答案： 2

4.（必修第一册P9T5改编）已知集合$A = \{x|0\lt x\lt a\}$，$B = \{x|0\lt x\lt2\}$，若$B\subseteq A$，则实数$a$的取值范围为____________.

答案： $[2,+\infty)$

例1（1）（2023·长春模拟）已知集合$A = \{(x,y)|x^2 + y^2 = 4\}$，$B = \{(x,y)|x + y = 0\}$，则$A\cap B$的子集个数为（ ）
A.1 B.2 C.3 D.4

答案：
(1)D ；

（2）已知集合$A = \{0,m,m^2 - 3m + 2\}$，且$2\in A$，则实数$m$的值为（ ）
A.2 B.3 C.0 D.$ - 2$

答案：
(2)B　[因为集合$A = \{0,m,m^2 - 3m + 2\}$，且$2\in A$，则$m = 2$或$m^2 - 3m + 2 = 2$，解得$m\in\{0,2,3\}$.当$m = 0$时，集合$A$中的元素不满足互异性；当$m = 2$时，$m^2 - 3m + 2 = 0$，集合$A$中的元素不满足互异性；当$m = 3$时，$A = \{0,3,2\}$，符合题意。综上所述，$m = 3$.]

跟踪训练1（1）（2023·苏州模拟）设集合$A = \{1,2,3\}$，$B = \{4,5\}$，$C = \{x + y|x\in A,y\in B\}$，则$C$中元素的个数为（ ）
A.3 B.4 C.5 D.6

答案：
(1)B　

（2）若含有3个实数的集合既可表示成$\{a,\frac{b}{a},1\}$，又可表示成$\{a^2,a + b,0\}$，则$a^{2024} + b^{2024} = $_______.

答案：
(2)1

例2（1）（2023·海口质检）已知集合$A = \{x|x\gt5\}$，$B = \{x|1 - \log_2x\lt0\}$，则（ ）
A.$A\subseteq B$ B.$B\subseteq A$
C.$A\cap B = \varnothing$ D.$A\cup B = \mathbf{R}$

答案：
(1)A ；

（2）已知集合$A = \{x|x\lt - 1$或$x\geqslant3\}$，$B = \{x|ax + 1\leqslant0\}$，若$B\subseteq A$，则实数$a$的取值范围是（ ）

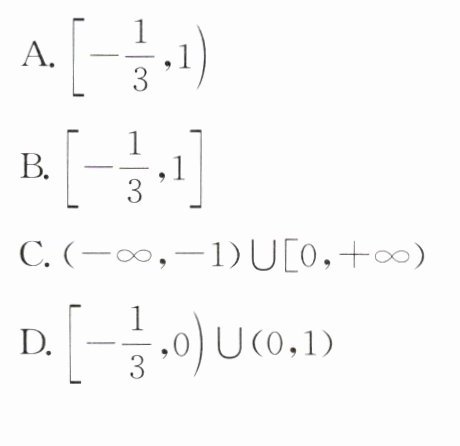
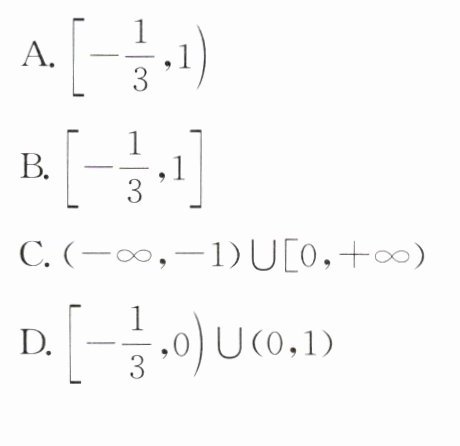
答案：
(2)A　[
∵$B\subseteq A$，
∴①若$B = \varnothing$，即$ax + 1\leqslant0$无解，此时$a = 0$，满足题意。②若$B\neq\varnothing$，即$ax + 1\leqslant0$有解，当$a\gt0$时，可得$x\leqslant-\frac{1}{a}$，要使$B\subseteq A$，$a\gt0$，则需要$\left\{-\frac{1}{a}\lt - 1\right\}$，解得$0\lt a\lt1$；当$a\lt0$时，可得$x\geqslant-\frac{1}{a}$，要使$B\subseteq A$，$a\lt0$，则需要$\left\{-\frac{1}{a}\geqslant3\right\}$，解得$-\frac{1}{3}\leqslant a\lt0$，综上，实数$a$的取值范围是$\left[-\frac{1}{3},1\right)$.

跟踪训练2（1）已知集合$M = \{x|y = \sqrt{1 - x^2},x\in\mathbf{R}\}$，$N = \{x|x = m^2,m\in M\}$，则集合$M$，$N$的关系是（ ）
A.$M\supsetneqq N$ B.$N\supsetneqq M$
C.$M\subseteq\complement_{\mathbf{R}}N$ D.$N\subseteq\complement_{\mathbf{R}}M$

答案：
(1)B ；

（2）设集合$A = \{x| - 1\leqslant x + 1\leqslant6\}$，$B = \{x|m - 1\lt x\lt2m + 1\}$，当$x\in\mathbf{Z}$时，集合$A$的非空真子集的个数为_______；当$B\subseteq A$时，实数$m$的取值范围是____________________.

答案：
(2)254　$\{m|m\leqslant - 2或 - 1\leqslant m\leqslant2\}$