《2024年步步高大一轮复习讲义高中数学人教A版》

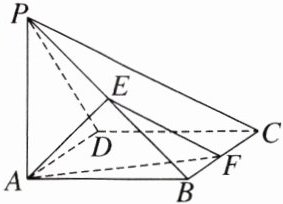
例2 (2024·常州模拟)如图，在四棱锥P - ABCD中，底面ABCD为正方形，PA⊥底面ABCD，PA = AB = 2，E为线段PB的中点，F为线段BC上的动点.
(1)证明：平面AEF⊥平面PBC；
(2)若直线AF与平面PAB所成的角的余弦值为$\frac{2\sqrt{5}}{5}$，求点P到平面AEF的距离.

答案：
方法一　
(1)证明　　因为PA⊥底面ABCD,BCC平面ABCD， 　所因以为四PA边⊥形BACBCD为正方形， 　所以AB⊥BC， 　又因为PA∩AB=A,PA,ABC平面PAB，所以BC⊥平面PAB. 　因为AEC平面PAB，所以AE⊥BC.因为PA=AB，E为线段PB的中点，又所因以为AEP⊥B{EBC=B,PB,BCC二平面PBC,所以AE⊥平面PBC. 　又因为AEC平面AEF, 　所以平面AEF⊥平面PBC. 　
(2)解　　因为PA 　⊥底面ABCD，AB 　⊥AD,以A为坐 　　　　　　　　 标原点，以AB, 　 AD,AP的方向分 　　为x轴、y轴、之 　　的正方向，建立如图所示的空间直坐标系， 　　 A(0.0,0),P(0,0,2),E(1.0,1),知u=(0,1,0)是平面PAB的一个向量， 　设BF=t(t∈[0,2]),则F(2,1,0)，所以AE=(1,0,1),AF=(2,0),所以Icos(AF,u)|=IAF.u|= 　　　　　　　　　　　IAFIIu|$\sqrt{1-(\frac{2\sqrt{5}}{5})}$ 　即$\frac{t}{\sqrt{+4}}$=$\frac{5}{5}$，解得t=1, 所以AF=(2,1，0)， 设n=(x1.y1，2)为平面AEF的法向量，一 则{nn..$\frac{AE}{AF}$二|即{x2xi+1+zy1=1=00，， 令x1=-1，则y1=2，21=1, 所以平面AEF的法向量 n又=因(为-1→A,P2,=1)(，0,0,2), 所以点P到平面AEF的距离为 d=$\frac{IAP.n|}{一n}$=$\frac{2}{6}$=$\frac{\sqrt{6}}{3}$， 所以点P到平面AEF的距离为$\frac{\sqrt{6}}{3}$ 方法二　
(1)证明　　因为PA⊥底面 ABCD.PAC平面PAB, 所以平面PAB⊥底面ABCD, 又平面PAB∩底面ABCD=AB,BC ⊥AB,BCC:平面ABCD， 所以BC⊥平面PAB. 因为AEC平面PAB，所以AE⊥BC.因为PA=AB，E为线段PB的中点，所因为以PABE∩⊥BPCB=B,PB,BCC平面PBC,所以AE⊥平面PBC， 又因为AEC二平面AEF， 所以平面AEF⊥平面PBC.
(2)解　　由
(1)可知，∠BAF是直线 AF与平面PAB所成的角，所以 cos∠BAF=$\frac{AB}{AF}$=$\frac{AB}{\sqrt{AB+BF²}}$=$\frac{25}{5}$,解得BF=$\frac{1}{2}$AB=$\frac{1}{2}$BC=1， 故F是BC的中点. 所以AF=　$\sqrt{AB+BF²}$=√5,AE= $\frac{1}{2}$PB=√2,EF=　$\sqrt{AF²-AE²}$=√3,△AEF的面积为 S△AEF=$\frac{1}{2}$AE.EF=$\frac{√6}{2}$ 因为PA=AB=2,△PAE的面积为S△PAE=$\frac{1}{2}$S△PAB=$\frac{1}{4}$PA.AB=1,设点P到平面AEF的距离为h, 则有V三楼性P-AEF=$\frac{1}{3}$S△AEF.h= $\frac{\sqrt{6}}{6}$h=V三F-PAE=$\frac{1}{3}$S△PAE.BF= $\frac{1}{3}$，解得h=$\frac{\sqrt{6}}{3}$, 所以点P到平面AEF的距离为$\frac{\sqrt{6}}{3}$ 方法三　
(1)证明　　因为PA⊥底面 ABCD,AB⊥AD, 以以$\frac{A}{AB}$,→A坐D标,→A原P点的， 方向分别为x轴、 　　　　　　　　 y轴、之轴的正方 向，建立如图所示的 空间直角坐标系， 则A(0,0,0)，B(2,0,0),C(2,2,0),P(0,0,2),E(1,0,1)， 所设以BFA三Et=(t(∈1[,00,,12])),,则AFF=(2(2,,,|,10,)0,),PB=(2,0,-2),BC=(0,2,0), 设n=(x1.y1,之)为平面A￡F的法向量，一 则{nn..$\frac{AE}{AF}$==00，，所以|2二十“|00.,取y1=2，则x1=-t，21=t， 则n=(-1,2,t)， 　设m=(x2.y2.22)为平面PBC的法→-0　　　2.x2-2文2=0,{m.$\frac{PB}{BC}$=0.所以{2y2=0, 　取x2=1，则y2=0,2=1， 　则m=(1,0,1), 　因为n.m=-+0+t=0，所以n⊥m，所以平面AEF⊥平面PBC 　
(2)解　　易知u=(0,10)是平面PAB的一个法向量， 　所以Icos(AF,u)|=AF.u|= 　　　　　　　　　　　IAF||u|1-($\frac{2\sqrt{5}}{5}$),即$\frac{(}{\sqrt{²²+4}}$=$\frac{\sqrt{5}}{5}$, 　解得t二1;所以n=(-1,2,1). 　又所因以点为APP到=平(0面,0A)E2)F的距离为 　　　→ 　d=$\frac{AP.n|}{|n|}$=$\frac{2}{6}$=$\frac{\sqrt{6}}{3}$, 　所以点P到平面AEF的距离为$\frac{\sqrt{6}}{3}$

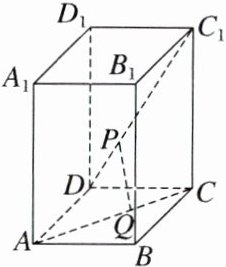
例3 如图，在正四棱柱ABCD - A₁B₁C₁D₁中，AB = BC = 1，AA₁ = 2.动点P，Q分别在线段C₁D，AC上，则线段PQ长度的最小值是 （ ）

A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.1
D.$\frac{4}{3}$

答案：
B　[由题意可知，线段PQ长度的如最小图值所为示异,以面点直线DC为D与AC的距离坐标原点，以DA, 　 DC,DD所在直线 　分别为x,y,2轴建 　　　　　　　　　 立空间直角坐标系， 　则A(1.0,0),C(O, 　1,0),C1(0,1,2), 　 D(0,0.0), 　→D所A以=A(C1.=0.(0-),1,1,0),DC=(0，1,2),设由题n=意(x可,得y,z{nn)满..足$\frac{AC}{DC:}$→n⊥=A-ycx+，n+2⊥zy五==C00,,， 　　　x=y, 　解得{z=一$\frac{y}{2}$, 　取y=2，则x=2,2=-1, 　可得n=(2,2,-1)， 　因此|PQImn=$\frac{IDA.n|}{n}$=$\frac{2}{3}$.]

跟踪训练1（多选）如图，正方体ABCD - A₁B₁C₁D₁的棱长为2，E为棱DD₁的中点，F为棱BB₁的中点，则 （ ）

A.点A₁到直线B₁E的距离为$\frac{2\sqrt{5}}{3}$
B.直线FC₁到直线AE的距离为2
C.点B到平面AB₁E的距离为$\sqrt{2}$
D.直线FC₁到平面AB₁E的距离为$\frac{2}{3}$

答案： AD