《2024年步步高大一轮复习讲义高中数学人教A版》

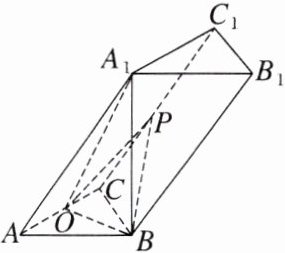
例4 (2023·常德模拟)如图，三棱柱ABC - A₁B₁C₁的底面是等边三角形，平面ABB₁A₁⊥平面ABC，A₁B⊥AB，AC = 2，∠A₁AB = 60°，O为AC的中点.
(1)求证：AC⊥平面A₁BO；
(2)试问线段CC₁上是否存在点P，使得平面POB与平面A₁OB夹角的余弦值为$\frac{2\sqrt{7}}{7}$，若存在，请计算$\frac{CP}{CC_{1}}$的值；若不存在，请说明理由.

答案：

(1)证明
　
∵△ABC是等边三角形，O是AC的中点…
∴AC⊥OB,
　
∵平面ABBA1⊥平面ABC,平面 ABBlA∫平面ABC=AB,A|B⊥ AB,A,BC平面ABBlA,
　
∴A,B⊥平面ABC,
　
∵ACC平面ABC,
∴A,B⊥AC,
　
∵AC⊥OB，ABIVOB=B,A,B,OB C平面A:BO,
∴AC⊥平面A,BO 　
(2)解　　存在， 　线段CCi的中 　点P满足题意 　理由如下: 　　　　　　　 由
(1)得A1B⊥ 　平面ABC， 　OB⊥AC， 　以O为坐标原点,OA.OB，所在直线分别为x轴、y轴，过点O作Oz// A1B，以O2所在直线为之轴，建立如图所示的空间直角坐标系， 　0则),0A((01,.00:,00))，.BA(0(0,$\sqrt{3}$$\sqrt{3}$,0,2),$\sqrt{3}$C)(,-则1$\frac{，0.}{OB}$ 　设=$\frac{0.}{CP}$$\sqrt{3}$=,1$\frac{)，}{CC}$=1t=A(-=1，$\sqrt{3}$,2t,$\sqrt{3}$),t,2$\sqrt{3}$1),0≤1≤1,则$\frac{！}{OP}$=O$\frac{(}{OC}$C+C$\frac{\sqrt{3}}{CP}$P.= (-1-1　$\sqrt{3}$1.2$\sqrt{3}$1), 　易知平面AOB的一个法向量为n= (1.0,0)，设平面POB的法向量为m =(x.y，z), 则mm..→OOPδ==√(-3y1=-01,)x+　　$\sqrt{3}$ty 　　　+2$\sqrt{3}$tz=0， 　{ 取x=2$\sqrt{3}$t,则m=(2$\sqrt{3}$1.0,1+1)，由题意得|cos(n,m)|=$\frac{n.m|}{nllm|}$= $\frac{2\sqrt{3}1}{\sqrt{12r²+(1+1)²}}$=$\frac{2√7}{7}$,
∵0≤t≤1.
∴解得t=$\frac{CP}{CC:}$=$\frac{1}{2}$，
∴线段CC上存在点P,使得平面POB与平面AOB夹角的余弦值为$\frac{2\sqrt{7}}{7}$,此时$\frac{CP}{CC.}$=$\frac{1}{2}$

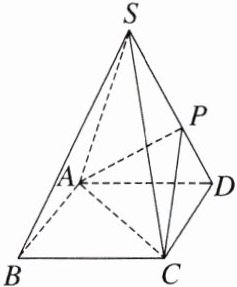
跟踪训练2 如图，四棱锥S - ABCD的底面是正方形，每条侧棱的长都是底面边长的$\sqrt{2}$倍，P为侧棱SD上的点.
(1)求证：AC⊥SD；
(2)若SD⊥平面PAC，求平面PAC与平面DAC夹角的大小；
(3)在(2)的条件下，侧棱SC上是否存在一点E，使得BE//平面PAC.若存在，求SE∶EC的值；若不存在，请说明理由.

答案：

(1)证明　如图，连 接BD交AC于点 0,连接SO. 由题意知，SO⊥平 　　　　　　　　 面ABCD，以O为 坐标原点，以OB， OC.OS所在直线 分别为x轴、y轴、 2轴，建立空间直角坐标系，设底面边长为a，则高SO=$\frac{\sqrt{6}}{2}$a, 于是s(0.0,$\frac{\sqrt{6}}{2}$a)D(-$\frac{\sqrt{2}}{2}$a,0,0)):c(o.$\frac{√2}{2}$a,0). 于是0C=(o,$\frac{2}{2}$a,0), SD=(-$\frac{√2}{2}$a.0.-$\frac{\sqrt{6}}{2}$a)): 则忒.$\frac{2}{SD}$=0，所以OC⊥SD, 故OC⊥SD，从而AC⊥SD
(2)解　　由题设知，平面PAC的一个法向量为DS=($\frac{\sqrt{2}}{2}$a.0.$\frac{\sqrt{6}}{2}$a), 平面DAC的一个法向量为ōs= (0.0.$\frac{\sqrt{6}}{2}$a): 设平面PAC与平面DAC的夹角为0，则cosθ=|COS(OS,DS＞|= I|ōOsSI.IDDsSI1=$\frac{6}{2}$a.$\sqrt{2}$a=$\frac{\sqrt{3}}{2}$: 所以平面PAC与平面DAC夹角的大小为30°.
(3)解　假设在棱SC上存在一点E 使BE//平面PAC. 由
(2)知DS是平面PAC的一个法向量，且DS=($\frac{\sqrt{2}}{2}$a,0,$\frac{\sqrt{6}}{2}$a): ōs=(0,-$\frac{2}{2}$a,$\frac{\sqrt{6}}{2}$a 设CE=CS((0≤t≤1) 因为B($\frac{\sqrt{2}}{2}$a,o.0),c(o,$\frac{\sqrt{2}}{2}$a,0),所以BC=(-$\frac{\sqrt{2}}{2}$a,$\frac{\sqrt{2}}{2}$,0): 则BE=BC+$\frac{2}{CE}$=$\frac{2}{BC}$+ics =(-$\frac{\sqrt{2}}{2}$a,$\frac{\sqrt{2}}{2}$a(1-1),$\frac{\sqrt{6}}{2}$at)): 由BE.DS=0, 得一$\frac{a²}{2}$+0+$\frac{3}{2}$a²t=0，解得t=$\frac{1}{3}$,当SE:EC=2;1时，BE⊥DS. 由于BE平面PAC, 故BE//平面PAC. 因此在棱SC上存在点E,使BE//平面PAC,此时SE:EC=2:1.