第113页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
2.(必修第二册P60T8改编)已知向量$\boldsymbol{m}=(2x,1)$与向量$\boldsymbol{n}=\left(\frac{1}{2},-\frac{1}{2}\right)$垂直,则$x$等于 ( )
A. $\frac{1}{4}$
B. $-\frac{1}{4}$
C. $\frac{1}{2}$
D. $-\frac{1}{2}$
A. $\frac{1}{4}$
B. $-\frac{1}{4}$
C. $\frac{1}{2}$
D. $-\frac{1}{2}$
答案:
C [
∵m=(2x,1)与n=($\frac{1}{2}$,一$\frac{1}{2}$) 垂直,
∴m.n=(2x,1).($\frac{1}{2}$,一$\frac{1}{2}$)= r一$\frac{1}{2}$=0,即x=$\frac{1}{2}$.]
∵m=(2x,1)与n=($\frac{1}{2}$,一$\frac{1}{2}$) 垂直,
∴m.n=(2x,1).($\frac{1}{2}$,一$\frac{1}{2}$)= r一$\frac{1}{2}$=0,即x=$\frac{1}{2}$.]
3.(2023·郑州模拟)已知向量$\boldsymbol{a}$,$\boldsymbol{b}$满足$\vert\boldsymbol{b}\vert = 2\vert\boldsymbol{a}\vert = 2$,且$\boldsymbol{a}$与$\boldsymbol{b}$的夹角为$\frac{2\pi}{3}$,则$(2\boldsymbol{a}+\boldsymbol{b})\cdot\boldsymbol{a}$等于 ( )
A. 12
B. 4
C. 3
D. 1
A. 12
B. 4
C. 3
D. 1
答案:
D [因为|b|=2|a|=2, 所以(2a+b).a=2a²+a.b =2|a|²+|a||b|.cos$\frac{2π}{3}$ =2+2×1×(-$\frac{1}{2}$)=1.]
4.(必修第二册P18例10改编)已知$\boldsymbol{a}=(1,\sqrt{2})$,$\vert\boldsymbol{b}\vert = 2\sqrt{3}$,$\boldsymbol{a}\cdot\boldsymbol{b} = - 3$,则$\boldsymbol{a}$与$\boldsymbol{b}$的夹角为________.
答案:
120° 解析 设a与b的夹角为日, 因为a=(1$\sqrt{2}$),|b|=2$\sqrt{3}$, a▪b=-3, 所以COSθ=$\frac{a▪b}{|a|b|}$=$\frac{-3}{3×2√3}$=一$\frac{1}{2}$,因为0。≤0≤180°,所以θ=120°, 即a与b的夹角为120°.
例1 (1)(2023·安康模拟)已知四边形$ABCD$为平行四边形,$\vert\overrightarrow{AB}\vert=\sqrt{3}$,$\vert\overrightarrow{AD}\vert = 2$,$\overrightarrow{DN}=2\overrightarrow{NC}$,$\overrightarrow{BM}=3\overrightarrow{MC}$,则$\overrightarrow{AM}\cdot\overrightarrow{NM}$等于 ( )
A. 7 B. 1 C. $\frac{3}{4}$ D. $\frac{1}{4}$
(2)在梯形$ABCD$中,$AB// DC$,$AD\perp DC$,$AD = AB = 2DC = 2$,$E$为$BC$的中点,$F$为$AE$的中点,则$\overrightarrow{CF}\cdot\overrightarrow{DF}$等于 ( )
A. $\frac{31}{16}$ B. $\frac{33}{16}$ C. $\frac{35}{16}$ D. $\frac{37}{16}$
A. 7 B. 1 C. $\frac{3}{4}$ D. $\frac{1}{4}$
(2)在梯形$ABCD$中,$AB// DC$,$AD\perp DC$,$AD = AB = 2DC = 2$,$E$为$BC$的中点,$F$为$AE$的中点,则$\overrightarrow{CF}\cdot\overrightarrow{DF}$等于 ( )
A. $\frac{31}{16}$ B. $\frac{33}{16}$ C. $\frac{35}{16}$ D. $\frac{37}{16}$
答案:
(1)D [如$\frac{AM}{BM}$$\frac{1(}{AM}$)1).$\frac{D}{NM}$($\frac{M}{NC}$[如十(逻$\frac{B}{CM}$;) =(AB+$\frac{3}{4}$BC).($\frac{1}{3}$AB-$\frac{1}{4}$BC) =$\frac{1}{3}$AB-$\frac{3}{16}$BC²=$\frac{1}{3}$×3-$\frac{3}{16}$×4 =$\frac{1}{4}$.]
=(AB+$\frac{3}{4}$BC).($\frac{1}{3}$AB-$\frac{1}{4}$BC) =$\frac{1}{3}$AB-$\frac{3}{16}$BC²=$\frac{1}{3}$×3-$\frac{3}{16}$×4 =$\frac{1}{4}$.]
(2)B [以A为坐 标原点,建立如图 标系, 则A(0,0),B(2,0), C(1,2),D(0,2), E($\frac{3}{2}$,1),F($\frac{3}{4}$,$\frac{1}{2}$), 所以CF=(-$\frac{1}{4}$,一$\frac{3}{2}$), DF=($\frac{3}{4}$,一$\frac{3}{2}$), 所以.DF=-$\frac{1}{4}$×$\frac{3}{4}$+(-$\frac{3}{2}$)×(-$\frac{3}{2}$)=$\frac{33}{16}$.]
标系, 则A(0,0),B(2,0), C(1,2),D(0,2), E($\frac{3}{2}$,1),F($\frac{3}{4}$,$\frac{1}{2}$), 所以CF=(-$\frac{1}{4}$,一$\frac{3}{2}$), DF=($\frac{3}{4}$,一$\frac{3}{2}$), 所以.DF=-$\frac{1}{4}$×$\frac{3}{4}$+(-$\frac{3}{2}$)×(-$\frac{3}{2}$)=$\frac{33}{16}$.]
(1)D [如$\frac{AM}{BM}$$\frac{1(}{AM}$)1).$\frac{D}{NM}$($\frac{M}{NC}$[如十(逻$\frac{B}{CM}$;)
 =(AB+$\frac{3}{4}$BC).($\frac{1}{3}$AB-$\frac{1}{4}$BC) =$\frac{1}{3}$AB-$\frac{3}{16}$BC²=$\frac{1}{3}$×3-$\frac{3}{16}$×4 =$\frac{1}{4}$.]
=(AB+$\frac{3}{4}$BC).($\frac{1}{3}$AB-$\frac{1}{4}$BC) =$\frac{1}{3}$AB-$\frac{3}{16}$BC²=$\frac{1}{3}$×3-$\frac{3}{16}$×4 =$\frac{1}{4}$.] (2)B [以A为坐 标原点,建立如图
 标系, 则A(0,0),B(2,0), C(1,2),D(0,2), E($\frac{3}{2}$,1),F($\frac{3}{4}$,$\frac{1}{2}$), 所以CF=(-$\frac{1}{4}$,一$\frac{3}{2}$), DF=($\frac{3}{4}$,一$\frac{3}{2}$), 所以.DF=-$\frac{1}{4}$×$\frac{3}{4}$+(-$\frac{3}{2}$)×(-$\frac{3}{2}$)=$\frac{33}{16}$.]
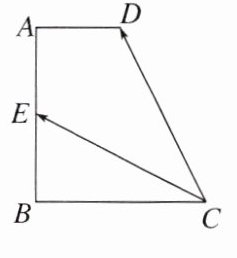
标系, 则A(0,0),B(2,0), C(1,2),D(0,2), E($\frac{3}{2}$,1),F($\frac{3}{4}$,$\frac{1}{2}$), 所以CF=(-$\frac{1}{4}$,一$\frac{3}{2}$), DF=($\frac{3}{4}$,一$\frac{3}{2}$), 所以.DF=-$\frac{1}{4}$×$\frac{3}{4}$+(-$\frac{3}{2}$)×(-$\frac{3}{2}$)=$\frac{33}{16}$.] 跟踪训练1 (1)如图,在直角梯形$ABCD$中,$AD// BC$,$AB\perp BC$,$AB = BC = 2$,$AD = 1$,点$E$在边$AB$上,且$\overrightarrow{CD}\cdot\overrightarrow{CE}=3$,则$BE$等于 ( )
A. 1 B. 2 C. $\frac{1}{2}$ D. $\frac{3}{2}$
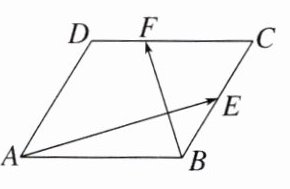
(2)(2023·唐山模拟)如图,在平行四边形$ABCD$中,$AB = 2$,$\angle BAD=\frac{\pi}{3}$,$E$是边$BC$的中点,$F$是$CD$上靠近$D$的三等分点,若$\overrightarrow{AE}\cdot\overrightarrow{BF}=8$,则$\vert\overrightarrow{AD}\vert$等于 ( )
A. 4 B. $4\sqrt{2}$ C. $4\sqrt{3}$ D. 8

A. 1 B. 2 C. $\frac{1}{2}$ D. $\frac{3}{2}$
(2)(2023·唐山模拟)如图,在平行四边形$ABCD$中,$AB = 2$,$\angle BAD=\frac{\pi}{3}$,$E$是边$BC$的中点,$F$是$CD$上靠近$D$的三等分点,若$\overrightarrow{AE}\cdot\overrightarrow{BF}=8$,则$\vert\overrightarrow{AD}\vert$等于 ( )

A. 4 B. $4\sqrt{2}$ C. $4\sqrt{3}$ D. 8
答案:
(1)C
(2)A
(1)C
(2)A
例2 (2023·新高考全国Ⅰ)已知向量$\boldsymbol{a}$,$\boldsymbol{b}$满足$\vert\boldsymbol{a}-\boldsymbol{b}\vert=\sqrt{3}$,$\vert\boldsymbol{a}+\boldsymbol{b}\vert=\vert2\boldsymbol{a}-\boldsymbol{b}\vert$,则$\vert\boldsymbol{b}\vert=$______.
答案:
$\sqrt{3}$ 解析 方法一 因为|a+b|={2a-b|,即(a+b)²=(2a-b)², 则a²+2a▪b+b²=4a²-4a.b+b²,整理得a²-2a▪b=0, 又因为|a-b|=$\sqrt{3}$, 即(a-b)²=3, 则a²-2a▪b+b²=b²=3, 所以1b|=$\sqrt{3}$ 方法二 设C=a-b, 则|c|=$\sqrt{3}$,a+b=c+2b, 2a-b=2c+b, 由题意可得,(C+2b)²=(2c+b)²,则c²+4c.b+4b²=4c²+4c.b+b²,整理得c²=b²,即|b|=|c|=$\sqrt{3}$
例3 (2023·深圳模拟)已知$\boldsymbol{a}$,$\boldsymbol{b}$为单位向量,且$\vert3\boldsymbol{a}-5\boldsymbol{b}\vert = 7$,则$\boldsymbol{a}$与$\boldsymbol{a}-\boldsymbol{b}$的夹角为 ( )
A. $\frac{\pi}{3}$
B. $\frac{2\pi}{3}$
C. $\frac{\pi}{6}$
D. $\frac{5\pi}{6}$
答案:
C [因为a,b为单位向量, 由|3a-5b|=7,所以(3a-5b)²=49 9a-30a▪b+25b²=49, 即9-30a.b+25=49→a▪b=-$\frac{1}{2}$,设a与a-b的夹角为θ, 则cosθ=$\frac{a▪(a-b)}{|a|la-b|}$ =$\frac{a²-a.b}{|a|×\sqrt{(a-b)²}}$ $\frac{1}{2}$ = =$\frac{\sqrt{3}}{2}$, $\frac{1}{2}$ $\frac{(1/2)}{\sqrt{1-2x(-1/2)+1}}$ 又0∈[0,π],所以θ=.]
例4 (2023·新高考全国Ⅰ)已知向量$\boldsymbol{a}=(1,1)$,$\boldsymbol{b}=(1,-1)$,若$(\boldsymbol{a}+\lambda\boldsymbol{b})\perp(\boldsymbol{a}+\mu\boldsymbol{b})$,则 ( )
A. $\lambda+\mu = 1$
B. $\lambda+\mu = - 1$
C. $\lambda\mu = 1$
D. $\lambda\mu = - 1$
答案:
D [因为a=(1,1),b=(1,-1),所以a+xb=(1+λ,1-λ), a+ub=(1+u,1-江), 由(a+λb)⊥(a+μb), 可得(a+λb).(a+μb)=0, 即(1+λ)(1+μ)+(1-λ)(1-μ)=0,整理得xu=-1.]
例5 (1)已知向量$\boldsymbol{a}$与$\boldsymbol{b}$的夹角为$\frac{\pi}{3}$,$\vert\boldsymbol{a}\vert = 2$,$\vert\boldsymbol{b}\vert = 1$,则向量$\boldsymbol{a}$在$\boldsymbol{b}$上的投影向量为 ( )
A. $\boldsymbol{b}$ B. $\frac{1}{2}\boldsymbol{b}$ C. $\boldsymbol{a}$ D. $\frac{1}{2}\boldsymbol{a}$
(2)已知非零向量$\boldsymbol{a}$,$\boldsymbol{b}$满足$\boldsymbol{b}=(\sqrt{3},1)$,$\langle\boldsymbol{a},\boldsymbol{b}\rangle=\frac{\pi}{3}$,若$(\boldsymbol{a}-\boldsymbol{b})\perp\boldsymbol{a}$,则向量$\boldsymbol{a}$在$\boldsymbol{b}$方向上的投影向量的坐标为____________.
答案:
(1)A [由题意知,|a|=2,且向量a与b的夹角为$\frac{π}{3}$, 所以向量a在b上的投影向量为 |a|cos<a,b)$\frac{b}{b|}$=b.]
(2)($\frac{\sqrt{3}}{4}$,$\frac{1}{4}$) 解析 由已知可得, |b|=$\sqrt{(\sqrt{3})+1²}$=2. 因为(a-b)⊥a, 所以(a-b).a=a²-a▪b=|a|²-|a||b|cos=|a|²-|a|=0, 解得|a|=1或|a|=0(舍去)。 量a在b方向上的投影向量为所 = /.$\frac{b}{bl}$ $\frac{1}{4}$b,坐标为($\frac{\sqrt{3}}{4}$,$\frac{1}{4}$).
(1)A [由题意知,|a|=2,且向量a与b的夹角为$\frac{π}{3}$, 所以向量a在b上的投影向量为 |a|cos<a,b)$\frac{b}{b|}$=b.]
(2)($\frac{\sqrt{3}}{4}$,$\frac{1}{4}$) 解析 由已知可得, |b|=$\sqrt{(\sqrt{3})+1²}$=2. 因为(a-b)⊥a, 所以(a-b).a=a²-a▪b=|a|²-|a||b|cos=|a|²-|a|=0, 解得|a|=1或|a|=0(舍去)。 量a在b方向上的投影向量为所 = /.$\frac{b}{bl}$ $\frac{1}{4}$b,坐标为($\frac{\sqrt{3}}{4}$,$\frac{1}{4}$).
查看更多完整答案,请扫码查看


