《2024年步步高大一轮复习讲义高中数学人教A版》

例2 如图,边长为2的等边三角形的外接圆为圆$O$,$P$为圆$O$上任一点,若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则$2x + 2y$的最大值为 （ ）
A. $\frac{8}{3}$ B. 2 C. $\frac{4}{3}$ D. 1

答案：
例2A　[如图，作BC 　的平行线与圆相交 　于点P,与直线AB 　　　　　　　　　 相交于点E,与直线 　 AC相交于点F 　设AP=KE+TAF, 　则λ+=1，
　
∵BC//EF,
∴设$\frac{AE}{AB}$=$\frac{AF}{AC}$=k， 　则ke[0$\frac{4}{3}${, 　十
∴T$\frac{E}{F}$=kλ$\frac{3}{AB}$A$\frac{B.}{AB}$B→+FukA$\frac{k}{AC}$→C,C.→AP=λA→E
∴x=λk，y=mk，
　
∴2.x+2y=2(λ+)k=2k≤$\frac{8}{3}$.]

跟踪训练2 在扇形$OAB$中,$\angle AOB = 60^{\circ}$,$C$为$\overset{\frown}{AB}$上的一个动点,若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则$3x + y$的取值范围是______.

答案： 跟踪训练2[1,3]

例3 已知$O$是$\triangle ABC$内部一点,满足$\overrightarrow{OA}+2\overrightarrow{OB}+m\overrightarrow{OC}=\mathbf{0}$,且$\frac{S_{\triangle AOB}}{S_{\triangle ABC}}=\frac{4}{7}$,则实数$m$等于 （ ）
A. 2 B. 3 C. 4 D. 5

答案： 例3C　[由奔驰定理得$S_{\triangle BOC}\cdot\overrightarrow{OA}+S_{\triangle AOC}\cdot\overrightarrow{OB}+S_{\triangle AOB}\cdot\overrightarrow{OC}=\mathbf{0}$，又$\overrightarrow{OA}+2\overrightarrow{OB}+m\overrightarrow{OC}=\mathbf{0}$，
　
∴$S_{\triangle BOC}:S_{\triangle AOC}:S_{\triangle AOB}=1:2:m$.
∴$\frac{S_{\triangle AOB}}{S_{\triangle ABC}}=\frac{m}{1 + 2 + m}=\frac{4}{7}$， 　解得$m = 4$.] 　

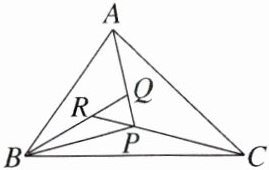
跟踪训练3 已知点$A$,$B$,$C$,$P$在同一平面内,$\overrightarrow{PQ}=\frac{1}{3}\overrightarrow{PA}$,$\overrightarrow{QR}=\frac{1}{3}\overrightarrow{QB}$,$\overrightarrow{RP}=\frac{1}{3}\overrightarrow{RC}$,则$S_{\triangle ABC}:S_{\triangle PBC}$等于 （ ）
A. 14 : 3 B. 19 : 4
C. 24 : 5 D. 29 : 6

答案： 跟踪训练3B　[由$\overrightarrow{QR}=\frac{1}{3}\overrightarrow{QB}$可得$\overrightarrow{PR}-\overrightarrow{PQ}=\frac{1}{3}(\overrightarrow{PB}-\overrightarrow{PQ})$， 　整理可得$\overrightarrow{PR}=\frac{1}{3}\overrightarrow{PB}+\frac{2}{3}\overrightarrow{PQ}$ 　=$\frac{1}{3}\overrightarrow{PB}+\frac{2}{9}\overrightarrow{PA}$， 　由$\overrightarrow{RP}=\frac{1}{3}\overrightarrow{RC}$可得$\overrightarrow{RP}=\frac{1}{3}(\overrightarrow{PC}-\overrightarrow{PR})$，整理可得$\overrightarrow{PR}=-\frac{1}{2}\overrightarrow{PC}$， 　所以$-\frac{1}{2}\overrightarrow{PC}=\frac{1}{3}\overrightarrow{PB}+\frac{2}{9}\overrightarrow{PA}$， 　整理得$4\overrightarrow{PA}+6\overrightarrow{PB}+9\overrightarrow{PC}=\mathbf{0}$， 　由奔驰定理可得$S_{\triangle ABC}:S_{\triangle PBC}=(4 + 6 + 9):4 = 19:4$.]

1. 在$\triangle ABC$中,已知$D$是$AB$边上一点,若$\overrightarrow{CD}=\frac{1}{3}\overrightarrow{CA}+\lambda\overrightarrow{CB}$,则$\lambda$等于 （ ）
A. $\frac{2}{3}$
B. $\frac{1}{3}$
C. $-\frac{1}{3}$
D. $-\frac{2}{3}$

答案： A

2. 已知$\triangle ABC$和点$M$满足$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\mathbf{0}$,若存在实数$m$,使得$\overrightarrow{AB}+\overrightarrow{AC}=m\overrightarrow{AM}$,则$m$等于（ ）
A. 2
B. 3
C. 4
D. 5

答案：
B
∵$\frac{[}{MA}$+法→M一B+(M常C规=方0，法)
∴M为△ABC的重心， 　如图，连接AM并延 　长交BC于D,则D 　为BC的中点， 　　　　　　　　　
∴AM=$\frac{2}{3}$AD 　又AD=$\frac{1}{2}$(AB+AC),
　
∴AM=$\frac{1}{3}$AB+AC), 　即AB+$\frac{3}{AC}$=3AM，
∴m=3. 　方法二　(等和线法) 　 BC是值为1的等和 　线，过M作BC的平 　行线， 　　　　　　　　　 AM=$\frac{1}{m}$AB+$\frac{1}{m}$AC, 　　　 　易知$\frac{AM|}{AD}$=$\frac{2}{3}$,
　
∴$\frac{1}{m}$+$\frac{1}{m}$=$\frac{2}{3}$，
　
∴m=3.

3. 在$\triangle ABC$中,$M$为边$BC$上任意一点,$N$为$AM$的中点,$\overrightarrow{AN}=\lambda\overrightarrow{AB}+\mu\overrightarrow{AC}$,则$\lambda + \mu$的值为 （ ）
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. 1

答案：
A设$\frac{[}{BM}$=法t二BC,(常规方法) 　　TM　$\frac{1}{2}$AM=$\frac{1}{2}$(AB+BM)= 　$\frac{1}{2}$　　　$\frac{t}{2}$BC=$\frac{1}{2}$AB+$\frac{t}{2}$(AC- AB)=($\frac{1}{2}$-$\frac{t}{2}$)AB+$\frac{t}{2}$AC,
　
∴λ=$\frac{1}{2}$-$\frac{t}{2}$u=$\frac{t}{2}$,
∴λ+μ=$\frac{1}{2}$:方法二　(等和线法) 　如图，BC为值是1 　的等和线，过N作 　　　　　　　　　 BC的平行线，设λ十 　u=k，则k= 　　　　　　 　　　　　　 　由图易知，$\frac{IANI}{IAM|}$=$\frac{1}{2}$, 　即λ+=k=$\frac{1}{2}$.]

4. 点$P$在$\triangle ABC$内部,满足$\overrightarrow{PA}+2\overrightarrow{PB}+3\overrightarrow{PC}=\mathbf{0}$,则$S_{\triangle ABC}:S_{\triangle APC}$为 （ ）
A. 2 : 1
B. 3 : 2
C. 3 : 1
D. 5 : 3

答案： C　[根据奔驰定理得，$S_{\triangle PBC}:S_{\triangle PAC}:S_{\triangle PAB}=1:2:3$，所以$S_{\triangle ABC}:S_{\triangle APC}=3:1$.]

5. 如图,$\triangle BCD$与$\triangle ABC$的面积之比为2,点$P$是区域$ABDC$内的任一点(含边界),且$\overrightarrow{AP}=\lambda\overrightarrow{AB}+\mu\overrightarrow{AC}$,则$\lambda + \mu$的取值范围是 （ ）

A. [0,1]
B. [0,2]
C. [0,3]
D. [0,4]

答案：
C　[如图，过点P作GH//BC,分别交AC，　　的延长线于点G，H，设 AP=x$\frac{A}{AG}$+yAH,则x+y=1，当点P位于点D时，G，H分别位于点C',点B' 　　　　

∵△BCD与△ABC的面积之比为2:1,
∴
∴$\frac{AC}{AP}$AACP'=x3A4ACCC',+AyBAA'=B;3AB,→ 　=3xAC+3yAB=λAB+UAC,
　
∴λ=3y,=3x→入+μ=3x+3y=3.当点P位于A点时，显然有　　　=0,综上，λ十μ的取值范围是[0大.3].]

6. 已知点$C$为扇形$AOB$的弧$\overset{\frown}{AB}$上任意一点,且$\angle AOB = 120^{\circ}$,若$\overrightarrow{OC}=\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}$($\lambda,\mu\in\mathbf{R}$),则$\lambda + \mu$的取值范围是 （ ）
A. [-2,2]
B. (1,$\sqrt{2}$]
C. [1,$\sqrt{2}$]
D. [1,2]

答案：
D　[方法一　(常规方法) 　设圆O的半径为1,由已知可设OB 为x轴的正半轴，0为坐标原点，建立直角坐标系(图略)，其中A(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$), ni　　θ) 　{其(中1B0x,θ(o,{){ 　有āC=OA+OB(λ,∈R), 　即(cos0,sin0))=λ(($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)+u(1,0),整理得一$\frac{1}{2}$λ+丝=cosθ，$\frac{\sqrt{3}}{2}$λ=sinθ，解得λ=$\frac{2sinθ}{\sqrt{3}}$u=cos0+$\frac{sinθ}{\sqrt{3}}$, 　则λ+u=2√si3nθ÷cos0+$\frac{sinθ}{\sqrt{3}}$=√3sinθ+oosθ=2siin(0+玄),θ∈[0,$\frac{2π}{3}${， 　易得λ+u∈[1,2]. 　方法二(等和线法) 　设λ+μ=k， 　如图，当C位于点A 　或点B时，A,B,C三 　　　　　　　　　　 点共线， 　所以k=λ+u=1, 　当点C运动到AB的 　中点时，k=λ+=2， 　所以λ+u∈[1,2].]

7. 如图所示,在$\triangle ABC$中,$D$,$F$分别是$AB$,$AC$的中点,$BF$与$CD$交于点$O$,设$\overrightarrow{AB}=\boldsymbol{a}$,$\overrightarrow{AC}=\boldsymbol{b}$,向量$\overrightarrow{AO}=\lambda\boldsymbol{a}+\mu\boldsymbol{b}$,则$\lambda + \mu$的值为______.

答案： $\frac{2}{3}$

8. 已知$O$是面积为4的$\triangle ABC$内部一点,且有$\overrightarrow{OA}+\overrightarrow{OB}+2\overrightarrow{OC}=\mathbf{0}$,则$\triangle AOC$的面积为______.

答案：
1 　解析　　方法一　　如 　图，设AC的中点为 　M因.为B$\frac{C}{A}$+中→O点B+为2aN0→C. 　　　　　　　　　 =ōA+OC+OB+ 　ōc=0, 　所以2OM+2ON=0, 　即OM+ON=0, 　所以O为线段MN的中点， 　所以S△ACC=$\frac{1}{2}$S△ANC=$\frac{1}{2}$×$\frac{1}{2}$S△ABC =$\frac{1}{2}$×$\frac{1}{2}$×4=1. 　方法二　　因为ōA+OB+2OC=0，根据奔驰定理可得， 　S△BOC:S△AOC:S△AOB=1:1:2, 　所以$\frac{SAOC}{SABC}$=$\frac{1}{1+1+2}$=$\frac{1}{4}$， 　又S△ABC=4，所以S△AOC=1.

9. 设点$O$在$\triangle ABC$的内部,且$\overrightarrow{AB}=4\overrightarrow{OB}+5\overrightarrow{OC}$,则$S_{\triangle OAB}$与$S_{\triangle OBC}$之比是______.

答案： 5 　 A解整O析理+可O得B由$\frac{4}{OA}$A烹+=B34O$\frac{5}{OB}$ōBB++5,5O0ōCCC=变0形,可得根据奔驰定理可得 　S△OBC:S△OAC:S△OAB=1:3:5, 　则$\frac{SOAB}{SOBC}$==5.

10. 在正六边形$ABCDEF$中,$P$是$\triangle CDE$内(包括边界)的动点,设$\overrightarrow{AP}=\alpha\overrightarrow{AB}+\beta\overrightarrow{AF}$($\alpha,\beta\in\mathbf{R}$),则$\alpha + \beta$的取值范围是______________.

答案：
[3,4] 　解析　　如图,直线 　 BF为k=1的等和 　线，当P在△CDE 　　　　　　　　　 内(包括边界)时，直 　线EC是最近的等 　和线,过D点的等和 　线是最远的，所以α+B∈$\frac{AD}{AM}$:设正六边形的边长为2,则AN=3， AM=1,AD=4, 　故α+β∈[3,4].