《2024年步步高大一轮复习讲义高中数学人教A版》

跟踪训练2 (1) 如图，在山脚A处测得山顶P的仰角为37°，沿坡角为23°的斜坡向上走28 m到达B处，在B处测得山顶P的仰角为53°，且A，B，P，C，Q在同一平面，则山的高度约为(参考数据：sin 37°≈0.6) （ ）

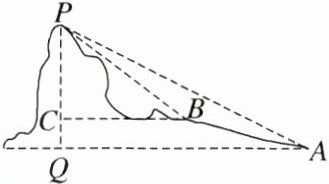
A. 30 m B. 32 m C. 34 m D. 36 m
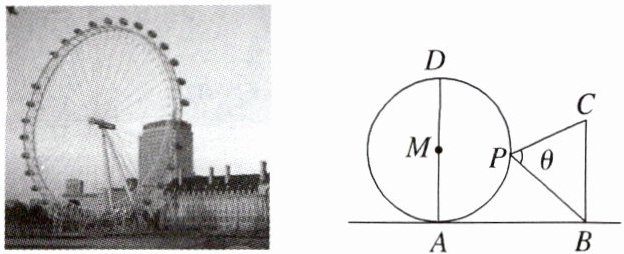
(2) “伦敦眼”坐落在英国伦敦泰晤士河畔，是世界上首座观景摩天轮，又称“千禧之轮”，该摩天轮的半径为6(单位：10 m)，游客在乘坐舱P升到上半空鸟瞰伦敦建筑BC，伦敦眼与建筑之间的距离AB为12(单位：10 m)，游客在乘坐舱P看建筑BC的视角为θ. 当乘坐舱P在伦敦眼的最高点D时，视角θ = 30°，则建筑BC的高度为______________.(单位：10 m)

答案：
(1)A 　
(2)12$\sqrt{3}$-12

例3 已知在岛A南偏西38°方向，距岛A 3海里的B处有一艘救援艇. 岛A处的一艘故障船正以10海里/小时的速度向岛A北偏西22°方向行驶，问救援艇朝何方向以多大速度行驶，恰好用0.5小时追赶上该故障船?
(参考数据：sin 38°取$\frac{5\sqrt{3}}{14}$，sin 22°取$\frac{3\sqrt{3}}{14}$)

答案：
解　　如图，设救 　援艇在C处追赶上 　故障船,D为岛A正 　　　　　　　　　　 南方向上一点，救援 　艇的速度为x海里/ 　小时， 　结合题意知BC= 　0.5x，AC=5,∠BAC=180°-38°-22°=120°, 　由余弦定理可得BC²=AB+AC²-2AB.ACcos120°=9+25-2×3×5 x(-$\frac{1}{2}$)=49， 　所以BC=0.5x=7，解得x=14. 　又由正弦定理得sin∠ABC= 　　　　　　　　　　$\frac{\sqrt{3}}{2}$ 　$\frac{AC.sinBAC}{BC}$=$\frac{2}{7}$=$\frac{5\sqrt{3}}{14}$, 　所以∠ABC=38°, 　又∠BAD=38°，所以BC//AD， 　故救援艇以14海里/小时的速度向正北方向行驶，恰好用0.5小时追赶上该故障船

跟踪训练3 (1) (2023·南京模拟) 如图所示，在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°，向山顶前进100 m到达B处，又测得C对于山坡的斜度为45°，若CD = 50 m，山坡对于地平面的坡度为θ，则cos θ等于（ ）

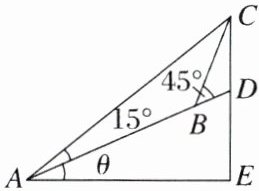
A. $\frac{\sqrt{3}}{3}$ B. $\sqrt{6}$ - 2
C. $\sqrt{3}$ - 1 D. $\sqrt{2}$ - 1
(2) 甲船在A处观察乙船，乙船在它北偏东60°方向，相距a海里的B处，乙船向正北方向行驶，若甲船速度是乙船速度的$\sqrt{3}$倍，甲船为了尽快追上乙船，朝北偏东θ方向前进，则θ = ______.

答案：

(1)C　　[在△ABC中，∠ACB=180°-∠BAC-∠ABC= 　180°-15°-135°=30°， 　由正弦定理知$\frac{BC}{sinBAC}$=$\frac{AB}{sinACB}$, 　　　　　　　　　　　100×$\frac{\sqrt{6}√2}{4}$ 　故BC=$\frac{AB.sinBAC}{sinACB}$= 　　　　　　　　　　　　　$\frac{1}{2}$ 　=50　$\sqrt{6}$-$\sqrt{2}$), 　在△BDC中，$\frac{BC}{sinBDC}$=$\frac{CD}{sinDBC}$，故5s0i(n√∠6B-D√C2)=$\frac{50}{2}$, 　　　　　　　　2

∴sin∠BDC=$\sqrt{3}$-1, 　　即sin(θ+90°)=$\sqrt{3}$-1, 　　即cosθ=$\sqrt{3}$-1.] 　　
(2)30° 　　解析　如图,设两船在 　　 C处相遇， 　　则由题意得∠ABC= 　　180°--60°=120°, 　　　　　　　　　　　　 且$\frac{AC}{BC}$=√3， 　　由正弦定理得$\frac{AC}{BC}$= 　　$\frac{sin120}{sinBAC}$=$\sqrt{3}$, 　　所以sin∠BAC=$\frac{1}{2}$ 　　又因为O°＜∠BAC＜60°, 　　所所以以∠日=BA60C°-=3300。°=30°.