《2025年课堂精练九年级数学上册北师大版大庆专版》

一般地,点C把线段AB分成两条线段AC和BC(如图4-4-25所示),如果$\frac{AC}{AB}=\frac{BC}{AC}$,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.

答案： $\frac{AC}{AB}=\frac{BC}{AC}$；黄金分割点；黄金比

1. 点P是线段AB的黄金分割点(AP＞BP),则$\frac{BP}{AP}=$$\frac{\sqrt{5}-1}{2}$.

答案： $\frac{\sqrt{5}-1}{2}$

2. 已知点P是线段AB的黄金分割点,且PA＞PB. 若AB= 10,则AP= $5\sqrt{5}-5$.

答案： $5\sqrt{5}-5$

3. 如图4-4-26,若点P是AB的黄金分割点,则线段AP,PB,AB满足的关系式是$\frac{AP}{AB}=\frac{PB}{AP}$.

答案： $\frac{AP}{AB}=\frac{PB}{AP}$

4. 如图4-4-27,点P是线段AB的黄金分割点,且AP＞BP. 设以AP为边的正方形的面积为$S_1$,以PB为宽,以AB为长的矩形的面积为$S_2$,试比较$S_1与S_2$的大小.

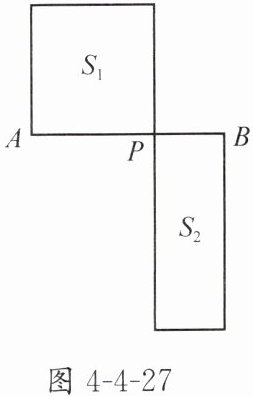
答案： $S_{1}=S_{2}$.

1. 黄金比是多少？

答案： 黄金比是$\dfrac{\sqrt{5}-1}{2}$，其近似值为$0.618$。

2. 一条线段有几个黄金分割点？

答案： 答题卡：
2.
解：一条线段有两个黄金分割点。
设线段AB，若点C把线段AB分成两条线段AC和BC(AC＞BC)，如果$\frac{AC}{AB}=\frac{BC}{AC}$，那么称线段AB被点C黄金分割，点C叫做线段AB的黄金分割点。
同理，在线段AB上另一点D（D与C不重合），若满足$\frac{BD}{AB}=\frac{AD}{BD}$，点D也是线段AB的黄金分割点。
所以一条线段有两个黄金分割点。

探究一：黄金分割
如图4-4-28,C为线段AB上一点.

问题1：测量线段AC,BC的长度,AC=$\sqrt{5}-1$,BC=$3 - \sqrt{5}$.
问题2：$\frac{AC}{AB}= $$\frac{\sqrt{5}-1}{2}$,$\frac{BC}{AC}= $$\frac{\sqrt{5}-1}{2}$.
问题3：$\frac{AC}{AB}与\frac{BC}{AC}$的值相等吗？
归纳总结：点C把线段AB分成两条线段AC和BC,如果$\frac{AC}{AB}=\frac{BC}{AC}$,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比,其中$\frac{AC}{AB}= $$\frac{\sqrt{5}-1}{2}$≈0.618.
思考：一条线段的黄金分割点有几个？
2个

答案： 设$AB = 2$，通过测量（或根据黄金分割定义构造计算）可得：
问题 1：$AC=\sqrt{5}-1$，$BC = 2 - (\sqrt{5}-1)=3 - \sqrt{5}$。
问题 2：$\frac{AC}{AB}=\frac{\sqrt{5}-1}{2}$，$\frac{BC}{AC}=\frac{3 - \sqrt{5}}{\sqrt{5}-1}=\frac{\sqrt{5}-1}{2}$。
问题 3：$\frac{AC}{AB}$与$\frac{BC}{AC}$的值相等。
归纳总结：点$C$把线段$AB$分成两条线段$AC$和$BC$，如果$\frac{AC}{AB}=\frac{BC}{AC}$，那么称线段$AB$被点$C$黄金分割，点$C$叫做线段$AB$的黄金分割点，$AC$与$AB$的比叫做黄金比，其中$\frac{AC}{AB}=\frac{\sqrt{5}-1}{2}\approx0.618$。
思考：一条线段的黄金分割点有$2$个。