第117页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
探究二:多边形缩小时位似中心与相似比
如图 4-8-15,在平面直角坐标系中,四边形 $ABCD$的坐标分别是 $A(-8,6)$,$B(2,-2)$,$C(6,5)$,$D(4,8)$. 回答下列问题:

问题 1:将点 $A$,$B$,$C$,$D$ 的横坐标、纵坐标都乘$\frac{1}{2}$,得到四个点 $A_1$,$B_1$,$C_1$,$D_1$,作出四边形 $A_1B_1C_1D_1$,四边形 $A_1B_1C_1D_1$与四边形 $ABCD$位似吗?如果位似,指出位似中心和相似比,并指出两个四边形位于位似中心的同侧还是两侧.
问题 2:将点 $A$,$B$,$C$,$D$ 的横坐标、纵坐标都乘$-\frac{1}{2}$,得到四个点 $A_2$,$B_2$,$C_2$,$D_2$,作出四边形 $A_2B_2C_2D_2$,你发现了什么?
归纳总结:
如图 4-8-15,在平面直角坐标系中,四边形 $ABCD$的坐标分别是 $A(-8,6)$,$B(2,-2)$,$C(6,5)$,$D(4,8)$. 回答下列问题:

问题 1:将点 $A$,$B$,$C$,$D$ 的横坐标、纵坐标都乘$\frac{1}{2}$,得到四个点 $A_1$,$B_1$,$C_1$,$D_1$,作出四边形 $A_1B_1C_1D_1$,四边形 $A_1B_1C_1D_1$与四边形 $ABCD$位似吗?如果位似,指出位似中心和相似比,并指出两个四边形位于位似中心的同侧还是两侧.
问题 2:将点 $A$,$B$,$C$,$D$ 的横坐标、纵坐标都乘$-\frac{1}{2}$,得到四个点 $A_2$,$B_2$,$C_2$,$D_2$,作出四边形 $A_2B_2C_2D_2$,你发现了什么?
归纳总结:
在位似变换中,如果坐标乘以一个非零常数 $k$,原图形与变换后的图形位似,位似中心为坐标原点,相似比为 $|k|$。如果 $k$ 为正,原图形与变换后的图形位于位似中心的同侧;如果 $k$ 为负,原图形与变换后的图形位于位似中心的两侧。
答案:
问题 1:
解:
点 $A_1$ 的坐标为 $(-8 × \frac{1}{2}, 6 × \frac{1}{2}) = (-4, 3)$。
点 $B_1$ 的坐标为 $(2 × \frac{1}{2}, -2 × \frac{1}{2}) = (1, -1)$。
点 $C_1$ 的坐标为 $(6 × \frac{1}{2}, 5 × \frac{1}{2}) = (3, 2.5)$。
点 $D_1$ 的坐标为 $(4 × \frac{1}{2}, 8 × \frac{1}{2}) = (2, 4)$。
四边形 $A_1B_1C_1D_1$ 与四边形 $ABCD$ 的对应点连线都经过同一点 $O(0,0)$,因此四边形 $A_1B_1C_1D_1$ 与四边形 $ABCD$ 位似,位似中心为坐标原点 $O(0,0)$,相似比为 $\frac{1}{2}$,两个四边形位于位似中心的同侧。
问题 2:
解:
点 $A_2$ 的坐标为 $(-8 × -\frac{1}{2}, 6 × -\frac{1}{2}) = (4, -3)$。
点 $B_2$ 的坐标为 $(2 × -\frac{1}{2}, -2 × -\frac{1}{2}) = (-1, 1)$。
点 $C_2$ 的坐标为 $(6 × -\frac{1}{2}, 5 × -\frac{1}{2}) = (-3, -2.5)$。
点 $D_2$ 的坐标为 $(4 × -\frac{1}{2}, 8 × -\frac{1}{2}) = (-2, -4)$。
四边形 $A_2B_2C_2D_2$ 与四边形 $ABCD$ 的对应点连线也都经过同一点 $O(0,0)$,因此四边形 $A_2B_2C_2D_2$ 与四边形 $ABCD$ 位似,位似中心为坐标原点 $O(0,0)$,相似比为 $\frac{1}{2}$,但两个四边形位于位似中心的两侧。
归纳总结:
在位似变换中,如果坐标乘以一个非零常数 $k$,原图形与变换后的图形位似,位似中心为坐标原点,相似比为 $|k|$。如果 $k$ 为正,原图形与变换后的图形位于位似中心的同侧;如果 $k$ 为负,原图形与变换后的图形位于位似中心的两侧。
解:
点 $A_1$ 的坐标为 $(-8 × \frac{1}{2}, 6 × \frac{1}{2}) = (-4, 3)$。
点 $B_1$ 的坐标为 $(2 × \frac{1}{2}, -2 × \frac{1}{2}) = (1, -1)$。
点 $C_1$ 的坐标为 $(6 × \frac{1}{2}, 5 × \frac{1}{2}) = (3, 2.5)$。
点 $D_1$ 的坐标为 $(4 × \frac{1}{2}, 8 × \frac{1}{2}) = (2, 4)$。
四边形 $A_1B_1C_1D_1$ 与四边形 $ABCD$ 的对应点连线都经过同一点 $O(0,0)$,因此四边形 $A_1B_1C_1D_1$ 与四边形 $ABCD$ 位似,位似中心为坐标原点 $O(0,0)$,相似比为 $\frac{1}{2}$,两个四边形位于位似中心的同侧。
问题 2:
解:
点 $A_2$ 的坐标为 $(-8 × -\frac{1}{2}, 6 × -\frac{1}{2}) = (4, -3)$。
点 $B_2$ 的坐标为 $(2 × -\frac{1}{2}, -2 × -\frac{1}{2}) = (-1, 1)$。
点 $C_2$ 的坐标为 $(6 × -\frac{1}{2}, 5 × -\frac{1}{2}) = (-3, -2.5)$。
点 $D_2$ 的坐标为 $(4 × -\frac{1}{2}, 8 × -\frac{1}{2}) = (-2, -4)$。
四边形 $A_2B_2C_2D_2$ 与四边形 $ABCD$ 的对应点连线也都经过同一点 $O(0,0)$,因此四边形 $A_2B_2C_2D_2$ 与四边形 $ABCD$ 位似,位似中心为坐标原点 $O(0,0)$,相似比为 $\frac{1}{2}$,但两个四边形位于位似中心的两侧。
归纳总结:
在位似变换中,如果坐标乘以一个非零常数 $k$,原图形与变换后的图形位似,位似中心为坐标原点,相似比为 $|k|$。如果 $k$ 为正,原图形与变换后的图形位于位似中心的同侧;如果 $k$ 为负,原图形与变换后的图形位于位似中心的两侧。
【例 1】如图 4-8-16,$E(-4,2)$,$F(-1,-1)$,以 $O$ 为位似中心,按相似比 $1:2$,把$\triangle EFO$缩小,则点 $E$ 的对应点 $E'$ 的坐标为(
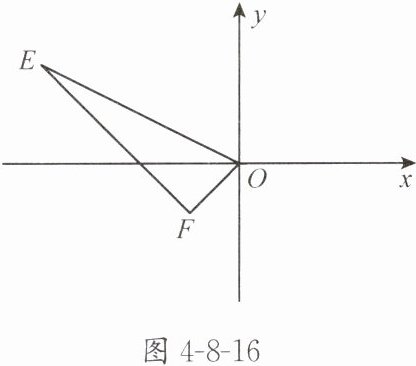
A.$(2,-1)或(-2,1)$
B.$(2,-1)$
C.$(8,-4)或(-8,4)$
D.$(8,-4)$
A
).
A.$(2,-1)或(-2,1)$
B.$(2,-1)$
C.$(8,-4)或(-8,4)$
D.$(8,-4)$
答案:
A
【例 2】如图 4-8-17,在平面直角坐标系中,有四个点:$A(0,1)$,$B(4,1)$,$C(5,4)$,$D(1,4)$.
(1)顺次连接点 $A$,$B$,$C$,$D$,$A$,得到一个怎样的四边形?
(2)将各点的横坐标、纵坐标都乘 2,得到点 $A'$,$B'$,$C'$,$D'$,那么四边形 $A'B'C'D'$ 是什么图形,它与四边形 $ABCD$ 有何关系?
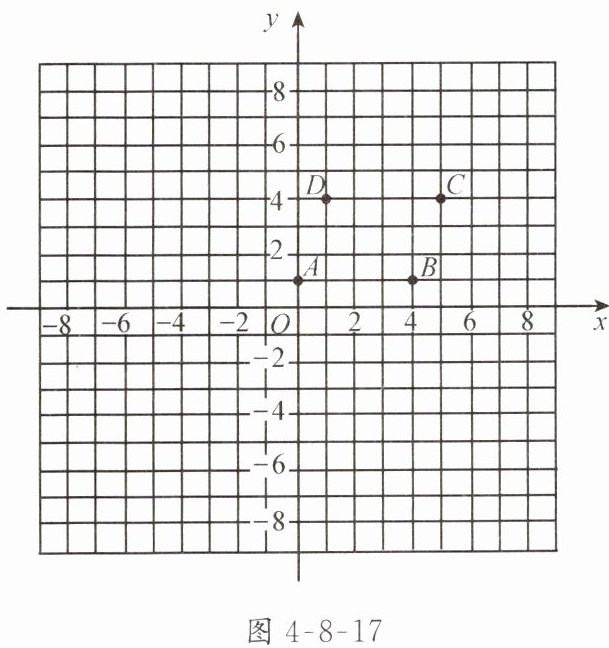
(1)顺次连接点 $A$,$B$,$C$,$D$,$A$,得到一个怎样的四边形?
(2)将各点的横坐标、纵坐标都乘 2,得到点 $A'$,$B'$,$C'$,$D'$,那么四边形 $A'B'C'D'$ 是什么图形,它与四边形 $ABCD$ 有何关系?

答案:
(1)平行四边形.
(2)平行四边形,位似.
(1)平行四边形.
(2)平行四边形,位似.
查看更多完整答案,请扫码查看


