《2025年课堂精练九年级数学上册北师大版大庆专版》

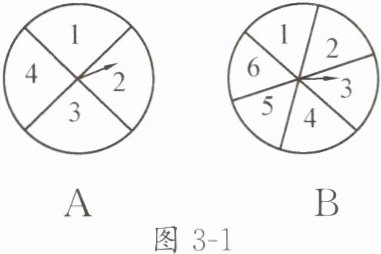
【例 4】如图 3 - 1 是两个相同的且可以自由转动的转盘 $ A $,$ B $. 转盘 $ A $ 被均匀分成 $ 4 $ 等份,分别标上数字 $ 1 $,$ 2 $,$ 3 $,$ 4 $；转盘 $ B $ 被均匀分成 $ 6 $ 等份,分别标上数字 $ 1 $,$ 2 $,$ 3 $,$ 4 $,$ 5 $,$ 6 $. 有人为甲、乙两人设计了一个游戏,其规则如下：
(1)同时转动转盘 $ A $ 与 $ B $.
(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止),把所指的两个数字相乘：如果所得的积是偶数,那么甲胜；如果所得的积是奇数,那么乙胜.
你认为这样的规则是否公平? 请说明理由. 如果不公平,请设计一个公平的规则,并说明理由.
]

答案： 解:这样的规则不公平.
∵P(奇)=$\frac{1}{4}$,P(偶)=$\frac{3}{4}$,
∴P(偶)＞P(奇)，
∴这样的规则不公平，
　　　新规则:
(1)同时转动转盘A和B
(2)转盘停止后，指针各指向一个数字(如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止),把所指的两个数字相加:如果得到的和是偶数，那么甲胜;如果得到的和是奇数，那么乙胜理由:
∵P(奇)=$\frac{1}{2}$,P(偶)=$\frac{1}{2}$,
∴P(偶)=P(奇),
∴新规则公平.(规则不唯一)

1. 从含有 $ 4 $ 个次品的 $ 1000 $ 个螺钉中任取 $ 1 $ 个,它是次品的概率是$\frac{1}{250}$.

答案： $\frac{1}{250}$

2. 一个书架有上、下两层,其中上层有 $ 2 $ 本语文书和 $ 1 $ 本数学书,下层有 $ 2 $ 本语文书和 $ 2 $ 本数学书. 现从上、下两层各随机抽取 $ 1 $ 本,则抽到的 $ 2 $ 本都是数学书的概率为$\frac{1}{6}$.

答案： $\frac{1}{6}$

3. 某中学九(1)班 $ 50 $ 名学生的年龄情况如下表：

从该班随机抽取一人,抽到学生的年龄恰好是 $ 15 $ 岁的概率是$\frac{2}{5}$.

答案： $\frac{2}{5}$

4. 小华用如图 3 - 2 所示的长方体来代替正方体骰子,利用列表法求出掷两次长方体骰子出现的数字相同的概率为 $ \dfrac{1}{6} $,你同意他的做法吗? 为什么?
]

答案： 不同意。长方体骰子各面不均匀，每个面出现的可能性不相等，不满足等可能事件条件，不能用列表法按等可能结果计算概率，故结论错误。