第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
1. 方程 $ mx^{2}-3x= x^{2}-mx+2 $ 是一元二次方程,则 $ m $ 应满足的条件为
m≠1
.
答案:
m≠1
2. 关于 $ x $ 的方程 $ (m+2)x^{|m|}+4x+3m+1= 0 $,当 $ m= $
2
时,它是一元二次方程;当 $ m= $-2
时,它是一元一次方程.
答案:
2;-2
探究一:一元二次方程的定义
一元二次方程的一般形式是
一元二次方程的一般形式是
$ax^{2} + bx + c = 0$(其中 $a \neq 0$)
,二次项系数是$a$
,一次项系数是$b$
,常数项是$c$
.
答案:
答题卡:
一元二次方程的一般形式是 $ax^{2} + bx + c = 0$(其中 $a \neq 0$);
二次项系数是 $a$;
一次项系数是 $b$;
常数项是 $c$。
一元二次方程的一般形式是 $ax^{2} + bx + c = 0$(其中 $a \neq 0$);
二次项系数是 $a$;
一次项系数是 $b$;
常数项是 $c$。
探究二:列一元二次方程
一块矩形铁皮长 30 cm、宽 20 cm,从它的四角各截去一个小正方形,再把四边折起来做成一个无盖的盒子. 若这个盒子的底面积恰好为原铁皮面积的 $ \frac{1}{2} $,列出关于盒子的高 $ x(cm) $ 的方程.
一块矩形铁皮长 30 cm、宽 20 cm,从它的四角各截去一个小正方形,再把四边折起来做成一个无盖的盒子. 若这个盒子的底面积恰好为原铁皮面积的 $ \frac{1}{2} $,列出关于盒子的高 $ x(cm) $ 的方程.
答案:
(30-2x)(20-2x)=30×20×$\frac{1}{2}$.
【例】将 $ (x+1)(4x-5)= 1 $ 化成一元二次方程的一般形式,并求出此时二次项系数、一次项系数和常数项的和.
答案:
答案不唯一,如$(x+1)(4x-5)=1$
$4x^{2}-5x+4x-5=1$
$4x^{2}-x-6=0$
二次项系数为$4$,一次项系数为$-1$,常数项为$-6$
$4+(-1)+(-6)=-3$
$4x^{2}-x-6=0$,$-3$
$4x^{2}-5x+4x-5=1$
$4x^{2}-x-6=0$
二次项系数为$4$,一次项系数为$-1$,常数项为$-6$
$4+(-1)+(-6)=-3$
$4x^{2}-x-6=0$,$-3$
把下列方程化为一元二次方程的一般形式,并写出它们的二次项系数、一次项系数和常数项.
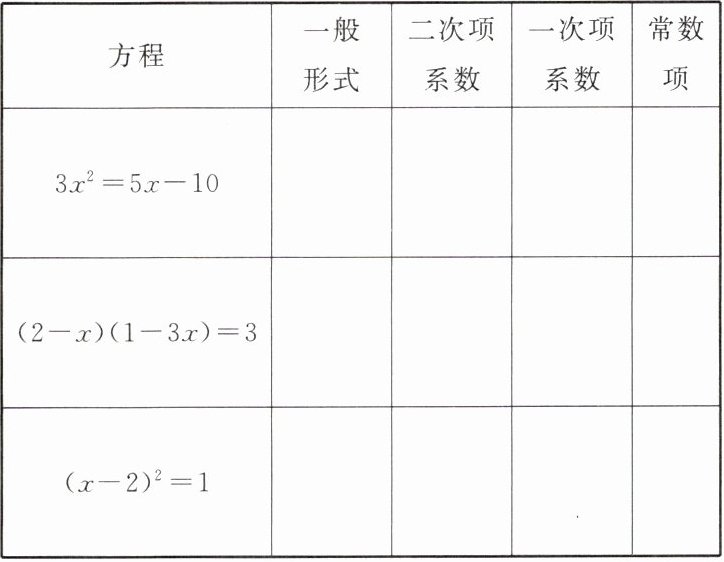

方程一:$3x^2 = 5x - 10$
一般形式:$3x^2 - 5x + 10 = 0$
二次项系数:$3$
一次项系数:$-5$
常数项:$10$
方程二:$(2 - x)(1 - 3x) = 3$
展开整理:
$\begin{aligned}(2 - x)(1 - 3x) &= 3 \\2(1) + 2(-3x) - x(1) + x(3x) &= 3 \\2 - 6x - x + 3x^2 &= 3 \\3x^2 - 7x + 2 - 3 &= 0 \\3x^2 - 7x - 1 &= 0\end{aligned}$
一般形式:$3x^2 - 7x - 1 = 0$
二次项系数:$3$
一次项系数:$-7$
常数项:$-1$
方程三:$(x - 2)^2 = 1$
展开整理:
$\begin{aligned}(x - 2)^2 &= 1 \\x^2 - 4x + 4 &= 1 \\x^2 - 4x + 3 &= 0\end{aligned}$
一般形式:$x^2 - 4x + 3 = 0$
二次项系数:$1$
一次项系数:$-4$
常数项:$3$
表格形式汇总:
| 方程 | 一般形式 | 二次项系数 | 一次项系数 | 常数项 |
|-----------------------|------------------------|------------|------------|--------|
| $3x^2 = 5x - 10$ | $3x^2 - 5x + 10 = 0$ | $3$ | $-5$ | $10$ |
| $(2 - x)(1 - 3x) = 3$| $3x^2 - 7x - 1 = 0$ | $3$ | $-7$ | $-1$ |
| $(x - 2)^2 = 1$ | $x^2 - 4x + 3 = 0$ | $1$ | $-4$ | $3$ |
一般形式:$3x^2 - 5x + 10 = 0$
二次项系数:$3$
一次项系数:$-5$
常数项:$10$
方程二:$(2 - x)(1 - 3x) = 3$
展开整理:
$\begin{aligned}(2 - x)(1 - 3x) &= 3 \\2(1) + 2(-3x) - x(1) + x(3x) &= 3 \\2 - 6x - x + 3x^2 &= 3 \\3x^2 - 7x + 2 - 3 &= 0 \\3x^2 - 7x - 1 &= 0\end{aligned}$
一般形式:$3x^2 - 7x - 1 = 0$
二次项系数:$3$
一次项系数:$-7$
常数项:$-1$
方程三:$(x - 2)^2 = 1$
展开整理:
$\begin{aligned}(x - 2)^2 &= 1 \\x^2 - 4x + 4 &= 1 \\x^2 - 4x + 3 &= 0\end{aligned}$
一般形式:$x^2 - 4x + 3 = 0$
二次项系数:$1$
一次项系数:$-4$
常数项:$3$
表格形式汇总:
| 方程 | 一般形式 | 二次项系数 | 一次项系数 | 常数项 |
|-----------------------|------------------------|------------|------------|--------|
| $3x^2 = 5x - 10$ | $3x^2 - 5x + 10 = 0$ | $3$ | $-5$ | $10$ |
| $(2 - x)(1 - 3x) = 3$| $3x^2 - 7x - 1 = 0$ | $3$ | $-7$ | $-1$ |
| $(x - 2)^2 = 1$ | $x^2 - 4x + 3 = 0$ | $1$ | $-4$ | $3$ |
答案:
方程一:$3x^2 = 5x - 10$
一般形式:$3x^2 - 5x + 10 = 0$
二次项系数:$3$
一次项系数:$-5$
常数项:$10$
方程二:$(2 - x)(1 - 3x) = 3$
展开整理:
$\begin{aligned}(2 - x)(1 - 3x) &= 3 \\2(1) + 2(-3x) - x(1) + x(3x) &= 3 \\2 - 6x - x + 3x^2 &= 3 \\3x^2 - 7x + 2 - 3 &= 0 \\3x^2 - 7x - 1 &= 0\end{aligned}$
一般形式:$3x^2 - 7x - 1 = 0$
二次项系数:$3$
一次项系数:$-7$
常数项:$-1$
方程三:$(x - 2)^2 = 1$
展开整理:
$\begin{aligned}(x - 2)^2 &= 1 \\x^2 - 4x + 4 &= 1 \\x^2 - 4x + 3 &= 0\end{aligned}$
一般形式:$x^2 - 4x + 3 = 0$
二次项系数:$1$
一次项系数:$-4$
常数项:$3$
表格形式汇总:
| 方程 | 一般形式 | 二次项系数 | 一次项系数 | 常数项 |
|-----------------------|------------------------|------------|------------|--------|
| $3x^2 = 5x - 10$ | $3x^2 - 5x + 10 = 0$ | $3$ | $-5$ | $10$ |
| $(2 - x)(1 - 3x) = 3$| $3x^2 - 7x - 1 = 0$ | $3$ | $-7$ | $-1$ |
| $(x - 2)^2 = 1$ | $x^2 - 4x + 3 = 0$ | $1$ | $-4$ | $3$ |
一般形式:$3x^2 - 5x + 10 = 0$
二次项系数:$3$
一次项系数:$-5$
常数项:$10$
方程二:$(2 - x)(1 - 3x) = 3$
展开整理:
$\begin{aligned}(2 - x)(1 - 3x) &= 3 \\2(1) + 2(-3x) - x(1) + x(3x) &= 3 \\2 - 6x - x + 3x^2 &= 3 \\3x^2 - 7x + 2 - 3 &= 0 \\3x^2 - 7x - 1 &= 0\end{aligned}$
一般形式:$3x^2 - 7x - 1 = 0$
二次项系数:$3$
一次项系数:$-7$
常数项:$-1$
方程三:$(x - 2)^2 = 1$
展开整理:
$\begin{aligned}(x - 2)^2 &= 1 \\x^2 - 4x + 4 &= 1 \\x^2 - 4x + 3 &= 0\end{aligned}$
一般形式:$x^2 - 4x + 3 = 0$
二次项系数:$1$
一次项系数:$-4$
常数项:$3$
表格形式汇总:
| 方程 | 一般形式 | 二次项系数 | 一次项系数 | 常数项 |
|-----------------------|------------------------|------------|------------|--------|
| $3x^2 = 5x - 10$ | $3x^2 - 5x + 10 = 0$ | $3$ | $-5$ | $10$ |
| $(2 - x)(1 - 3x) = 3$| $3x^2 - 7x - 1 = 0$ | $3$ | $-7$ | $-1$ |
| $(x - 2)^2 = 1$ | $x^2 - 4x + 3 = 0$ | $1$ | $-4$ | $3$ |
1. 下列方程是一元二次方程的是(
A.$ y= x^{2}-1 $
B.$ x^{2}= 6 $
C.$ x^{2}+5x-1= x^{2}+1 $
D.$ 2(x+1)= 2 $
B
).A.$ y= x^{2}-1 $
B.$ x^{2}= 6 $
C.$ x^{2}+5x-1= x^{2}+1 $
D.$ 2(x+1)= 2 $
答案:
B
2. 将方程 $ 3x^{2}= -6x+8 $ 化为一元二次方程的一般形式后,二次项系数、一次项系数、常数项可能为
①3,6,8;②-3,-6,8;③3,-6,8;④3,6,-8.
②④
.①3,6,8;②-3,-6,8;③3,-6,8;④3,6,-8.
答案:
②④
查看更多完整答案,请扫码查看


