《2025年课堂精练九年级数学上册北师大版大庆专版》

探究一：比例的性质
填空：(1)若 $\frac{a}{b}= \frac{3}{5}$,则 $\frac{a + b}{b}$ 的值是$\frac{8}{5}$.
(2)若 $3x - 4y = 0$,则 $\frac{x}{y}=$$\frac{4}{3}$,$\frac{x + y}{y}=$$\frac{7}{3}$.
(3)若 $x:y:z = 3:5:7$,则 $\frac{2x - 3y + 4z}{5x + 3y - z}$ 的值为$\frac{19}{23}$.

答案：
(1)$\frac{8}{5}$
(2)$\frac{4}{3}$;$\frac{7}{3}$
(3)$\frac{19}{23}$

探究二：黄金三角形
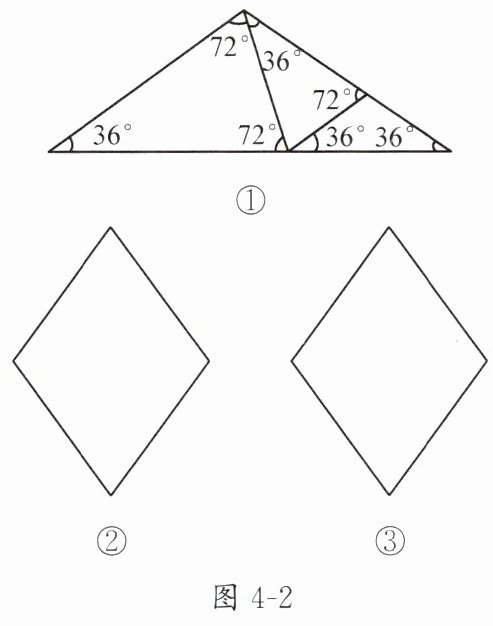
顶角为 $36^{\circ}$ 的等腰三角形称为黄金三角形. 如图 4 - 2①是一个底角为 $36^{\circ}$ 的等腰三角形,我们可以用图示的分割方法继续下去,可以得到若干个黄金三角形. 现有锐角为 $72^{\circ}$ 的菱形(如图 4 - 2②、图 4 - 2③),你能仿照以上的分割方法作出黄金三角形吗？(请在图 4 - 2②、图 4 - 2③中画出符合条件的两种分割方法)

答案： 分割方法一（图②）：
在锐角为72°的菱形中，取一个钝角顶点（内角108°），连接该顶点与对边上一点，使连线长度等于菱形边长。
例：设菱形ABCD，∠B=108°（钝角），在边AD上取点F，使BF=AB（菱形边长），连接BF。则△ABF为黄金三角形（顶角∠ABF=36°，AB=BF，底角∠A=∠AFB=72°）。
分割方法二（图③）：
在锐角为72°的菱形中，取另一个钝角顶点（内角108°），连接该顶点与另一对边上一点，使连线长度等于菱形边长。
例：设菱形ABCD，∠D=108°（钝角），在边AB上取点G，使DG=AD（菱形边长），连接DG。则△ADG为黄金三角形（顶角∠ADG=36°，AD=DG，底角∠A=∠AGD=72°）。

探究三：正方形铁片的面积
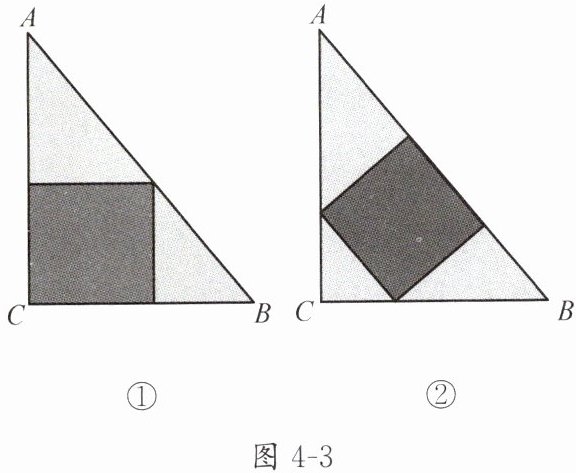
如图 4 - 3,直角三角形铁片 $ABC$ 的两条直角边 $BC,AC$ 的长分别是 $3$ 和 $4$,分别采用图 4 - 3①②两种方法,剪出一块正方形铁片,剪下的正方形铁片的面积哪个较大？请说明理由.

答案： 解:题图4-3①剪下的正方形铁片的面积较大.理由：
题图4-3①中正方形的两条边与直角三角形的两条直角边重合，有一个顶点在斜边上，用相似比求得正方形的边长是$\frac{12}{7}$;题图4-3②中正方形的一条边与直角三角形的斜边重合，有两个顶点在两条直角边上，用相似比求得正方形的边长是$\frac{60}{37}$.因为$\frac{12}{7}=\frac{60}{35}＞\frac{60}{37}$,所以题图4-3①剪下的正方形铁片的面积较大.

探究四：辅助线的作法
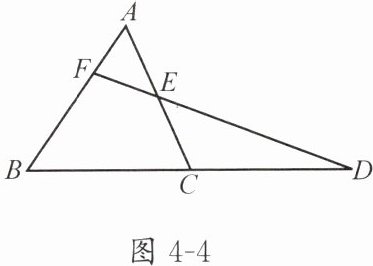
如图 4 - 4,在 $\triangle ABC$ 中,$AE = CE,BC = CD$. 求证：$ED = 3EF$.

答案： 证明:过点C作CH//AB交DE于点H，
∴∠A=∠ECH.
∵∠AEF=∠CEH,AE=CE，
∴△AEF≌△CEH(ASA).
∴EF=EH.
∵BC=CD,CH//AB，
∴CH为△BFD的中位线.
∴H为DF的中点.
∴HF=HD.
∴HD=HF=2EF.
∴ED=HE+HD=EF+2EF=3EF.

1. 已知 $\frac{a}{b}= \frac{c}{d}= \frac{e}{f}= \frac{2}{3}(b + f\neq 0)$,则 $\frac{a + e}{b + f}= $$\frac{2}{3}$.

答案： $\frac{2}{3}$

2. 已知 $(x - 4):2 = x:3$,则 $x= $12.

答案： 12

3. 如图 4 - 5,$DE$ 与 $\triangle ABC$ 的边 $AB,AC$ 分别相交于 $D,E$ 两点,且 $DE// BC$. 若 $DE = 2cm,BC = 3cm,EC= \frac{2}{3}cm$,则 $AC= $2 $cm$.

答案： 2

4. 如图 4 - 6,电灯 $P$ 在横杆 $AB$ 的正上方,$AB$ 在灯光下的影子为 $CD,AB// CD$,$AB = 2m,CD = 5m$,点 $P$ 到 $CD$ 的距离是 $3m$,则点 $P$ 到 $AB$ 的距离是______$\frac{6}{5}$m.zyjl.cn/pic18/2025-09-04/a55861592f753e88ee8c525f0c27627f.jpg?x-oss-process=image/crop,x_1423,y_2262,w_311,h_239">

答案： $\frac{6}{5}$m