第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
探究二:探索验证
1. 如图 4-3-3,两个正六边形的边长分别为 $a$ 和 $b$,它们相似吗?为什么?

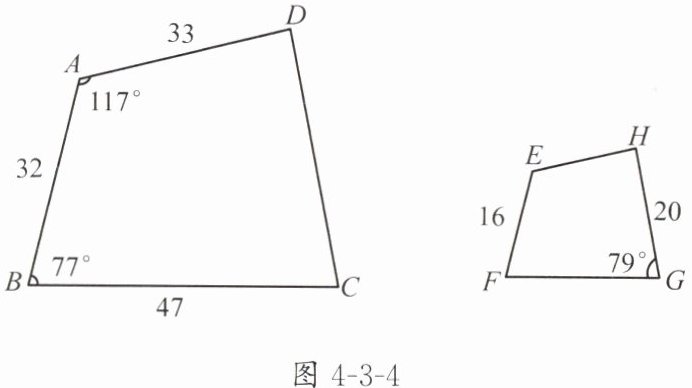
2. 在如图 4-3-4 所示的相似四边形中,你还能求出哪些边和角?试试看.
归纳总结:相似多边形的对应角
1. 如图 4-3-3,两个正六边形的边长分别为 $a$ 和 $b$,它们相似吗?为什么?

2. 在如图 4-3-4 所示的相似四边形中,你还能求出哪些边和角?试试看.

归纳总结:相似多边形的对应角
相等
,对应边成比例
.
答案:
相等;成比例
【例 1】(1)观察下面两组图形,图 4-3-5①中的两个图形相似吗?图 4-3-5②中的两个图形呢?为什么?

(2)如果两个多边形不相似,那么它们的各角可能对应相等吗?它们的各边可能对应成比例吗?

(2)如果两个多边形不相似,那么它们的各角可能对应相等吗?它们的各边可能对应成比例吗?
答案:
1. (1)
对于图$4 - 3 - 5$①:
解:图$4 - 3 - 5$①中的两个图形不相似。
理由:正方形的四个角都是$90^{\circ}$,菱形的角有钝角和锐角(菱形的对角相等,邻角互补),所以它们的角不对应相等。虽然正方形边长$a = 10$,菱形边长$b = 12$,但相似多边形需要满足对应角相等且对应边成比例,这里对应角不相等,所以不相似。
对于图$4 - 3 - 5$②:
解:图$4 - 3 - 5$②中的两个图形不相似。
理由:正方形的边长$a = 10$,矩形的长$b = 12$,宽$c = 8$。正方形的四条边都相等,矩形的对边相等。$\frac{10}{12}\neq\frac{10}{8}$,即对应边不成比例(正方形四个角是$90^{\circ}$,矩形四个角也是$90^{\circ}$,虽然角对应相等,但相似多边形需要角对应相等且边对应成比例,这里边不对应成比例)。
2. (2)
解:
如果两个多边形不相似,它们的各角可能对应相等。例如,正方形(边长为$a$)和矩形(长为$a$,宽为$b$,$a\neq b$),它们的角都对应相等(都是$90^{\circ}$),但因为边不对应成比例($\frac{a}{a}\neq\frac{a}{b}$($b\neq a$)),所以不相似。
如果两个多边形不相似,它们的各边可能对应成比例。例如,菱形(边长为$a$,角为$60^{\circ}$和$120^{\circ}$)和正方形(边长为$a$),$\frac{a}{a}=\frac{a}{a}$,边对应成比例,但角不对应相等(菱形角不是$90^{\circ}$),所以不相似。
综上,(1)图$4 - 3 - 5$①不相似,因为对应角不相等;图$4 - 3 - 5$②不相似,因为对应边不成比例;(2)两个多边形不相似时,各角可能对应相等,各边可能对应成比例。
对于图$4 - 3 - 5$①:
解:图$4 - 3 - 5$①中的两个图形不相似。
理由:正方形的四个角都是$90^{\circ}$,菱形的角有钝角和锐角(菱形的对角相等,邻角互补),所以它们的角不对应相等。虽然正方形边长$a = 10$,菱形边长$b = 12$,但相似多边形需要满足对应角相等且对应边成比例,这里对应角不相等,所以不相似。
对于图$4 - 3 - 5$②:
解:图$4 - 3 - 5$②中的两个图形不相似。
理由:正方形的边长$a = 10$,矩形的长$b = 12$,宽$c = 8$。正方形的四条边都相等,矩形的对边相等。$\frac{10}{12}\neq\frac{10}{8}$,即对应边不成比例(正方形四个角是$90^{\circ}$,矩形四个角也是$90^{\circ}$,虽然角对应相等,但相似多边形需要角对应相等且边对应成比例,这里边不对应成比例)。
2. (2)
解:
如果两个多边形不相似,它们的各角可能对应相等。例如,正方形(边长为$a$)和矩形(长为$a$,宽为$b$,$a\neq b$),它们的角都对应相等(都是$90^{\circ}$),但因为边不对应成比例($\frac{a}{a}\neq\frac{a}{b}$($b\neq a$)),所以不相似。
如果两个多边形不相似,它们的各边可能对应成比例。例如,菱形(边长为$a$,角为$60^{\circ}$和$120^{\circ}$)和正方形(边长为$a$),$\frac{a}{a}=\frac{a}{a}$,边对应成比例,但角不对应相等(菱形角不是$90^{\circ}$),所以不相似。
综上,(1)图$4 - 3 - 5$①不相似,因为对应角不相等;图$4 - 3 - 5$②不相似,因为对应边不成比例;(2)两个多边形不相似时,各角可能对应相等,各边可能对应成比例。
【例 2】如图 4-3-6,矩形的草坪长 20 m、宽 10 m,草坪四周外围有宽 1 m 的环形小路,小路的内外边缘所成的矩形相似吗?为什么?


答案:
不相似,对应边不成比例.
1. 给出下面四个图案:不等边三角形、等边三角形、正方形和矩形. 其中每个图案花边的宽度都相同,那么每个图案中花边的内外边缘所围成的几何图形不一定相似的个数是(

A.4
B.3
C.2
D.1
D
).
A.4
B.3
C.2
D.1
答案:
D
2. 若$\triangle ABC\backsim\triangle DEF$,$AB = 3$,$DE = 4$,$\angle A = 30^{\circ}$,则$\angle D= $
$30^{\circ}$
,$\triangle ABC与\triangle DEF$的相似比为$\frac{3}{4}$
.
答案:
$30^{\circ}$;$\frac{3}{4}$
3. 如果$\triangle ABC$的三条边的长度之比为 $3:5:6$,与其相似的$\triangle A'B'C'$的最长边长 9 cm,且$\triangle A'B'C'与\triangle ABC$的相似比为 2,那么$\triangle ABC$的最短边长
$\frac{9}{4}$ cm
.
答案:
$\frac{9}{4}$ cm
查看更多完整答案,请扫码查看


