第127页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
5. 如图 5-1-5,A,B 在一条直线上,小明从点 A 出发沿 AB 方向匀速前进,4 s 后走到点 D,此时他(CD)在某一灯光下的影长为 AD,继续沿 AB 方向以同样的速度匀速前进 4 s 后到点 F,此时他(EF)的影长为 2 m,然后他再沿 AB 方向以同样的速度匀速前进 2 s 后到达点 H,此时他(GH)处于灯光正下方.
(1)请在图中画出光源 O 点的位置,并画出他位于点 F 时在这个灯光下的影长 FM(不写画法);
(2)求小明沿 AB 方向匀速前进的速度.

(1)请在图中画出光源 O 点的位置,并画出他位于点 F 时在这个灯光下的影长 FM(不写画法);
(2)求小明沿 AB 方向匀速前进的速度.

答案:
解:
(1)如图.

(2)设速度为x(x>0)m/s.根据题意,得CG//AH.
∴△COG∽△AOH.
∴$\frac{CG}{AH}=\frac{OG}{OH}$,即$\frac{OG}{OH}=\frac{6x}{10x}=\frac{3}{5}$.
又
∵CG//AH,
∴△EOG∽△MOH.
∴$\frac{EG}{MH}=\frac{OG}{OH}$,即$\frac{2x}{2+2x}=\frac{3}{5}$.
∴$x=\frac{3}{2}$.
答:小明沿AB方向匀速前进的速度为$\frac{3}{2}$m/s.
解:
(1)如图.

(2)设速度为x(x>0)m/s.根据题意,得CG//AH.
∴△COG∽△AOH.
∴$\frac{CG}{AH}=\frac{OG}{OH}$,即$\frac{OG}{OH}=\frac{6x}{10x}=\frac{3}{5}$.
又
∵CG//AH,
∴△EOG∽△MOH.
∴$\frac{EG}{MH}=\frac{OG}{OH}$,即$\frac{2x}{2+2x}=\frac{3}{5}$.
∴$x=\frac{3}{2}$.
答:小明沿AB方向匀速前进的速度为$\frac{3}{2}$m/s.
1. 如图,夜间小明在路灯下由甲处走到乙处,他在地面上的影子(
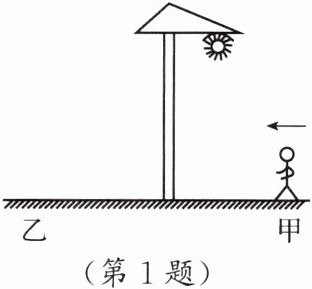
A.先变长后变短
B.先变短后变长
C.逐渐变短
D.逐渐变长
B
).
A.先变长后变短
B.先变短后变长
C.逐渐变短
D.逐渐变长
答案:
B
2. 在平面直角坐标系内,一点光源位于 A(0,5)处,线段 CD⊥x 轴,D 为垂足,C(3,1),则 CD 在 x 轴上的影长为
0.75
,点 C 在 x 轴上的影子的坐标为(3.75,0)
.
答案:
0.75;(3.75,0)
3. 如图,花丛中有一路灯杆 AB. 在灯光下,小明在 D 点处的影长 DE= 3 m,沿 BD 方向行走到达 G 点,DG= 5 m,这时小明的影长 GH= 5 m. 如果小明的身高为 1.7 m,求路灯杆 AB 的高度.(结果精确到 0.1 m)
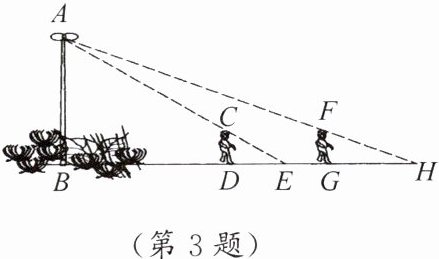

答案:
约6.0 m.
4. 与一盏路灯相对,有一玻璃幕墙,幕墙前面的地面上有一盆花和一棵树. 晚上,幕墙反射路灯灯光形成了那盆花的影子(如图所示),树影是路灯灯光形成的. 你能确定此时路灯的位置吗?
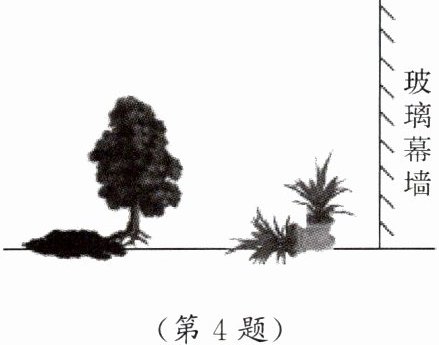

答案:
1. 设花顶端为A,花影顶端为A',连接A与A'并延长,交玻璃幕墙于点O;
2. 延长AO(过点O)至幕墙另一侧,得点S'(路灯在幕墙中的像);
3. 作S'关于玻璃幕墙的对称点S,S即为路灯位置;
4. 验证:设树顶端为B,树影顶端为B',连接B与B',直线BB'过点S,确认S为路灯位置。
结论:按上述步骤确定的点S即为路灯位置。
2. 延长AO(过点O)至幕墙另一侧,得点S'(路灯在幕墙中的像);
3. 作S'关于玻璃幕墙的对称点S,S即为路灯位置;
4. 验证:设树顶端为B,树影顶端为B',连接B与B',直线BB'过点S,确认S为路灯位置。
结论:按上述步骤确定的点S即为路灯位置。
查看更多完整答案,请扫码查看


