第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
3. 如图 4 - 6 - 1,小东设计了两个直角,来测量河宽 DE,他量得 AD = 2 m,BD = 3 m,CE = 9 m,则河宽 DE 为

4 m
.
答案:
4 m
怎样利用相似三角形的有关知识测量旗杆(或高楼或路灯杆或树或烟囱等)的高度?
答案:
方法一:利用阳光下的影子
测量工具:卷尺、标杆(或测人高)
测量数据:人的身高$h$,人的影长$l$,旗杆的影长$L$
相似依据:同一时刻太阳光线平行,人与旗杆均垂直地面,得$\triangle ABC \sim \triangle DEF$($AA$,直角及同位角相等)
比例式:$\frac{h}{H} = \frac{l}{L}$
结论:旗杆高度$H = \frac{hL}{l}$
方法二:利用标杆
测量工具:卷尺、标杆(高度$m$)
测量数据:人眼高度$h$(眼睛到地面距离),人到标杆距离$a$,标杆到旗杆距离$b$,标杆高度$m$
相似依据:过眼睛作水平线交标杆于$G$、旗杆于$H$,得$\triangle EFG \sim \triangle EKH$($AA$,视线平行得同位角相等)
比例式:$\frac{m - h}{H - h} = \frac{a}{a + b}$
结论:旗杆高度$H = h + \frac{(m - h)(a + b)}{a}$
方法三:利用镜子反射
测量工具:卷尺、镜子
测量数据:人的身高$h$,人到镜子距离$l$,旗杆到镜子距离$L$
相似依据:反射角等于入射角,人与旗杆均垂直地面,得$\triangle ABC \sim \triangle DEF$($AA$,直角及反射角等于入射角)
比例式:$\frac{h}{H} = \frac{l}{L}$
结论:旗杆高度$H = \frac{hL}{l}$
测量工具:卷尺、标杆(或测人高)
测量数据:人的身高$h$,人的影长$l$,旗杆的影长$L$
相似依据:同一时刻太阳光线平行,人与旗杆均垂直地面,得$\triangle ABC \sim \triangle DEF$($AA$,直角及同位角相等)
比例式:$\frac{h}{H} = \frac{l}{L}$
结论:旗杆高度$H = \frac{hL}{l}$
方法二:利用标杆
测量工具:卷尺、标杆(高度$m$)
测量数据:人眼高度$h$(眼睛到地面距离),人到标杆距离$a$,标杆到旗杆距离$b$,标杆高度$m$
相似依据:过眼睛作水平线交标杆于$G$、旗杆于$H$,得$\triangle EFG \sim \triangle EKH$($AA$,视线平行得同位角相等)
比例式:$\frac{m - h}{H - h} = \frac{a}{a + b}$
结论:旗杆高度$H = h + \frac{(m - h)(a + b)}{a}$
方法三:利用镜子反射
测量工具:卷尺、镜子
测量数据:人的身高$h$,人到镜子距离$l$,旗杆到镜子距离$L$
相似依据:反射角等于入射角,人与旗杆均垂直地面,得$\triangle ABC \sim \triangle DEF$($AA$,直角及反射角等于入射角)
比例式:$\frac{h}{H} = \frac{l}{L}$
结论:旗杆高度$H = \frac{hL}{l}$
探究一:利用阳光下的影子测量旗杆的高度
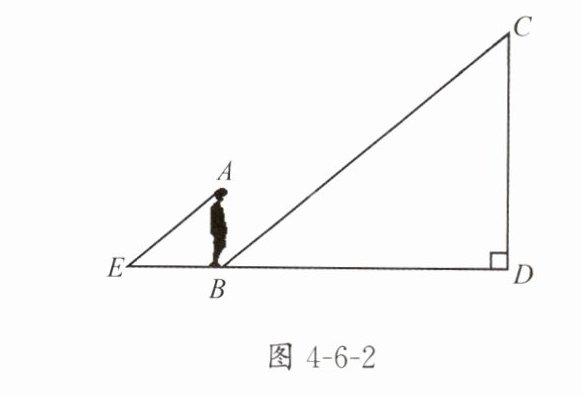
操作方法:选一名同学直立于旗杆影子的顶端处,其他同学测出该同学的影长和同一时刻旗杆的影长.
提示:把太阳的光线看成是平行的.
问题 1:如何证明△ABE∽△CDB?
问题 2:由△ABE∽△CDB 可以得到的比例式是什么?
问题 3:由比例式如何求出旗杆的高度?
归纳总结:只要测量出人的影长
探究二:利用标杆测量旗杆的高度
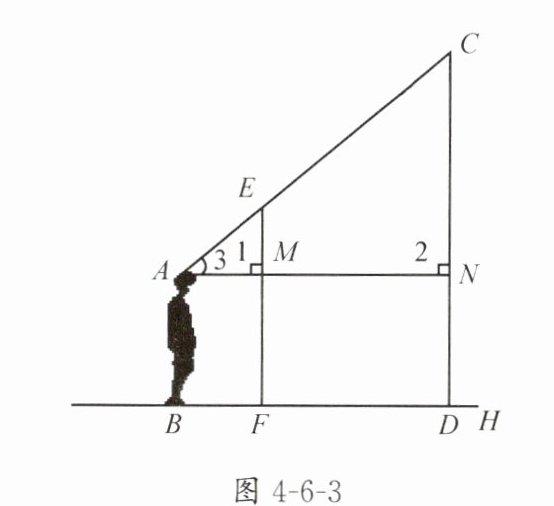
操作方法:选一名同学作为观测者,在观测者与旗杆之间的地面上直立一根高度适当的标杆. 观测者适当调整自己所处的位置,使旗杆的顶端、标杆的顶端与自己的眼睛恰好在一条直线上,这时其他同学立即测出观测者的脚到旗杆底端的距离,以及观测者的脚到标杆底端的距离,然后测出标杆的高,即可求出旗杆的高度.
问题 1:如何证明△AME∽△ANC?
问题 2:由△AME∽△ANC 可以得到的比例式是什么?
问题 3:由比例式如何求出旗杆的高度?
探究三:利用镜子的反射测量旗杆的高度
操作方法:选一名同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记,观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合. 测出此时观测者的脚与镜子的距离,旗杆底部与镜子的距离就能求出旗杆的高度.
提示:入射角= 反射角.
问题 1:需要证明哪两个三角形相似?
问题 2:由两个三角形相似能得到什么比例式?
问题 3:由比例式如何求出旗杆的高度?
归纳总结:
1. 运用方法 1 时可以把太阳光近似地看成
2. 运用方法 2 时观测者的眼睛必须与标杆的顶端和旗杆的顶端
3. 运用方法 3 时应注意光线的

操作方法:选一名同学直立于旗杆影子的顶端处,其他同学测出该同学的影长和同一时刻旗杆的影长.
提示:把太阳的光线看成是平行的.
问题 1:如何证明△ABE∽△CDB?
∵AE//CD(太阳光线平行),∴∠AEB=∠CDB(同位角相等),又∠ABE=∠CDB=90°,∴△ABE∽△CDB(AA)。
问题 2:由△ABE∽△CDB 可以得到的比例式是什么?
AB/CD = EB/DB
问题 3:由比例式如何求出旗杆的高度?
设AB=h(人高),EB=l(人影长),DB=L(旗杆影长),则h/CD=l/L,∴CD=hL/l
归纳总结:只要测量出人的影长
l
,旗杆的影长L
,再知道人的身高h
,就可以求出旗杆H
的高度了.(用字母表示)探究二:利用标杆测量旗杆的高度

操作方法:选一名同学作为观测者,在观测者与旗杆之间的地面上直立一根高度适当的标杆. 观测者适当调整自己所处的位置,使旗杆的顶端、标杆的顶端与自己的眼睛恰好在一条直线上,这时其他同学立即测出观测者的脚到旗杆底端的距离,以及观测者的脚到标杆底端的距离,然后测出标杆的高,即可求出旗杆的高度.
问题 1:如何证明△AME∽△ANC?
∵AM⊥EM,AN⊥CN(水平视线与标杆、旗杆垂直),∴∠AME=∠ANC=90°,又∠MAE=∠NAC(公共角),∴△AME∽△ANC(AA)。
问题 2:由△AME∽△ANC 可以得到的比例式是什么?
AM/AN = EM/CN
问题 3:由比例式如何求出旗杆的高度?
设AM=m(观测者到标杆距离),AN=n(观测者到旗杆距离),EM=a(标杆高-眼高),CN=H - b(旗杆高-眼高,b为眼高),则m/n=a/(H - b),∴H=b + an/m
探究三:利用镜子的反射测量旗杆的高度
操作方法:选一名同学作为观测者,在观测者与旗杆之间的地面上平放一面镜子,在镜子上做一个标记,观测者看着镜子来回移动,直至看到旗杆顶端在镜子中的像与镜子上的标记重合. 测出此时观测者的脚与镜子的距离,旗杆底部与镜子的距离就能求出旗杆的高度.
提示:入射角= 反射角.
问题 1:需要证明哪两个三角形相似?
△ABE∽△CDE
问题 2:由两个三角形相似能得到什么比例式?
AB/CD = BE/DE
问题 3:由比例式如何求出旗杆的高度?
设AB=h(人高),BE=m(观测者到镜子距离),DE=n(旗杆到镜子距离),则h/CD=m/n,∴CD=hn/m
归纳总结:
1. 运用方法 1 时可以把太阳光近似地看成
平行光线
,计算时还要用到观测者的身高
.2. 运用方法 2 时观测者的眼睛必须与标杆的顶端和旗杆的顶端
在一条直线上
,标杆与地面要垂直
,在计算时还要用到观测者的眼睛离地面的高度.3. 运用方法 3 时应注意光线的
入射角
等于反射角
.
答案:
探究一
问题1:
∵AE//CD(太阳光线平行),
∴∠AEB=∠CDB(同位角相等),又∠ABE=∠CDB=90°,
∴△ABE∽△CDB(AA)。
问题2:
AB/CD = EB/DB
问题3:
设AB=h(人高),EB=l(人影长),DB=L(旗杆影长),则h/CD=l/L,
∴CD=hL/l
归纳总结:l,L,h,H
@@探究二
问题1:
∵AM⊥EM,AN⊥CN(水平视线与标杆、旗杆垂直),
∴∠AME=∠ANC=90°,又∠MAE=∠NAC(公共角),
∴△AME∽△ANC(AA)。
问题2:
AM/AN = EM/CN
问题3:
设AM=m(观测者到标杆距离),AN=n(观测者到旗杆距离),EM=a(标杆高-眼高),CN=H - b(旗杆高-眼高,b为眼高),则m/n=a/(H - b),
∴H=b + an/m
@@探究三
问题1:
△ABE∽△CDE
问题2:
AB/CD = BE/DE
问题3:
设AB=h(人高),BE=m(观测者到镜子距离),DE=n(旗杆到镜子距离),则h/CD=m/n,
∴CD=hn/m
归纳总结
1. 平行光线,身高
2. 在一条直线上,垂直
3. 入射角,反射角
问题1:
∵AE//CD(太阳光线平行),
∴∠AEB=∠CDB(同位角相等),又∠ABE=∠CDB=90°,
∴△ABE∽△CDB(AA)。
问题2:
AB/CD = EB/DB
问题3:
设AB=h(人高),EB=l(人影长),DB=L(旗杆影长),则h/CD=l/L,
∴CD=hL/l
归纳总结:l,L,h,H
@@探究二
问题1:
∵AM⊥EM,AN⊥CN(水平视线与标杆、旗杆垂直),
∴∠AME=∠ANC=90°,又∠MAE=∠NAC(公共角),
∴△AME∽△ANC(AA)。
问题2:
AM/AN = EM/CN
问题3:
设AM=m(观测者到标杆距离),AN=n(观测者到旗杆距离),EM=a(标杆高-眼高),CN=H - b(旗杆高-眼高,b为眼高),则m/n=a/(H - b),
∴H=b + an/m
@@探究三
问题1:
△ABE∽△CDE
问题2:
AB/CD = BE/DE
问题3:
设AB=h(人高),BE=m(观测者到镜子距离),DE=n(旗杆到镜子距离),则h/CD=m/n,
∴CD=hn/m
归纳总结
1. 平行光线,身高
2. 在一条直线上,垂直
3. 入射角,反射角
查看更多完整答案,请扫码查看


