《2025年优课堂给力A加九年级数学全一册北师大版》

1. 如图,C是线段AB的黄金分割点,AC＞BC,则下列结论中正确的是(D)

A.$AC^2 + BC^2 = AB^2$
B.$BC \approx 0.618AB$
C.$AC = \frac{\sqrt{5}-1}{2}BC$
D.$BC:AC = AC:AB$

答案： D

2. 如图,已知线段AB,按以下步骤作图：①过点B作BC⊥AB,使$BC = \frac{1}{2}AB$,连接AC；②以点C为圆心,以BC长为半径画弧,交AC于点D；③以点A为圆心,以AD长为半径画弧,交AB于点E. 若$AE = mAB$,则m的值为(A)

A.$\frac{\sqrt{5}-1}{2}$
B.$\frac{\sqrt{5}-2}{2}$
C.$\sqrt{5}-1$
D.$\sqrt{5}-2$

答案： A

3. 已知P是线段AB上的一点,且满足$BP^2 = AP \cdot AB$,如果AB= 10cm,那么BP的长为$ 5\sqrt{5} - 5 $cm.

答案： $ 5\sqrt{5} - 5 $

4. 如图,在△ABC中,AB= AC,∠A= 36°,BD是∠ABC的平分线. 求证：D是线段AC的黄金分割点.
]

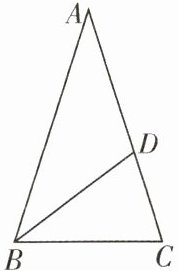
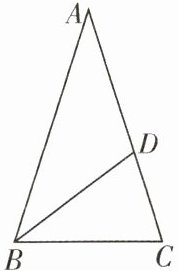
答案： 证明：
∵AB=AC，∠A=36°，
∴∠ABC=∠C=(180°-36°)/2=72°．
∵BD平分∠ABC，
∴∠ABD=∠DBC=72°/2=36°．
∴∠BDC=180°-∠DBC-∠C=180°-36°-72°=72°，
∴∠BDC=∠C，∠A=∠ABD，
∴AD=BD，BD=BC，
∴AD=BC．
∵∠A=∠DBC=36°，∠C=∠C，
∴△ABC∽△BDC，
∴AC/BC=BC/DC．
设AD=BC=x，AC=AB=y，则DC=y-x，
∴y/x=x/(y-x)，
∴x²=y(y-x)，即x²+xy-y²=0，
解得x=(√5-1)y/2（负值舍去），
∴AD=(√5-1)AC/2，
∴D是线段AC的黄金分割点．

5. 唢呐是山西八大套的乐器之一. 如图,一个中号唢呐AB的长约为40cm,若在唢呐上喇叭端的一个黄金分割点P处进行装饰. 则该装饰与吹口的距离AP为(C)

A.$(20\sqrt{5}-20)$cm
B.$(20\sqrt{5}+20)$cm
C.$(60 - 20\sqrt{5})$cm
D.$(40 - 20\sqrt{5})$cm
]

答案： C

6. 研究发现当主持人站在舞台黄金分割点的位置时,视觉声音效果最佳,如图,主持人现站在8m舞台PQ的左边端点P处,那她要站在最佳位置处时至少要走12 - 4√5m.
]

答案： 1. 首先明确黄金分割点的比例关系：
黄金分割比为$\dfrac{\sqrt{5}-1}{2}\approx0.618$。
一条线段$PQ$，若点$M$是线段$PQ$的黄金分割点（$PM\lt MQ$），则$PM = PQ - MQ$，且$MQ=\dfrac{\sqrt{5}-1}{2}PQ$。
2. 然后计算主持人至少走的距离：
已知$PQ = 8m$，主持人从$P$点走到离$P$较近的黄金分割点位置，设该位置为$M$，则$PM=PQ-\dfrac{\sqrt{5}-1}{2}PQ$。
对$PM$进行化简：
$PM = PQ\left(1-\dfrac{\sqrt{5}-1}{2}\right)=PQ×\dfrac{2 - (\sqrt{5}-1)}{2}=PQ×\dfrac{3 - \sqrt{5}}{2}$。
把$PQ = 8$代入上式，得$PM=8×\dfrac{3 - \sqrt{5}}{2}$。
$PM = 12-4\sqrt{5}\approx12 - 4×2.236=12 - 8.944 = 3.056$；
另一种方法：
黄金分割点分线段$PQ$为两段，较长段与全段的比是$\dfrac{\sqrt{5}-1}{2}$，较短段与较长段的比也是$\dfrac{\sqrt{5}-1}{2}$。
较短段$PM=(1 - \dfrac{\sqrt{5}-1}{2})PQ$，$1-\dfrac{\sqrt{5}-1}{2}=\dfrac{2-\sqrt{5} + 1}{2}=\dfrac{3-\sqrt{5}}{2}$，$PM = 8×\dfrac{3-\sqrt{5}}{2}=12 - 4\sqrt{5}\approx12-4×2.24 = 12 - 8.96=3.04$；
也可以根据黄金分割点的另一种表示：若线段长为$a$，则较短线段长为$(3 - \sqrt{5})\dfrac{a}{2}$（$a = 8$），$(3-\sqrt{5})×4=12 - 4\sqrt{5}\approx12-8.94=3.06$；
准确值为$12 - 4\sqrt{5}$，$12-4\sqrt{5}=4(3 - \sqrt{5})$，$\sqrt{5}\approx2.24$，$12-4\sqrt{5}=12-4×2.24 = 12 - 8.96 = 3.04$；
按照黄金分割公式：
设$PM=x$，$PQ = 8$，则$\dfrac{x}{8 - x}=\dfrac{8 - x}{8}$，$(8 - x)^{2}=8x$，$64-16x+x^{2}=8x$，$x^{2}-24x + 64 = 0$。
根据一元二次方程$ax^{2}+bx + c = 0(a = 1,b=-24,c = 64)$的求根公式$x=\dfrac{-b\pm\sqrt{b^{2}-4ac}}{2a}=\dfrac{24\pm\sqrt{576 - 256}}{2}=\dfrac{24\pm\sqrt{320}}{2}=\dfrac{24\pm8\sqrt{5}}{2}=12\pm4\sqrt{5}$。
因为$x\lt8$，所以$x = 12 - 4\sqrt{5}$。
所以她要站在最佳位置处时至少要走$(12 - 4\sqrt{5})$m。

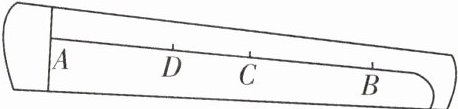
7. 如图,一种乐器上的一根弦AB= 80cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C,D之间的距离为$80\sqrt{5}-160$cm(结果保留根号).
]

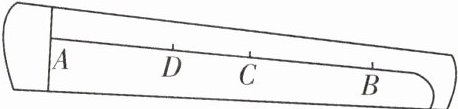
答案： $80\sqrt{5}-160$

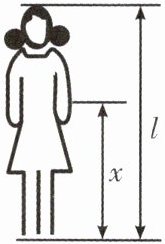
8. 美是一种感觉,当人体下半身长与身高的比值越接近0.618,越给人一种美感. 如图,一名模特的身高为165cm,下半身长x与身高l的比值是0.60,为尽可能展现服装的美,她穿的高跟鞋的高度应大约为多少厘米？
]

答案： 解：由题意得，模特下半身长 $ x = 165 × 0.60 = 99 \, cm $。
设高跟鞋高度为 $ h \, cm $，则此时下半身长为 $ (99 + h) \, cm $，身高为 $ (165 + h) \, cm $。
依题意，$ \frac{99 + h}{165 + h} = 0.618 $。
解得 $ h \approx 7.1 $。
答：她穿的高跟鞋的高度应大约为 $ 7.1 $ 厘米。