第137页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
1. 如图,某学校操场旗杆上高高飘扬着五星红旗,数学兴趣小组想测量旗杆的高度. 在离旗杆底部$a\ m$的$A$处,用高$1.5\ m$的测角仪$DA$测得旗杆顶端$C$的仰角为$\alpha$,则下列计算旗杆的高度$BC$正确的是 (
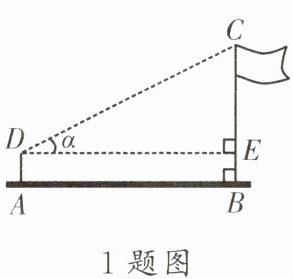
A.$(a\sin\alpha +1.5)\ m$
B.$(a\cos\alpha +1.5)\ m$
C.$(a\tan\alpha +1.5)\ m$
D.$\left(\frac{a}{\tan\alpha}+1.5\right)\ m$
C
)
A.$(a\sin\alpha +1.5)\ m$
B.$(a\cos\alpha +1.5)\ m$
C.$(a\tan\alpha +1.5)\ m$
D.$\left(\frac{a}{\tan\alpha}+1.5\right)\ m$
答案:
解:过点D作DE⊥BC于点E,
则四边形ABED为矩形,
∴DE=AB=a m,BE=AD=1.5 m,
在Rt△CDE中,∠CDE=α,
tanα=CE/DE,
∴CE=DE·tanα=a tanα m,
∴BC=CE+BE=a tanα +1.5 m,
故选C。
则四边形ABED为矩形,
∴DE=AB=a m,BE=AD=1.5 m,
在Rt△CDE中,∠CDE=α,
tanα=CE/DE,
∴CE=DE·tanα=a tanα m,
∴BC=CE+BE=a tanα +1.5 m,
故选C。
2. 如图,两建筑物水平距离$BD$为$32$米,从点$A$测得对面建筑物点$C$的俯角为$30°$,点$D$的俯角为$45°$,则建筑物$CD$的高约为 (

A.$14$米
B.$17$米
C.$20$米
D.$22$米
A
)
A.$14$米
B.$17$米
C.$20$米
D.$22$米
答案:
A
3. 如图,建筑物$BC$的屋顶有一根旗杆$AB$,小敏站在距离楼底端$C$点$25$米处的$D$点,测得此时旗杆顶点$A$的仰角为$50^\circ$,观测旗杆底部$B$点的仰角为$45^\circ$.(点$A$,$B$,$C$在同一直线上,且点$A$,$B$,$C$,$D$处于同一平面内,参考数据:$\sin50^\circ\approx0.8$,$\tan50^\circ\approx1.2$)
(1)求楼高$BC$.
(2)求旗杆的高度$AB$.
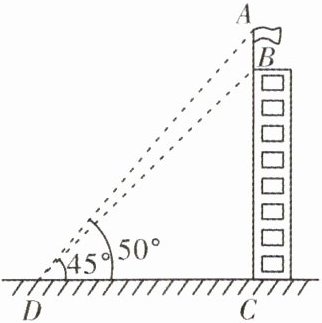
(1)求楼高$BC$.
(2)求旗杆的高度$AB$.

答案:
解:
(1)在Rt△BCD中,∠BDC=45°,CD=25米,∠BCD=90°,
∵tan∠BDC=BC/CD,
∴tan45°=BC/25,
∵tan45°=1,
∴BC=25×1=25米。
(2)在Rt△ACD中,∠ADC=50°,CD=25米,∠ACD=90°,
∵tan∠ADC=AC/CD,
∴tan50°=AC/25,
∵tan50°≈1.2,
∴AC≈25×1.2=30米,
∵AB=AC-BC,
∴AB≈30-25=5米。
答:
(1)楼高BC为25米;
(2)旗杆的高度AB约为5米。
(1)在Rt△BCD中,∠BDC=45°,CD=25米,∠BCD=90°,
∵tan∠BDC=BC/CD,
∴tan45°=BC/25,
∵tan45°=1,
∴BC=25×1=25米。
(2)在Rt△ACD中,∠ADC=50°,CD=25米,∠ACD=90°,
∵tan∠ADC=AC/CD,
∴tan50°=AC/25,
∵tan50°≈1.2,
∴AC≈25×1.2=30米,
∵AB=AC-BC,
∴AB≈30-25=5米。
答:
(1)楼高BC为25米;
(2)旗杆的高度AB约为5米。
4. 如图,河对岸有铁塔$AB$,$C$,$D$,$B$三点共线,在$C$处测得塔顶$A$的仰角为$30°$,向铁塔方向水平前进$14\ m$到达$D$,在$D$处测得$A$的仰角为$45°$,塔高$AB$为 (
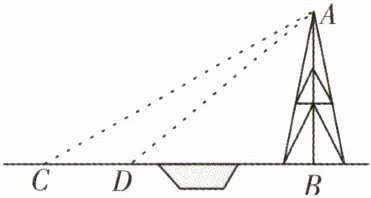
A.$4(4\sqrt{3}-1)\ m$
B.$7(\sqrt{3}+1)\ m$
C.$(16\sqrt{3}+7)\ m$
D.$(10\sqrt{3}+7)\ m$
B
)
A.$4(4\sqrt{3}-1)\ m$
B.$7(\sqrt{3}+1)\ m$
C.$(16\sqrt{3}+7)\ m$
D.$(10\sqrt{3}+7)\ m$
答案:
B
5. 如图1,望江楼是成都的代表性建筑,它依江而建,造型独特,气势磅礴,它不仅是观赏江景的好地方,还是文人墨客吟诗作画的场所,夜晚的望江楼更是绝美. 小风家楼顶恰好能看到望江楼及水中倒影,其示意图如图2所示,小风利用测角仪在$A$处测得望江楼顶$C$处的俯角$\angle FAC=31°$,望江楼顶在水中的倒影$E$处的俯角$\angle FAE=54°$. 若小风家楼高$AB=100\ m$,求望江楼的高度$CD$.(结果精确到$1\ m$. 参考数据:$\sin31°\approx0.52$,$\cos31°\approx0.86$,$\tan31°\approx0.60$,$\sin54°\approx0.81$,$\cos54°\approx0.59$,$\tan54°\approx1.38$)

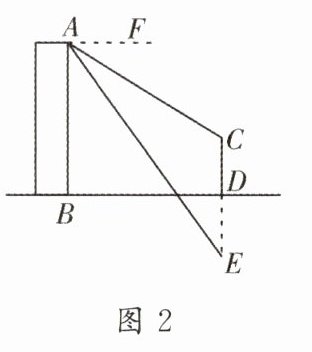


答案:
【解析】:本题主要考查了解直角三角形的应用,关键是构造仰角和俯角所在的直角三角形,利用两个直角三角形的公共边求解。
过点$A$作$AH\perp CD$于点$H$,则四边形$ABDH$是矩形,
所以$HD=AB=100\ m$,$\angle EAH=54°$,$\angle CAH=31°$,
设$CH=x\ m$,
在$Rt\triangle ACH$中,$\tan\angle CAH=\frac{CH}{AH}$,
所以$AH=\frac{CH}{\tan\angle CAH}=\frac{x}{\tan31°}$,
在$Rt\triangle AHE$中,$\tan\angle EAH=\frac{HE}{AH}$,
所以$HE=AH\tan\angle EAH=\frac{x}{\tan31°}\tan54°$,
又因为$HE-CH=HD=100\ m$,
所以可列出方程$\frac{x}{\tan31°}\tan54°-x=100$,
即$\frac{x}{0.60}×1.38-x=100$,
$\frac{1.38x}{0.60}-x=100$,
$\frac{23x}{10}×\frac{100}{60}-x=100$,
$\frac{23x}{6}-x=100$,
$\frac{23x-6x}{6}=100$,
$\frac{17x}{6}=100$,
$17x=600$,
解得$x=\frac{600}{17}\approx35.29$,
则$CD=CH+HD=35.29+100\approx135\ m$。
【答案】:望江楼的高度$CD$约为$135\ m$。
过点$A$作$AH\perp CD$于点$H$,则四边形$ABDH$是矩形,
所以$HD=AB=100\ m$,$\angle EAH=54°$,$\angle CAH=31°$,
设$CH=x\ m$,
在$Rt\triangle ACH$中,$\tan\angle CAH=\frac{CH}{AH}$,
所以$AH=\frac{CH}{\tan\angle CAH}=\frac{x}{\tan31°}$,
在$Rt\triangle AHE$中,$\tan\angle EAH=\frac{HE}{AH}$,
所以$HE=AH\tan\angle EAH=\frac{x}{\tan31°}\tan54°$,
又因为$HE-CH=HD=100\ m$,
所以可列出方程$\frac{x}{\tan31°}\tan54°-x=100$,
即$\frac{x}{0.60}×1.38-x=100$,
$\frac{1.38x}{0.60}-x=100$,
$\frac{23x}{10}×\frac{100}{60}-x=100$,
$\frac{23x}{6}-x=100$,
$\frac{23x-6x}{6}=100$,
$\frac{17x}{6}=100$,
$17x=600$,
解得$x=\frac{600}{17}\approx35.29$,
则$CD=CH+HD=35.29+100\approx135\ m$。
【答案】:望江楼的高度$CD$约为$135\ m$。
查看更多完整答案,请扫码查看


