第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
9. 如图,在□ABCD中,AD= 10 cm,CD= 6 cm,E为AD上一点,且BE= BC,CE= CD,则DE=

3.6
cm.

答案:
1. 首先,利用平行四边形的性质:
因为四边形$ABCD$是平行四边形,所以$AD// BC$,$AD = BC = 10cm$,$AB = CD = 6cm$。
由$AD// BC$可得$\angle DEC=\angle ECB$。
又因为$CE = CD = 6cm$,$BE = BC = 10cm$,所以$\angle D=\angle DEC$,$\angle BEC=\angle ECB$。
从而$\angle D=\angle DEC=\angle ECB=\angle BEC$。
2. 然后,证明$\triangle CDE\sim\triangle BEC$:
在$\triangle CDE$和$\triangle BEC$中,$\left\{\begin{array}{l}\angle D=\angle BEC\\\angle DEC=\angle ECB\end{array}\right.$,根据两角分别相等的两个三角形相似,所以$\triangle CDE\sim\triangle BEC$。
3. 接着,根据相似三角形的性质:
由相似三角形的性质可知$\frac{DE}{CE}=\frac{CE}{BC}$(相似三角形对应边成比例)。
已知$CE = 6cm$,$BC = 10cm$,设$DE=x cm$,则$\frac{x}{6}=\frac{6}{10}$。
所以$DE = 3.6cm$。
因为四边形$ABCD$是平行四边形,所以$AD// BC$,$AD = BC = 10cm$,$AB = CD = 6cm$。
由$AD// BC$可得$\angle DEC=\angle ECB$。
又因为$CE = CD = 6cm$,$BE = BC = 10cm$,所以$\angle D=\angle DEC$,$\angle BEC=\angle ECB$。
从而$\angle D=\angle DEC=\angle ECB=\angle BEC$。
2. 然后,证明$\triangle CDE\sim\triangle BEC$:
在$\triangle CDE$和$\triangle BEC$中,$\left\{\begin{array}{l}\angle D=\angle BEC\\\angle DEC=\angle ECB\end{array}\right.$,根据两角分别相等的两个三角形相似,所以$\triangle CDE\sim\triangle BEC$。
3. 接着,根据相似三角形的性质:
由相似三角形的性质可知$\frac{DE}{CE}=\frac{CE}{BC}$(相似三角形对应边成比例)。
已知$CE = 6cm$,$BC = 10cm$,设$DE=x cm$,则$\frac{x}{6}=\frac{6}{10}$。
所以$DE = 3.6cm$。
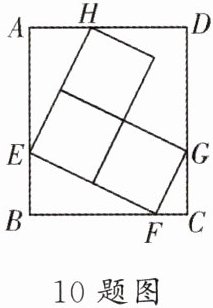
10. ▶中考热点·模型思想 如图,在长方形ABCD中,内接三个大小相同的正方形,点E,F,G,H分别在边AB,BC,CD,AD上,若AB= 12 cm,BC= 10 cm,则每个小正方形的边长为

4
cm.
答案:
解:设每个小正方形的边长为 $ x $ cm。
由题意,长方形 $ ABCD $ 中,$ AB=12 $ cm,$ BC=10 $ cm,内接三个大小相同的正方形,可得:
$ 2x + \frac{10 - x}{x} \cdot x = 12 $(或通过相似三角形对应边成比例:$\frac{10 - x}{x} = \frac{x}{12 - 2x}$)
解方程 $\frac{10 - x}{x} = \frac{x}{12 - 2x}$,
交叉相乘得:$ x^2 = (10 - x)(12 - 2x) $
展开得:$ x^2 = 120 - 20x - 12x + 2x^2 $
移项合并得:$ x^2 - 32x + 120 = 0 $
因式分解得:$(x - 30)(x - 4) = 0$
解得 $ x = 30 $(舍去)或 $ x = 4 $
4
由题意,长方形 $ ABCD $ 中,$ AB=12 $ cm,$ BC=10 $ cm,内接三个大小相同的正方形,可得:
$ 2x + \frac{10 - x}{x} \cdot x = 12 $(或通过相似三角形对应边成比例:$\frac{10 - x}{x} = \frac{x}{12 - 2x}$)
解方程 $\frac{10 - x}{x} = \frac{x}{12 - 2x}$,
交叉相乘得:$ x^2 = (10 - x)(12 - 2x) $
展开得:$ x^2 = 120 - 20x - 12x + 2x^2 $
移项合并得:$ x^2 - 32x + 120 = 0 $
因式分解得:$(x - 30)(x - 4) = 0$
解得 $ x = 30 $(舍去)或 $ x = 4 $
4
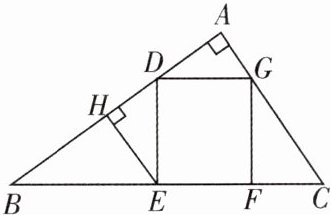
11. 如图,正方形DEFG内接于Rt△ABC,EF在斜边BC上,EH⊥AB于点H. 求证:
(1)△ADG≌△HED.
(2)$EF^2= BE\cdot FC$.
(1)△ADG≌△HED.
(2)$EF^2= BE\cdot FC$.

答案:
(1)证明:
∵四边形DEFG是正方形,
∴DG=DE,∠GDE=90°,
∴∠ADG+∠HDE=90°,
∵EH⊥AB,
∴∠DHE=90°,
∴∠HED+∠HDE=90°,
∴∠ADG=∠HED,
∵∠A=∠DHE=90°,
∴△ADG≌△HED(AAS)。
(2)证明:
∵四边形DEFG是正方形,
∴DE=EF=FG,∠DEF=∠EFG=90°,
∴∠B+∠BEH=90°,
∵∠A=90°,
∴∠B+∠C=90°,
∴∠BEH=∠C,
∵∠BHE=∠GFC=90°,
∴△BHE∽△GFC,
∴$\frac{BE}{FG}=\frac{EH}{FC}$,
∵EH=AD,由
(1)知△ADG≌△HED,
∴EH=AD,又DG=EF,
在△ADG中,∠A=90°,
∵DG//BC,
∴△ADG∽△ABC,
∴$\frac{AD}{AB}=\frac{DG}{BC}$,但此处仅需EH=DG=EF,
即EH=EF,FG=EF,
∴$\frac{BE}{EF}=\frac{EF}{FC}$,
∴$EF^2=BE\cdot FC$。
(1)证明:
∵四边形DEFG是正方形,
∴DG=DE,∠GDE=90°,
∴∠ADG+∠HDE=90°,
∵EH⊥AB,
∴∠DHE=90°,
∴∠HED+∠HDE=90°,
∴∠ADG=∠HED,
∵∠A=∠DHE=90°,
∴△ADG≌△HED(AAS)。
(2)证明:
∵四边形DEFG是正方形,
∴DE=EF=FG,∠DEF=∠EFG=90°,
∴∠B+∠BEH=90°,
∵∠A=90°,
∴∠B+∠C=90°,
∴∠BEH=∠C,
∵∠BHE=∠GFC=90°,
∴△BHE∽△GFC,
∴$\frac{BE}{FG}=\frac{EH}{FC}$,
∵EH=AD,由
(1)知△ADG≌△HED,
∴EH=AD,又DG=EF,
在△ADG中,∠A=90°,
∵DG//BC,
∴△ADG∽△ABC,
∴$\frac{AD}{AB}=\frac{DG}{BC}$,但此处仅需EH=DG=EF,
即EH=EF,FG=EF,
∴$\frac{BE}{EF}=\frac{EF}{FC}$,
∴$EF^2=BE\cdot FC$。
12. ▶中考热点·构造法【问题提出】
(1)如图1,在△ABC中,$\angle C= 90°$,点D在AC上,DE⊥AB于点E. 若AD= 3,AB= 5,CD= 1,则AE的长为
【问题解决】
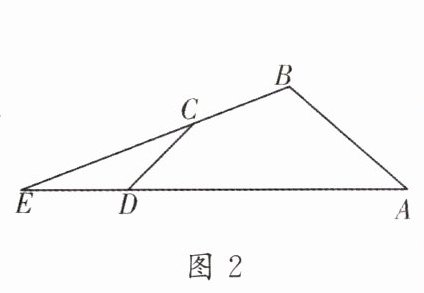
(2)如图2,有一块三角形试验田ECD,面积为14 m^2. 为了扩大试验规模,试验组决定将这个试验田扩建,考虑土壤、光照、温度、湿度、水源等诸多因素,最终扩建为三角形试验田ABE. 经实际测量可得$\angle ABC= 120°$,$\angle ADC= 45°$,CD= 4$\sqrt{2}$ m,AB= 10 m,求扩建后三角形试验田ABE的面积.

(1)如图1,在△ABC中,$\angle C= 90°$,点D在AC上,DE⊥AB于点E. 若AD= 3,AB= 5,CD= 1,则AE的长为
$\frac{9}{5}$
.【问题解决】
(2)如图2,有一块三角形试验田ECD,面积为14 m^2. 为了扩大试验规模,试验组决定将这个试验田扩建,考虑土壤、光照、温度、湿度、水源等诸多因素,最终扩建为三角形试验田ABE. 经实际测量可得$\angle ABC= 120°$,$\angle ADC= 45°$,CD= 4$\sqrt{2}$ m,AB= 10 m,求扩建后三角形试验田ABE的面积.


解:过点 $ C $ 作 $ CF \perp AD $ 于点 $ F $。
在 $ Rt\triangle CDF $ 中,$ \angle ADC = 45° $,$ CD = 4\sqrt{2} $,
$ CF = CD \cdot \sin 45° = 4\sqrt{2} × \frac{\sqrt{2}}{2} = 4 \, m $。
$ S_{\triangle ECD} = \frac{1}{2} \cdot ED \cdot CF = 14 $,即 $ \frac{1}{2} \cdot ED \cdot 4 = 14 $,解得 $ ED = 7 \, m $。
过点 $ B $ 作 $ BG \perp AD $ 交 $ AD $ 延长线于点 $ G $,设 $ BG = x $。
$ \angle ABC = 120° $,$ \angle BCG = 60° $,$ \angle CBG = 30° $,$ CG = \frac{BG}{\tan 60°} = \frac{x}{\sqrt{3}} $。
$ \angle ADC = 45° $,$ \angle A = \angle A $,$ \triangle AED \sim \triangle ABG $(AA相似)。
$ \frac{ED}{BG} = \frac{AD}{AG} $,$ AG = AD + DG = AD + (CG - CD \cdot \cos 45°) $,
$ CD \cdot \cos 45° = 4 $,$ CG = \frac{x}{\sqrt{3}} $,$ DG = \frac{x}{\sqrt{3}} - 4 $,$ AG = AD + \frac{x}{\sqrt{3}} - 4 $。
由 $ \frac{7}{x} = \frac{AD}{AD + \frac{x}{\sqrt{3}} - 4} $,解得 $ x = 5\sqrt{3} $。
$ S_{\triangle ABE} = \frac{1}{2} \cdot AB \cdot BG = \frac{1}{2} × 10 × 5\sqrt{3} = 25\sqrt{3} \, m^2 $。
答:扩建后三角形试验田 $ ABE $ 的面积为 $ 25\sqrt{3} \, m^2 $。
在 $ Rt\triangle CDF $ 中,$ \angle ADC = 45° $,$ CD = 4\sqrt{2} $,
$ CF = CD \cdot \sin 45° = 4\sqrt{2} × \frac{\sqrt{2}}{2} = 4 \, m $。
$ S_{\triangle ECD} = \frac{1}{2} \cdot ED \cdot CF = 14 $,即 $ \frac{1}{2} \cdot ED \cdot 4 = 14 $,解得 $ ED = 7 \, m $。
过点 $ B $ 作 $ BG \perp AD $ 交 $ AD $ 延长线于点 $ G $,设 $ BG = x $。
$ \angle ABC = 120° $,$ \angle BCG = 60° $,$ \angle CBG = 30° $,$ CG = \frac{BG}{\tan 60°} = \frac{x}{\sqrt{3}} $。
$ \angle ADC = 45° $,$ \angle A = \angle A $,$ \triangle AED \sim \triangle ABG $(AA相似)。
$ \frac{ED}{BG} = \frac{AD}{AG} $,$ AG = AD + DG = AD + (CG - CD \cdot \cos 45°) $,
$ CD \cdot \cos 45° = 4 $,$ CG = \frac{x}{\sqrt{3}} $,$ DG = \frac{x}{\sqrt{3}} - 4 $,$ AG = AD + \frac{x}{\sqrt{3}} - 4 $。
由 $ \frac{7}{x} = \frac{AD}{AD + \frac{x}{\sqrt{3}} - 4} $,解得 $ x = 5\sqrt{3} $。
$ S_{\triangle ABE} = \frac{1}{2} \cdot AB \cdot BG = \frac{1}{2} × 10 × 5\sqrt{3} = 25\sqrt{3} \, m^2 $。
答:扩建后三角形试验田 $ ABE $ 的面积为 $ 25\sqrt{3} \, m^2 $。
答案:
(1) $\frac{9}{5}$
(2) 解:过点 $ C $ 作 $ CF \perp AD $ 于点 $ F $。
在 $ Rt\triangle CDF $ 中,$ \angle ADC = 45^\circ $,$ CD = 4\sqrt{2} $,
$ CF = CD \cdot \sin 45^\circ = 4\sqrt{2} × \frac{\sqrt{2}}{2} = 4 \, m $。
$ S_{\triangle ECD} = \frac{1}{2} \cdot ED \cdot CF = 14 $,即 $ \frac{1}{2} \cdot ED \cdot 4 = 14 $,解得 $ ED = 7 \, m $。
过点 $ B $ 作 $ BG \perp AD $ 交 $ AD $ 延长线于点 $ G $,设 $ BG = x $。
$ \angle ABC = 120^\circ $,$ \angle BCG = 60^\circ $,$ \angle CBG = 30^\circ $,$ CG = \frac{BG}{\tan 60^\circ} = \frac{x}{\sqrt{3}} $。
$ \angle ADC = 45^\circ $,$ \angle A = \angle A $,$ \triangle AED \sim \triangle ABG $(AA相似)。
$ \frac{ED}{BG} = \frac{AD}{AG} $,$ AG = AD + DG = AD + (CG - CD \cdot \cos 45^\circ) $,
$ CD \cdot \cos 45^\circ = 4 $,$ CG = \frac{x}{\sqrt{3}} $,$ DG = \frac{x}{\sqrt{3}} - 4 $,$ AG = AD + \frac{x}{\sqrt{3}} - 4 $。
由 $ \frac{7}{x} = \frac{AD}{AD + \frac{x}{\sqrt{3}} - 4} $,解得 $ x = 5\sqrt{3} $。
$ S_{\triangle ABE} = \frac{1}{2} \cdot AB \cdot BG = \frac{1}{2} × 10 × 5\sqrt{3} = 25\sqrt{3} \, m^2 $。
答:扩建后三角形试验田 $ ABE $ 的面积为 $ 25\sqrt{3} \, m^2 $。
(注:实际计算中利用相似比直接求得 $ BG = 5\sqrt{3} $,最终面积为 $ 25\sqrt{3} $。)
答案:
(1) $\frac{9}{5}$;
(2) $25\sqrt{3} \, m^2$
(1) $\frac{9}{5}$
(2) 解:过点 $ C $ 作 $ CF \perp AD $ 于点 $ F $。
在 $ Rt\triangle CDF $ 中,$ \angle ADC = 45^\circ $,$ CD = 4\sqrt{2} $,
$ CF = CD \cdot \sin 45^\circ = 4\sqrt{2} × \frac{\sqrt{2}}{2} = 4 \, m $。
$ S_{\triangle ECD} = \frac{1}{2} \cdot ED \cdot CF = 14 $,即 $ \frac{1}{2} \cdot ED \cdot 4 = 14 $,解得 $ ED = 7 \, m $。
过点 $ B $ 作 $ BG \perp AD $ 交 $ AD $ 延长线于点 $ G $,设 $ BG = x $。
$ \angle ABC = 120^\circ $,$ \angle BCG = 60^\circ $,$ \angle CBG = 30^\circ $,$ CG = \frac{BG}{\tan 60^\circ} = \frac{x}{\sqrt{3}} $。
$ \angle ADC = 45^\circ $,$ \angle A = \angle A $,$ \triangle AED \sim \triangle ABG $(AA相似)。
$ \frac{ED}{BG} = \frac{AD}{AG} $,$ AG = AD + DG = AD + (CG - CD \cdot \cos 45^\circ) $,
$ CD \cdot \cos 45^\circ = 4 $,$ CG = \frac{x}{\sqrt{3}} $,$ DG = \frac{x}{\sqrt{3}} - 4 $,$ AG = AD + \frac{x}{\sqrt{3}} - 4 $。
由 $ \frac{7}{x} = \frac{AD}{AD + \frac{x}{\sqrt{3}} - 4} $,解得 $ x = 5\sqrt{3} $。
$ S_{\triangle ABE} = \frac{1}{2} \cdot AB \cdot BG = \frac{1}{2} × 10 × 5\sqrt{3} = 25\sqrt{3} \, m^2 $。
答:扩建后三角形试验田 $ ABE $ 的面积为 $ 25\sqrt{3} \, m^2 $。
(注:实际计算中利用相似比直接求得 $ BG = 5\sqrt{3} $,最终面积为 $ 25\sqrt{3} $。)
答案:
(1) $\frac{9}{5}$;
(2) $25\sqrt{3} \, m^2$
查看更多完整答案,请扫码查看


