第134页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
7. 如图,在Rt△ABC中,∠ACB= 90°,点D是AB的中点,连接CD,过点D作DE⊥CD,交BC于点E,若$tanA= \frac{4}{3},$BE= 7,则DE的长为
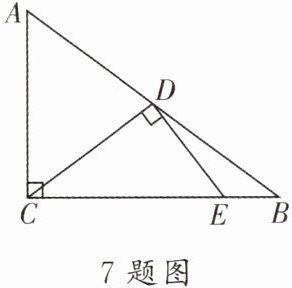
3
.
答案:
解:设AC=3k,BC=4k(k>0),则AB=5k。
∵D是AB中点,
∴CD=AD=BD=2.5k,∠A=∠ACD。
过D作DF⊥BC于F,DF=1.5k,CF=2k,设EF=x,则CE=2k-x,BE=4k-(2k-x)=2k+x=7。
∵∠CDE=90°,
∴△CDF∽△DEF,$\frac{CF}{DF}=\frac{DF}{EF}$,即$\frac{2k}{1.5k}=\frac{1.5k}{x}$,解得$x=\frac{9}{8}k$。
由2k+$\frac{9}{8}k$=7,得k=$\frac{8}{5}$,DE=$\sqrt{(1.5k)^2+x^2}$=3。
3
∵D是AB中点,
∴CD=AD=BD=2.5k,∠A=∠ACD。
过D作DF⊥BC于F,DF=1.5k,CF=2k,设EF=x,则CE=2k-x,BE=4k-(2k-x)=2k+x=7。
∵∠CDE=90°,
∴△CDF∽△DEF,$\frac{CF}{DF}=\frac{DF}{EF}$,即$\frac{2k}{1.5k}=\frac{1.5k}{x}$,解得$x=\frac{9}{8}k$。
由2k+$\frac{9}{8}k$=7,得k=$\frac{8}{5}$,DE=$\sqrt{(1.5k)^2+x^2}$=3。
3
8. 如图,在△ABC中,AB= BC,$tan∠B= \frac{5}{12},$D为BC上一点,若满足$CD= \frac{5}{8}BD,$过点D作DE⊥AD,交AC的延长线于点E,则\frac{CE}{AC}= ______
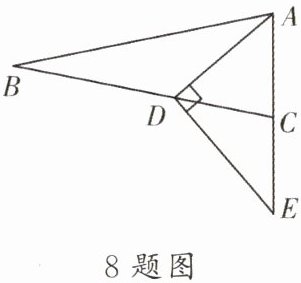
$\frac{5}{4}$
.
答案:
解:设 $ BD = 8k $,则 $ CD = \frac{5}{8}BD = 5k $,$ BC = BD + CD = 13k $。
∵ $ AB = BC $,
∴ $ AB = 13k $。
过点 $ A $ 作 $ AF \perp BC $ 于点 $ F $。
在 $ Rt\triangle ABF $ 中,$ \tan\angle B = \frac{AF}{BF} = \frac{5}{12} $,设 $ AF = 5m $,$ BF = 12m $。
由勾股定理得 $ AB^2 = AF^2 + BF^2 $,即 $ (13k)^2 = (5m)^2 + (12m)^2 $,解得 $ m = k $。
∴ $ AF = 5k $,$ BF = 12k $,$ FC = BC - BF = 13k - 12k = k $。
过点 $ C $ 作 $ CG \perp BC $ 交 $ DE $ 于点 $ G $。
∵ $ DE \perp AD $,$ CG \perp BC $,$ AF \perp BC $,
∴ $ \angle ADE = \angle DGC = \angle AFD = 90° $。
∵ $ \angle ADF + \angle EDG = 90° $,$ \angle EDG + \angle GDC = 90° $,
∴ $ \angle ADF = \angle GDC $。
∴ $ \triangle AFD \sim \triangle CGD $,$ \frac{AF}{CG} = \frac{FD}{CD} $。
$ FD = BF - BD = 12k - 8k = 4k $,$ CD = 5k $,$ AF = 5k $,$ \frac{5k}{CG} = \frac{4k}{5k} $,解得 $ CG = \frac{25k}{4} $。
∵ $ AF \perp BC $,$ CG \perp BC $,
∴ $ AF // CG $,$ \triangle AFC \sim \triangle EGC $,$ \frac{AF}{CG} = \frac{AC}{CE} $。
$ AC = \sqrt{AF^2 + FC^2} = \sqrt{(5k)^2 + k^2} = \sqrt{26}k $。
$ \frac{5k}{\frac{25k}{4}} = \frac{AC}{CE} $,$ \frac{4}{5} = \frac{AC}{CE} $,$ \frac{CE}{AC} = \frac{5}{4} $。
$\boxed{\frac{5}{4}}$
∵ $ AB = BC $,
∴ $ AB = 13k $。
过点 $ A $ 作 $ AF \perp BC $ 于点 $ F $。
在 $ Rt\triangle ABF $ 中,$ \tan\angle B = \frac{AF}{BF} = \frac{5}{12} $,设 $ AF = 5m $,$ BF = 12m $。
由勾股定理得 $ AB^2 = AF^2 + BF^2 $,即 $ (13k)^2 = (5m)^2 + (12m)^2 $,解得 $ m = k $。
∴ $ AF = 5k $,$ BF = 12k $,$ FC = BC - BF = 13k - 12k = k $。
过点 $ C $ 作 $ CG \perp BC $ 交 $ DE $ 于点 $ G $。
∵ $ DE \perp AD $,$ CG \perp BC $,$ AF \perp BC $,
∴ $ \angle ADE = \angle DGC = \angle AFD = 90° $。
∵ $ \angle ADF + \angle EDG = 90° $,$ \angle EDG + \angle GDC = 90° $,
∴ $ \angle ADF = \angle GDC $。
∴ $ \triangle AFD \sim \triangle CGD $,$ \frac{AF}{CG} = \frac{FD}{CD} $。
$ FD = BF - BD = 12k - 8k = 4k $,$ CD = 5k $,$ AF = 5k $,$ \frac{5k}{CG} = \frac{4k}{5k} $,解得 $ CG = \frac{25k}{4} $。
∵ $ AF \perp BC $,$ CG \perp BC $,
∴ $ AF // CG $,$ \triangle AFC \sim \triangle EGC $,$ \frac{AF}{CG} = \frac{AC}{CE} $。
$ AC = \sqrt{AF^2 + FC^2} = \sqrt{(5k)^2 + k^2} = \sqrt{26}k $。
$ \frac{5k}{\frac{25k}{4}} = \frac{AC}{CE} $,$ \frac{4}{5} = \frac{AC}{CE} $,$ \frac{CE}{AC} = \frac{5}{4} $。
$\boxed{\frac{5}{4}}$
9. 如图,在四边形ABCD中,∠ABC= 90°,∠C= 60°,$AB= \frac{\sqrt{3}}{2},$$BC= 1+\sqrt{3},$CD= 2.
(1)求tan∠ABD的值.
(2)求AD的长.
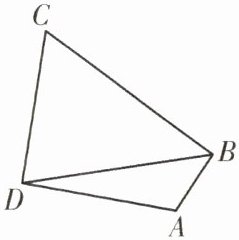
(1)求tan∠ABD的值.
(2)求AD的长.

答案:
解:
(1)过点D作DE⊥BC于点E,DF⊥AB交AB延长线于点F。
在Rt△CDE中,∠C=60°,CD=2,
CE=CD·cos60°=2×1/2=1,
DE=CD·sin60°=2×√3/2=√3。
BC=1+√3,BE=BC-CE=1+√3-1=√3。
∵∠ABC=90°,DE⊥BC,DF⊥AB,
∴四边形DEBF是矩形,BF=DE=√3,DF=BE=√3。
AB=√3/2,AF=AB+BF=√3/2+√3=3√3/2。
在Rt△ADF中,tan∠ABD=DF/AF=√3/(3√3/2)=2/3。
(2)在Rt△ADF中,AD=√(AF²+DF²)=√[(3√3/2)²+(√3)²]=√(27/4+3)=√(39/4)=√39/2。
(1)2/3;
(2)√39/2。
(1)过点D作DE⊥BC于点E,DF⊥AB交AB延长线于点F。
在Rt△CDE中,∠C=60°,CD=2,
CE=CD·cos60°=2×1/2=1,
DE=CD·sin60°=2×√3/2=√3。
BC=1+√3,BE=BC-CE=1+√3-1=√3。
∵∠ABC=90°,DE⊥BC,DF⊥AB,
∴四边形DEBF是矩形,BF=DE=√3,DF=BE=√3。
AB=√3/2,AF=AB+BF=√3/2+√3=3√3/2。
在Rt△ADF中,tan∠ABD=DF/AF=√3/(3√3/2)=2/3。
(2)在Rt△ADF中,AD=√(AF²+DF²)=√[(3√3/2)²+(√3)²]=√(27/4+3)=√(39/4)=√39/2。
(1)2/3;
(2)√39/2。
10. 中考热点·应用意识 阅读下列材料并解决问题.
如图1,在△ABC中,∠BAC,∠B,∠C所对的边分别为a,b,c,求证:$S_{\triangle ABC}= \frac{1}{2}absinC= \frac{1}{2}acsinB= \frac{1}{2}bcsinA.$证明:过点A作AD⊥BC,垂足为D,
在Rt△ABD中,$sinB= \frac{AD}{c},$
∴AD= c·sinB,
∴$S_{\triangle ABC}= \frac{1}{2}a·AD= \frac{1}{2}acsinB.$同理,$S_{\triangle ABC}= \frac{1}{2}absinC,$$S_{\triangle ABC}= \frac{1}{2}bcsinA,$
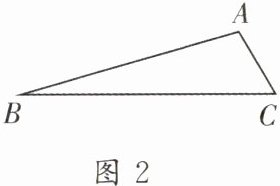
∴$S_{\triangle ABC}= \frac{1}{2}absinC= \frac{1}{2}acsinB= \frac{1}{2}bcsinA.(1)$求证:$\frac{a}{sinA}= \frac{b}{sinB}= \frac{c}{sinC}.(2)$运用(1)中的结论解决问题:如图2,在△ABC中,∠B= 15°,∠C= 60°,$AB= 20\sqrt{3},$则AC的长度为
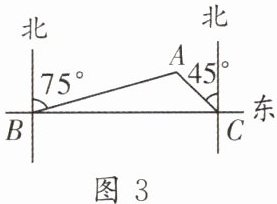
(3)如图3,为了开发三角形荒地ABC,测量人员在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18 km到达C点,测得A在北偏西45°方向上.根据以上信息,求三角形荒地的面积.(参考数值:sin15°≈0.3,sin120°≈0.9,$\sqrt{2}≈1.4,$结果取整数)
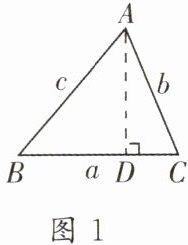
如图1,在△ABC中,∠BAC,∠B,∠C所对的边分别为a,b,c,求证:$S_{\triangle ABC}= \frac{1}{2}absinC= \frac{1}{2}acsinB= \frac{1}{2}bcsinA.$证明:过点A作AD⊥BC,垂足为D,
在Rt△ABD中,$sinB= \frac{AD}{c},$
∴AD= c·sinB,
∴$S_{\triangle ABC}= \frac{1}{2}a·AD= \frac{1}{2}acsinB.$同理,$S_{\triangle ABC}= \frac{1}{2}absinC,$$S_{\triangle ABC}= \frac{1}{2}bcsinA,$
∴$S_{\triangle ABC}= \frac{1}{2}absinC= \frac{1}{2}acsinB= \frac{1}{2}bcsinA.(1)$求证:$\frac{a}{sinA}= \frac{b}{sinB}= \frac{c}{sinC}.(2)$运用(1)中的结论解决问题:如图2,在△ABC中,∠B= 15°,∠C= 60°,$AB= 20\sqrt{3},$则AC的长度为
12
.(3)如图3,为了开发三角形荒地ABC,测量人员在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18 km到达C点,测得A在北偏西45°方向上.根据以上信息,求三角形荒地的面积.(参考数值:sin15°≈0.3,sin120°≈0.9,$\sqrt{2}≈1.4,$结果取整数)



38
答案:
(2)$12$;
(3)$38$。
(2)$12$;
(3)$38$。
查看更多完整答案,请扫码查看


