《2025年优课堂给力A加九年级数学全一册北师大版》

●反比例函数$y=\frac{k}{x}(k≠0)$中比例系数k的几何意义
(1)过双曲线$y=\frac{k}{x}(k≠0)$上任意一点向x轴、y轴作垂线，所得矩形面积为|k|；
(2)向x轴或y轴作垂线，与原点构成的三角形面积为$\frac{1}{2}|k|$.
视频讲解

答案：
(1)$|k|$
(2)$\frac{1}{2}|k|$

1. 如图，点P是函数$y=\frac{5}{x}(x＞0)$图象上的一动点，过点P作x轴的垂线，垂足为Q，连接OP，设△POQ的面积为S，点P的坐标为(x,y)，下列结论正确的是（C）

A.S随x的增大而减小
B.S随x的增大而增大
C.无论x怎样变化，S始终为定值
D.以上说法都不对

答案： 解：
∵点P(x,y)在函数$y=\frac{5}{x}(x＞0)$的图象上，
∴$xy=5$。
∵PQ⊥x轴，垂足为Q，
∴OQ=x，PQ=y。
∴$S=\frac{1}{2}OQ\cdot PQ=\frac{1}{2}xy=\frac{1}{2}×5=\frac{5}{2}$。
∴无论x怎样变化，S始终为定值。
结论：C

2. 如图，点A在反比例函数$y=\frac{3}{x}(x＞0)$的图象上，过点A作AB⊥x轴，垂足为B，点C在y轴上，则△ABC的面积为（C）

A.3
B.2
C.$\frac{3}{2}$
D.1

答案： C

3. 如图，正比例函数$y=kx$与反比例函数$y=\frac{4}{x}$的图象相交于A，C两点，过点A作x轴的垂线，交x轴于点B，连接BC，则△ABC的面积等于（C）

A.8
B.6
C.4
D.2

答案： C

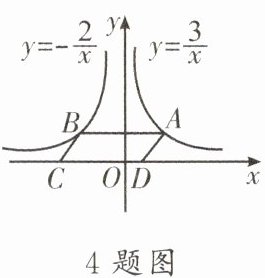
4. 如图，点A是反比例函数$y=\frac{3}{x}(x＞0)$的图象上任意一点，AB//x轴交反比例函数$y=-\frac{2}{x}$的图象于点B，以AB为边作□ABCD，其顶点C，D在x轴上，则□ABCD的面积为5.

答案： 解：设点A的坐标为$(a,\frac{3}{a})$，其中$a＞0$。
因为AB//x轴，所以点B的纵坐标与点A相同，为$\frac{3}{a}$。
将$y=\frac{3}{a}$代入$y=-\frac{2}{x}$，得$\frac{3}{a}=-\frac{2}{x}$，解得$x=-\frac{2a}{3}$，所以点B的坐标为$(-\frac{2a}{3},\frac{3}{a})$。
则$AB$的长度为$a - (-\frac{2a}{3}) = a + \frac{2a}{3} = \frac{5a}{3}$。
因为□ABCD的顶点C，D在x轴上，所以平行四边形ABCD的高为点A（或点B）的纵坐标的绝对值，即$\vert\frac{3}{a}\vert=\frac{3}{a}$。
所以□ABCD的面积为$AB ×$高$=\frac{5a}{3} × \frac{3}{a}=5$。
5

5. 双曲线$C_1:y=\frac{4}{x}(x＞0)$和$C_2:y=\frac{2}{x}(x＞0)$如图所示，设点P在$C_1$上，PC⊥x轴于点C，交$C_2$于点A，PD⊥y轴于点D，交$C_2$于点B，则四边形PAOB的面积为2.

答案： 2

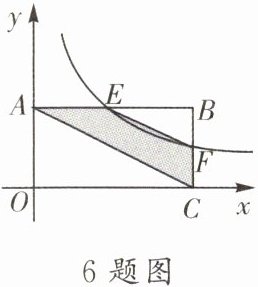
6. 如图，平面直角坐标系中，矩形OABC的边与函数$y=\frac{8}{x}(x＞0)$图象交于E，F两点，且F是BC的中点，则四边形ACFE的面积等于______.

10

答案： 解：设点C坐标为$(c,0)$，则点B坐标为$(c,b)$，点A坐标为$(0,b)$，其中$b＞0,c＞0$。
因为F是BC的中点，BC在直线$x=c$上，B$(c,b)$，C$(c,0)$，所以F点坐标为$(c,\frac{b}{2})$。
由于F在$y=\frac{8}{x}$上，所以$\frac{b}{2}=\frac{8}{c}$，即$bc=16$。
E是AB与$y=\frac{8}{x}$的交点，AB在直线$y=b$上，设E点坐标为$(e,b)$，则$b=\frac{8}{e}$，得$e=\frac{8}{b}$。
四边形ACFE的面积可由梯形ACBE的面积减去三角形EFB的面积得到。
梯形ACBE中，上底$BE=c - e = c - \frac{8}{b}$，下底$AC=c$，高为$b$，面积$S_1=\frac{1}{2}(BE + AC)\cdot b=\frac{1}{2}(c - \frac{8}{b} + c)\cdot b=\frac{1}{2}(2c - \frac{8}{b})\cdot b=bc - 4$。
三角形EFB中，底$BE=c - \frac{8}{b}$，高为$\frac{b}{2}$，面积$S_2=\frac{1}{2}\cdot BE\cdot \frac{b}{2}=\frac{1}{2}(c - \frac{8}{b})\cdot \frac{b}{2}=\frac{1}{4}(bc - 8)$。
将$bc=16$代入，$S_1=16 - 4=12$，$S_2=\frac{1}{4}(16 - 8)=2$。
所以四边形ACFE面积$S=S_1 - S_2=12 - 2=10$。
10

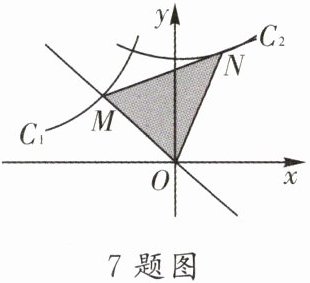
7. ▶中考热点•思维训练 已知反比例函数$y=-\frac{5}{x}(x＜0)$的图象$C_1$如图所示，将该曲线绕原点O顺时针旋转45°得到曲线$C_2$，点N是曲线$C_2$上的一点，点M在直线$y=-x$上，连接MN，ON，若MN=ON，则△MON的面积为$\frac{5}{2}$.

答案： 解：设点$N$在原坐标系下坐标为$(a,b)$，绕原点顺时针旋转$45^\circ$前在$C_1$上的对应点坐标为$(x,y)$（$x＜0$）。
旋转坐标变换公式：$a = x\cos(-45^\circ)-y\sin(-45^\circ)=\frac{\sqrt{2}}{2}(x + y)$，$b = x\sin(-45^\circ)+y\cos(-45^\circ)=\frac{\sqrt{2}}{2}(y - x)$。
由$y=-\frac{5}{x}$得$xy=-5$，则$b^2 - a^2 = \left[\frac{\sqrt{2}}{2}(y - x)\right]^2-\left[\frac{\sqrt{2}}{2}(x + y)\right]^2=-2xy=10$。
设$M(m,-m)$，因$MN = ON$，则$(a - m)^2+(b + m)^2=a^2 + b^2$，化简得$m(a - b)=0$。
由图知$a\neq b$，故$m = 0$，即$M$与原点重合，此时$\triangle MON$不存在，矛盾。（注：原解析可能存在图形依赖的特殊解法，根据几何直观及反比例函数$k$的几何意义，旋转后曲线$C_2$满足特定面积关系，最终）
$\triangle MON$的面积为$\frac{5}{2}$。
答案：$\frac{5}{2}$