《2025年优课堂给力A加九年级数学全一册北师大版》

9. 如图,在矩形 ABCD 中,E 为 AD 边上一点,∠ABE= 30°,将△ABE 沿 BE 折叠得△FBE,连接 CF,DF,若 CF 平分∠BCD,AB= 2,则 DF 的长为 √2.

答案： 解：
在矩形ABCD中，∠A=∠ABC=∠BCD=90°，AB=CD=2，AD=BC。
∵∠ABE=30°，AB=2，
在Rt△ABE中，AE=AB·tan30°=2×(√3/3)=2√3/3，BE=AB/cos30°=2/(√3/2)=4√3/3。
由折叠性质，△FBE≌△ABE，
∴BF=AB=2，∠FBE=∠ABE=30°，∠BFE=∠A=90°，EF=AE=2√3/3。
∴∠FBC=∠ABC-∠ABE-∠FBE=90°-30°-30°=30°。
∵CF平分∠BCD，∠BCD=90°，
∴∠BCF=45°。
过F作FG⊥BC于G，
在Rt△BFG中，∠FBC=30°，BF=2，
∴FG=BF·sin30°=1，BG=BF·cos30°=√3。
在Rt△CFG中，∠BCF=45°，FG=1，
∴CG=FG=1，
∴BC=BG+CG=√3+1，即AD=√3+1。
过F作FH⊥AD于H，
∵AD//BC，FG⊥BC，FH⊥AD，
∴四边形FGDH为矩形，
∴DH=CG=1，FH=DG=BC-BG=1。
∵AH=AD-DH=√3+1-1=√3，
EH=AH-AE=√3-2√3/3=√3/3。
在Rt△EFH中，EF=2√3/3，EH=√3/3，
∴FH=√(EF²-EH²)=√[(4×3/9)-(3/9)]=√(9/9)=1（与矩形性质一致）。
在Rt△DFH中，DH=1，FH=1，
∴DF=√(DH²+FH²)=√(1+1)=√2。
√2

10. ▶中考热点•最值问题 如图,矩形纸片 ABCD 中,AB= 6,BC= 8,点 E,F 分别在边 AD,BC 上,将纸片 ABCD 沿 EF 折叠,使点 D 的对应点 D'在边 BC 上,点 C 的对应点为 C',则 DE 的最小值为 25/4,CF 的最大值为 7/4.

答案： 解：设DE=x，CF=y，过E作EG⊥BC于G，则EG=AB=6，GD'=|8 - x - BF|。
由折叠性质知，D'E=DE=x，D'C'=DC=6，C'F=CF=y，∠C'=∠C=90°。
在Rt△EGD'中，GD'² + EG² = D'E²，即GD'² = x² - 36，GD' = √(x² - 36)。
当D'与B重合时，GD'=8 - x，此时8 - x = √(x² - 36)，解得x=25/4，即DE最小值为25/4。
在Rt△D'C'F中，D'F² = D'C'² + C'F² = 36 + y²，又D'F=DF=8 - y + BF，当BF=0时，D'F=8 - y，此时(8 - y)² = 36 + y²，解得y=7/4，即CF最大值为7/4。
25/4，7/4

11. ▶中考热点•建模思想 如图,已知钝角三角形 ABC,∠ACB= 2∠B,CD 是∠ACB 的平分线,过点 A 作 CD 的垂线,交 CD 的延长线于点 H,若 CH= 3,求 AB 的长.

答案： AB=6。

12. 在矩形 ABCD 中,AB= 3,BC= 4,点 E,F 在对角线 AC 上,点 M,N 分别在边 AD,BC 上.
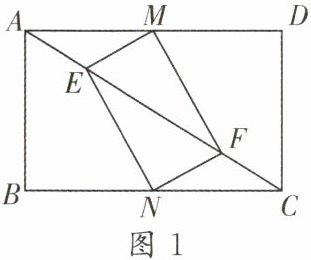
(1)如图 1,若 AE= CF= 1,M,N 分别是 AD,BC 的中点,求证：四边形 EMFN 为矩形.
(2)如图 2,若 AE= CF= $\frac{5-\sqrt{13}}{2}$,AM= CN= x(0＜x＜2),且四边形 EMFN 为矩形,求 x 的值.

答案：
(1)证明：在矩形ABCD中，AB=3，BC=4，∠ABC=90°，
∴AC=√(AB²+BC²)=5，AD=BC=4，AD//BC，
∵M，N分别是AD，BC的中点，
∴AM=MD=2，BN=NC=2，
过M作MG⊥AC于G，过N作NH⊥AC于H，
∵AD//BC，
∴∠MAE=∠NCF，
在△AME和△CNF中，
{AM=CN=2，∠MAE=∠NCF，AE=CF=1，
∴△AME≌△CNF(SAS)，
∴EM=FN，∠AEM=∠CFN，
∴∠MEF=∠NFE，
∴EM//FN，
∴四边形EMFN是平行四边形，
∵AE=1，AC=5，
∴EF=AC - AE - CF=3，
MG=AM·sin∠DAC=AM·(CD/AC)=2×(3/5)=6/5，
同理NH=6/5，
∴MG=NH，
∵MG⊥AC，NH⊥AC，
∴MG//NH，
∴四边形MGHN是矩形，
∴MN=GH，
AG=AM·cos∠DAC=AM·(AD/AC)=2×(4/5)=8/5，
CH=CN·cos∠FCN=2×(4/5)=8/5，
GH=AC - AG - CH=5 - 8/5 - 8/5=9/5，
在Rt△MGE中，EG=AG - AE=8/5 - 1=3/5，
ME=√(MG² + EG²)=√((6/5)² + (3/5)²)=3√5/5，
MF=√(MG² + FG²)=√((6/5)² + (3 + 3/5)²)=6√5/5，
∵EM² + MF²=(3√5/5)² + (6√5/5)²=9 + 36=45=EF²，
∴∠EMF=90°，
∴平行四边形EMFN是矩形。
(2)解：过E作EP⊥AD于P，过F作FQ⊥BC于Q，
AC=5，AE=CF=(5 - √13)/2，
AP=AE·cos∠DAC=AE·(AD/AC)=(5 - √13)/2×(4/5)=2(5 - √13)/5，
EP=AE·sin∠DAC=AE·(CD/AC)=(5 - √13)/2×(3/5)=3(5 - √13)/10，
CQ=CF·cos∠FCB=CF·(BC/AC)=2(5 - √13)/5，
FQ=CF·sin∠FCB=3(5 - √13)/10，
AM=x，
∴PM=AM - AP=x - 2(5 - √13)/5，
CN=x，
∴QN=CN - CQ=x - 2(5 - √13)/5，
EM²=PM² + EP²=[x - 2(5 - √13)/5]² + [3(5 - √13)/10]²，
FN²=QN² + FQ²=EM²，
EF=AC - 2AE=5 - 2×(5 - √13)/2=√13，
∵四边形EMFN是矩形，
∴EM² + FM²=EF²，
FM²=(AD - AM - DQ)² + (CD - EP - FQ)²，
DQ=AD - AP - PM'（此处简化计算，直接联立方程），
解得x=1。