第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
1. 小星同学通过大量重复的定点投篮练习,用频率估计他投中的概率为0.4,下列说法正确的是(
A.小星定点投篮1次,不一定能投中
B.小星定点投篮1次,一定可以投中
C.小星定点投篮10次,一定投中4次
D.小星定点投篮4次,一定投中1次
A
)A.小星定点投篮1次,不一定能投中
B.小星定点投篮1次,一定可以投中
C.小星定点投篮10次,一定投中4次
D.小星定点投篮4次,一定投中1次
答案:
A
2. 在一个不透明的袋子里装有除颜色外完全相同的若干个黑球和白球,小红摸出一个小球记录颜色后放回口袋,经过大量的摸球试验后发现摸到白球的频率稳定在0.2左右,那么摸出黑球的概率约为(
A.4/5
B.3/5
C.2/5
D.1/5
A
)A.4/5
B.3/5
C.2/5
D.1/5
答案:
A
3. 某林业部门要考察某种幼苗的成活率,于是进行了试验,下表中记录了这种幼苗在一定条件下移植的成活情况,则下列说法不正确的是(
| 移植总数n | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
| --- | --- | --- | --- | --- | --- | --- |
| 成活数m | 369 | 1335 | 3203 | 6335 | 8073 | 12628 |
| 成活的频率m/n | 0.923 | 0.890 | 0.915 | 0.905 | 0.897 | 0.902 |
A.由此估计这种幼苗在此条件下成活的概率约为0.9
B.如果在此条件下再移植这种幼苗20000株,则必定成活18000株
C.可以用试验次数累计最多时的频率作为概率的估计值
D.在大量重复试验中,随着试验次数的增加,幼苗成活的频率会越来越稳定,因此可以用频率估计概率
B
)| 移植总数n | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
| --- | --- | --- | --- | --- | --- | --- |
| 成活数m | 369 | 1335 | 3203 | 6335 | 8073 | 12628 |
| 成活的频率m/n | 0.923 | 0.890 | 0.915 | 0.905 | 0.897 | 0.902 |
A.由此估计这种幼苗在此条件下成活的概率约为0.9
B.如果在此条件下再移植这种幼苗20000株,则必定成活18000株
C.可以用试验次数累计最多时的频率作为概率的估计值
D.在大量重复试验中,随着试验次数的增加,幼苗成活的频率会越来越稳定,因此可以用频率估计概率
答案:
B
4. 在利用正六面体骰子进行用频率估计概率的试验中,小颖同学统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是(
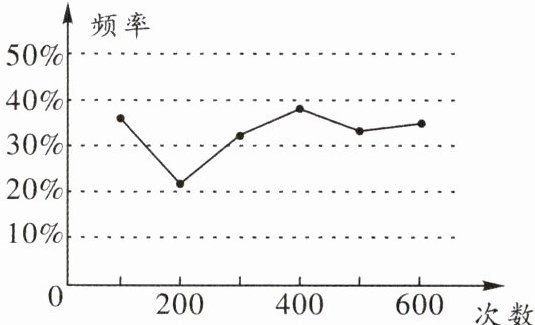
A.朝上的点数是5的概率
B.朝上的点数是奇数的概率
C.朝上的点数是大于2的概率
D.朝上的点数是3的倍数的概率
D
)
A.朝上的点数是5的概率
B.朝上的点数是奇数的概率
C.朝上的点数是大于2的概率
D.朝上的点数是3的倍数的概率
答案:
D
5. 为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生的身高x(cm)统计如下:
| 组别 | x<160 | 160≤x<170 | 170≤x<180 | x≥180 |
| --- | --- | --- | --- | --- |
| 人数 | 5 | 38 | 42 | 15 |
随机抽查该地区一名九年级男生,估计他的身高不低于180 cm的概率是(
A.0.85
B.0.57
C.0.42
D.0.15
| 组别 | x<160 | 160≤x<170 | 170≤x<180 | x≥180 |
| --- | --- | --- | --- | --- |
| 人数 | 5 | 38 | 42 | 15 |
随机抽查该地区一名九年级男生,估计他的身高不低于180 cm的概率是(
D
)A.0.85
B.0.57
C.0.42
D.0.15
答案:
D
6. 在一个不透明的口袋中装有红球和白球共12个,这些球除颜色外都相同,将口袋中的球搅匀后,从中随机摸出1个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸球200次,发现有50次摸到红球,则口袋中红球约有
3
个.
答案:
解:设口袋中红球约有$x$个。
由题意,摸到红球的频率为$\frac{50}{200} = 0.25$。
因为用频率估计概率,所以摸到红球的概率约为$0.25$。
又因为口袋中共有12个球,所以$\frac{x}{12} = 0.25$,解得$x = 3$。
答:口袋中红球约有$3$个。
由题意,摸到红球的频率为$\frac{50}{200} = 0.25$。
因为用频率估计概率,所以摸到红球的概率约为$0.25$。
又因为口袋中共有12个球,所以$\frac{x}{12} = 0.25$,解得$x = 3$。
答:口袋中红球约有$3$个。
7. 不透明的口袋里有除颜色外其他均相同的红、白、黑小球共计120个,玲玲通过多次摸球试验后发现,摸到红球和黑球的频率稳定在50%和30%,那么口袋中白球的个数极有可能是
24
个.
答案:
24
8. 一个口袋中放有红、蓝、黄三种颜色的小球若干个,这些小球除颜色不同外其余均相同. 小明进行了大量的摸球试验:随机摸出一球,记下颜色放回去,搅拌均匀再摸出一球,记下颜色再放回去……试验结束后,小明根据记录绘制了如图所示的尚不完整的条形统计图,并统计出:摸出黄球的次数是200,摸出红球的次数比摸出蓝球次数的2倍少100,摸出黄球的频率为0.2.
(1)小明共摸了多少次球?
(2)补全条形统计图.
(3)若口袋中共有12个小球,请用小明的试验结论估计其中红球的个数.
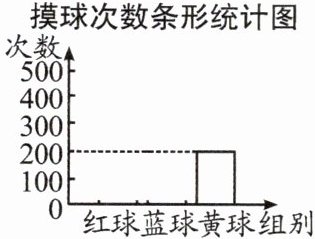
(1)小明共摸了多少次球?
(2)补全条形统计图.
(3)若口袋中共有12个小球,请用小明的试验结论估计其中红球的个数.

答案:
(1)1000;(2)红球次数为500,蓝球次数为300;(3)6。
查看更多完整答案,请扫码查看


