《2025年优课堂给力A加九年级数学全一册北师大版》

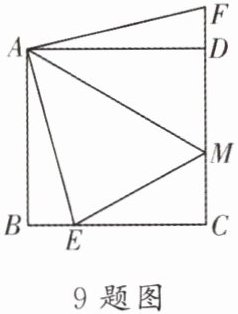
9. 如图,在边长为4的正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,AM平分∠EAF交CD于点M.若BE= DF= 1,则DM的长度为2.4.

答案： 2.4

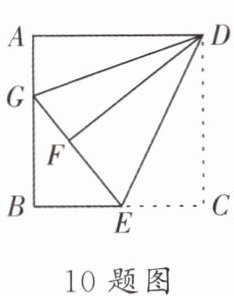
10. 如图,已知正方形ABCD的边长为12,BE= EC,将正方形的边CD沿DE折叠到DF,延长EF,交AB于点G,连接DG.现有如下3个结论：①AG+EC= GE；②∠GDE= 45°；③△BGE的周长是24.其中正确的有①②③.(选填序号)

答案： 解：①②③
证明：
∵正方形ABCD边长为12，BE=EC，
∴EC=BE=6，AD=DC=BC=AB=12，∠A=∠B=∠C=∠ADC=90°。
由折叠性质得：DF=DC=12，∠DFE=∠C=90°，EF=EC=6，∠FDE=∠CDE。
∵AD=DF=12，DG=DG，∠A=∠DFG=90°，
∴Rt△ADG≌Rt△FDG（HL），
∴AG=FG，∠ADG=∠FDG。
设AG=FG=x，则BG=12-x，GE=GF+EF=x+6。
在Rt△BGE中，BG²+BE²=GE²，即(12-x)²+6²=(x+6)²，
解得x=4，
∴AG=4，GE=4+6=10，
∵AG+EC=4+6=10=GE，
∴①正确。
∵∠GDE=∠FDG+∠FDE=1/2∠ADC=45°，
∴②正确。
△BGE周长=BG+BE+GE=(12-4)+6+10=24，
∴③正确。
综上，正确的有①②③。

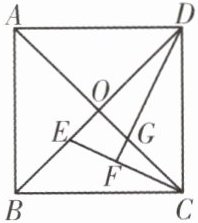
11. 如图,在正方形ABCD中,对角线AC,BD相交于点O,过点D作∠ODC的角平分线,交OC于点G,过点C作CF⊥DG,垂足为F,延长CF,交BD于点E.
(1)求证：OE= OG.
(2)求S△ADG:S△BCE的比值.

答案：
(1)证明：
∵四边形ABCD是正方形，
∴AC⊥BD，OD=OC，∠ODC=45°，∠DOC=∠COE=90°．
∵DG平分∠ODC，
∴∠ODG=∠CDG=22.5°．
∵CF⊥DG，
∴∠CFD=90°，
∴∠DCF+∠CDG=90°．
∵∠ODG+∠OGD=90°，∠ODG=∠CDG，
∴∠OGD=∠DCF．
在△ODG和△OCE中，
∠DOG=∠COE=90°，OD=OC，∠OGD=∠OCE，
∴△ODG≌△OCE(ASA)，
∴OE=OG．
(2)解：
设正方形边长为a，则AC=BD=√2a，OD=OC=√2a/2．
设OE=OG=x，则OG=x，CG=OC-OG=√2a/2 - x，OE=x，BE=OB+OE=√2a/2 + x．
∵DG平分∠ODC，
∴OG/CG=OD/CD（角平分线定理），
即x/(√2a/2 - x)=(√2a/2)/a，
解得x=(2-√2)a/2．
∴OG=(2-√2)a/2，CG=√2a/2 - (2-√2)a/2=(√2 -1)a．
S△ADG=S△ADC - S△CDG= (a²/2) - (1/2·CD·CG·sin45°)= (a²/2) - (1/2·a·(√2 -1)a·√2/2)= (2-√2)a²/4．
S△BCE= (1/2·BE·OC·sin45°)= (1/2·(√2a/2 + (2-√2)a/2)·√2a/2·√2/2)= (2+√2)a²/4．
∴S△ADG:S△BCE=(2-√2)/4 : (2+√2)/4= (2-√2)²/[(2+√2)(2-√2)]= (6-4√2)/2=3-2√2．
比值为3-2√2．

12. 中考热点•探索规律 如图,在正方形ABCD中,∠MAN= 45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM= DN时(如图1),求证：BM+DN= MN.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),则线段BM,DN和MN之间的数量关系是BM+DN=MN.
(3)当∠MAN绕点A旋转到如图3的位置时,猜想线段BM,DN和MN之间又有怎样的数量关系呢？请说明理由.

答案：
(1)证明：
∵四边形ABCD是正方形，
∴AB=AD，∠B=∠D=∠BAD=90°．
∵BM=DN，
∴△ABM≌△ADN(SAS)，
∴AM=AN，∠BAM=∠DAN．
∵∠MAN=45°，
∴∠BAM+∠DAN=∠BAD-∠MAN=45°，
∴∠BAM=∠DAN=22.5°．
延长CB至点E，使BE=DN，连接AE，
则△ABE≌△ADN(SAS)，
∴AE=AN，∠BAE=∠DAN=22.5°，
∴∠EAM=∠BAM+∠BAE=45°=∠MAN．
∵AM=AM，
∴△EAM≌△NAM(SAS)，
∴EM=MN．
∵EM=BE+BM=DN+BM，
∴BM+DN=MN．
(2)BM+DN=MN
(3)解：DN-BM=MN．
理由：在DN上截取DE=BM，连接AE．
∵四边形ABCD是正方形，
∴AB=AD，∠ABM=∠D=90°．
∵BM=DE，
∴△ABM≌△ADE(SAS)，
∴AM=AE，∠BAM=∠DAE．
∵∠MAN=45°，
∴∠MAE=∠BAD=90°，∠EAN=∠MAE-∠MAN=45°=∠MAN．
∵AN=AN，
∴△MAN≌△EAN(SAS)，
∴MN=EN．
∵EN=DN-DE=DN-BM，
∴DN-BM=MN．