第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
1. ▶中考热点•数学文化《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈(一丈= 十尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,求折断处离地面的高度. 设竹子折断处离地面x尺,根据题意,可列方程为(
A.${x}^{2}+{6}^{2}= {10}^{2}$
B.${(10-x)}^{2}+{6}^{2}= {x}^{2}$
C.${x}^{2}+{(10-x)}^{2}= {6}^{2}$
D.${x}^{2}+{6}^{2}= {(10-x)}^{2}$
D
)A.${x}^{2}+{6}^{2}= {10}^{2}$
B.${(10-x)}^{2}+{6}^{2}= {x}^{2}$
C.${x}^{2}+{(10-x)}^{2}= {6}^{2}$
D.${x}^{2}+{6}^{2}= {(10-x)}^{2}$
答案:
D
2. 如图,小区物业规划在一个长60 m、宽22 m的矩形场地ABCD上,修建一个小型停车场,阴影部分为停车位所在区域,两侧是宽x m的道路,中间是宽2x m的道路. 如果阴影部分的总面积是$600 m^2,$那么x满足的方程是(
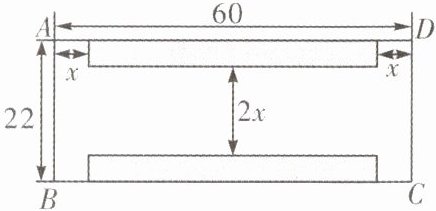
A.${x}^{2}-41x+180= 0$
B.${x}^{2}-41x+225= 0$
C.${x}^{2}-41x+30= 0$
D.${x}^{2}-41x-270= 0$
A
)
A.${x}^{2}-41x+180= 0$
B.${x}^{2}-41x+225= 0$
C.${x}^{2}-41x+30= 0$
D.${x}^{2}-41x-270= 0$
答案:
A
3. 如图,小程的爸爸用一段10 m长的铁丝网围成一个一边靠墙(墙长5.5 m)的矩形鸭舍,其面积为$15 m^2,$在鸭舍侧面中间位置留一个1 m宽的门(由其他材料制成),则BC长为
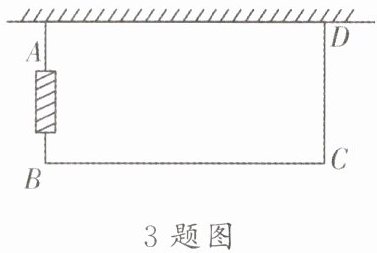
5
m.
答案:
解:设BC长为$x$m,则AB=CD=$\frac{10 + 1 - x}{2}=\frac{11 - x}{2}$m。
依题意,得$x \cdot \frac{11 - x}{2}=15$,
整理,得$x^2 - 11x + 30 = 0$,
解得$x_1 = 5$,$x_2 = 6$。
∵墙长5.5m,$6>5.5$,
∴$x_2 = 6$不合题意,舍去。
∴BC长为5m。
5
依题意,得$x \cdot \frac{11 - x}{2}=15$,
整理,得$x^2 - 11x + 30 = 0$,
解得$x_1 = 5$,$x_2 = 6$。
∵墙长5.5m,$6>5.5$,
∴$x_2 = 6$不合题意,舍去。
∴BC长为5m。
5
4. 如图,有一张矩形纸片,长10 cm、宽6 cm,在它的四个角各剪去一个同样的小正方形,然后将四周突出部分折起,就能制作成一个无盖的方盒,若方盒的底面积是$32 cm^2,$则剪去的小正方形边长为
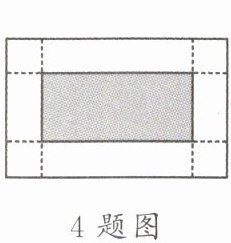
1
cm.
答案:
A(假设选项A代表1,由于题目未给出具体选项内容,此处根据解题过程推断)
5. 某小区有一块长为18 m、宽为6 m的矩形空地,计划在空地中修两块相同的矩形绿地,它们的面积之和为$60 m^2,$两块绿地之间及周边留有宽度相等的人行甬道,求人行甬道的宽度.
]
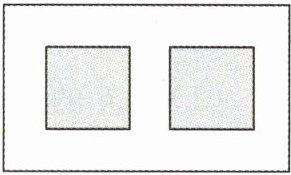
]

答案:
1
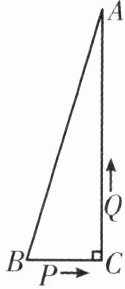
6. 如图,在Rt△ABC中,AC= 24 cm,BC= 7 cm,点P在BC上从B点运动到C点,速度为2 cm/s;点Q在AC上从C点运动到A点,速度为5 cm/s. 若点P、点Q分别从点B、点C同时出发,当P,Q两点中有一个点运动到终点时,则两点均停止运动. 设运动时间为t秒.
(1)当t为何值时P,Q两点间的距离为$5\sqrt{2}\ cm$?
(2)当t为何值时,△PCQ的面积为15 cm^2?
]
(1)当t为何值时P,Q两点间的距离为$5\sqrt{2}\ cm$?
(2)当t为何值时,△PCQ的面积为15 cm^2?
]

答案:
解:由题意得,BP=2t cm,CQ=5t cm。
∵BC=7 cm,AC=24 cm,
∴PC=BC-BP=(7-2t) cm。
∵P到C需7÷2=3.5 s,Q到A需24÷5=4.8 s,
∴t的取值范围为0≤t≤3.5。
(1)在Rt△PCQ中,PC=(7-2t) cm,CQ=5t cm,
由勾股定理得:PC²+CQ²=PQ²,
即(7-2t)²+(5t)²=(5√2)²,
整理得:29t²-28t-1=0,
解得t₁=1,t₂=-1/29(舍去),
∴t=1。
(2)S△PCQ=1/2·PC·CQ=15,
即1/2(7-2t)·5t=15,
整理得:2t²-7t+6=0,
解得t₁=2,t₂=3/2,
∵0≤t≤3.5,
∴t=2或t=3/2。
(1)t=1;
(2)t=2或t=3/2。
∵BC=7 cm,AC=24 cm,
∴PC=BC-BP=(7-2t) cm。
∵P到C需7÷2=3.5 s,Q到A需24÷5=4.8 s,
∴t的取值范围为0≤t≤3.5。
(1)在Rt△PCQ中,PC=(7-2t) cm,CQ=5t cm,
由勾股定理得:PC²+CQ²=PQ²,
即(7-2t)²+(5t)²=(5√2)²,
整理得:29t²-28t-1=0,
解得t₁=1,t₂=-1/29(舍去),
∴t=1。
(2)S△PCQ=1/2·PC·CQ=15,
即1/2(7-2t)·5t=15,
整理得:2t²-7t+6=0,
解得t₁=2,t₂=3/2,
∵0≤t≤3.5,
∴t=2或t=3/2。
(1)t=1;
(2)t=2或t=3/2。
查看更多完整答案,请扫码查看


