《2025年优课堂给力A加九年级数学全一册北师大版》

1. 小华在上午8时、上午9时、上午10时、上午12时四次到室外的阳光下观察向日葵影子的变化情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为(A)
A.上午8时
B.上午9时
C.上午10时
D.上午12时

答案： A

2. 如图,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上投影的长度随着他离墙的距离变小而(B)

A.变大
B.变小
C.不变
D.不能确定

答案： 解：B

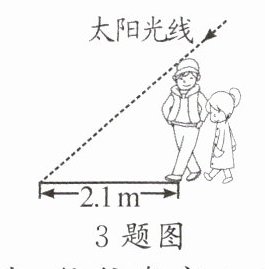
3. 如图,小芳和爸爸正在散步,爸爸身高1.8 m,他在地面上的影长为2.1 m. 若小芳比爸爸矮0.3 m,则她的影长为1.75m.

答案： 1.75

4. 如图,古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔塔顶A的影子A'处直立一根木杆BC,借助太阳光测金字塔的高度. 如图所示,木杆BC长2 m,它的影长BC'是3 m,同一时刻测得OA'是201 m,则金字塔的高度AO是134m.

答案： 134

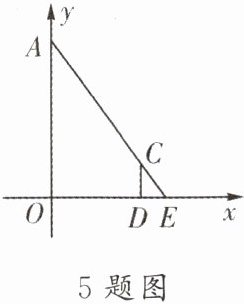
5. 如图,在平面直角坐标系中,一点光源位于A(0,5)处,线段CD⊥x轴,垂足为D,点C的坐标为(3,1),则CD在x轴上的影子长为$\frac{3}{4}$.

答案： 解：设CD在x轴上的影子为DE，E为影子端点。
因为点光源A(0,5)，C(3,1), D(3,0)，
由光的直线传播，A、C、E三点共线。
直线AC的解析式：设y=kx+b，
将A、C代入得：$\begin{cases} b=5 \\ 3k+b=1 \end{cases}$，解得$\begin{cases} k=-\frac{4}{3} \\ b=5 \end{cases}$，
即$y=-\frac{4}{3}x+5$。
令y=0，得$0=-\frac{4}{3}x+5$，解得$x=\frac{15}{4}$。
所以E点坐标为$(\frac{15}{4},0)$，
影子长DE=$\frac{15}{4}-3=\frac{3}{4}$。
$\frac{3}{4}$

6. 如图,甲楼AB高16 m,乙楼CD坐落在甲楼的正北面,已知当地冬至中午12时,物高与影长的比是1:$\sqrt{2}$,甲、乙两楼相距BD为12 m,那么甲楼的影子落在乙楼上的高DE= $16 - 6\sqrt{2}$m.(结果保留根号)

答案： $16 - 6\sqrt{2}$

7. 如图,电线杆的顶上有一盏高为6 m的路灯,电线杆底部为A,身高1.5 m的男孩站在与点A相距6 m的点B处,若男孩以6 m为半径绕电线杆走一圈,则他在路灯下的影子BC扫过的面积为______$m^2$.

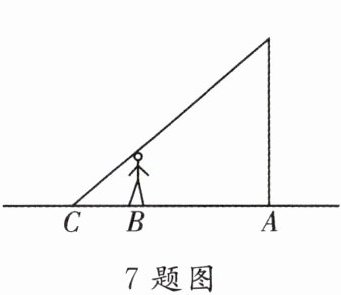
64π

答案： 解：设男孩绕电线杆走一圈时，其头顶在地面的投影点为C，男孩身高为h=1.5m，路灯高为H=6m，男孩与电线杆底部距离AB=6m，男孩行走半径为r=6m。
由相似三角形性质，得 $\frac{h}{H} = \frac{BC}{AC}$，即 $\frac{1.5}{6} = \frac{BC}{AB + BC}$。
解得 $BC = 2m$，则影子端点C到A的距离 $AC = AB + BC = 6 + 2 = 8m$。
影子BC扫过的轨迹是以A为圆心，AC为半径的圆，其面积为 $\pi × 8^2 = 64\pi$ $m^2$。
64π

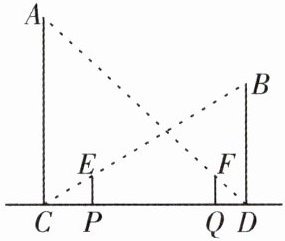
8. 如图,王琳同学在晚上由路灯A走向路灯B,当他走到P处时发现,他在路灯B下的影长为2 m,且恰好位于路灯A的正下方,接着他又走了6.5 m到Q处,此时他在路灯A下的影子恰好位于路灯B的正下方(已知王琳身高1.8 m,路灯B高9 m).
(1)标出王琳站在P处在路灯B下的影子.
(2)计算王琳站在Q处在路灯A下的影长.
(3)计算路灯A的高度.

答案：
(1) 王琳站在P处在路灯B下的影子为线段PC。
(2) 解：设王琳站在Q处在路灯A下的影长QD为x m。
由题意知，△FQD∽△ABD，
则$\frac{FD}{BD} = \frac{QD}{AD}$，即$\frac{1.8}{9} = \frac{x}{x + 6.5 + 2}$，
解得$x = 1.5$。
答：王琳站在Q处在路灯A下的影长为1.5 m。
(3) 解：由
(2)知QD=1.5 m，AD=1.5 + 6.5 + 2=10 m，
△EQC∽△BAC，
则$\frac{EQ}{AB} = \frac{PC}{BC}$，即$\frac{1.8}{AB} = \frac{2}{10}$，
解得AB=9。
答：路灯A的高度为9 m。