《2025年学霸题中题八年级数学上册人教版》

20.（5分）如图，$AB = AC$，点$D$，$E$分别在$AC$，$AB$上，$AG\perp BD$，$AF\perp CE$，垂足分别为$G$，$F$，且$AG = AF$．求证：$AD = AE$．

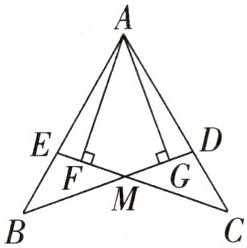
证明：∵$AG⊥BD$，$AF⊥CE$，∴$∠AGB = ∠AFC = 90°$。在$Rt△AGB$和$Rt△AFC$中，$\begin{cases} AB = AC \\ AG = AF \end{cases}$，∴$Rt△AGB≌Rt△AFC$(HL)，∴$∠B = ∠C$。在$△ABD$和$△ACE$中，$\begin{cases} ∠B = ∠C \\ AB = AC \\ ∠BAD = ∠CAE \end{cases}$，∴$△ABD≌△ACE$(ASA)，∴AD = AE。

答案：
∵$AG⊥BD$，$AF⊥CE$，
∴$∠AGB = ∠AFC = 90°$。在$Rt△AGB$和$Rt△AFC$中，$\begin{cases} AB = AC \\ AG = AF \end{cases}$，
∴$Rt△AGB≌Rt△AFC(HL)$，
∴$∠B = ∠C$。在$△ABD$和$△ACE$中，$\begin{cases} ∠B = ∠C \\ AB = AC \\ ∠BAD = ∠CAE \end{cases}$，
∴$△ABD≌△ACE(ASA)$，
∴AD = AE。

21.（8分）如表所示，在平面内，分别用3根、5根、6根火柴（每根火柴长度相等）首尾顺次相接，能搭成不同形状的三角形．
|||
|形状|等边三角形|等腰三角形|等边三角形|
（1）4根火柴首尾顺次相接，能搭成一个三角形吗？不能
（2）8根、12根火柴首尾顺次相接，能搭成几种不同的三角形？分别写出它们的边长．
8根火柴首尾顺次相接能搭成1种三角形，边长分别是3,3,2；12根火柴首尾顺次相接能搭成3种三角形，边长分别是5,4,3或5,5,2或4,4,4。

答案：
(1)不能
(2)8根火柴首尾顺次相接能搭成1种三角形，边长分别是3,3,2；12根火柴首尾顺次相接能搭成3种三角形，边长分别是5,4,3或5,5,2或4,4,4。

22.（8分）如图，$\triangle ABC$中，$\angle ACB = 90^{\circ}$，$AD$平分$\angle BAC$，$DE\perp AB$于$E$．
（1）若$\angle BAC = 50^{\circ}$，求$\angle EDA$的度数；∵$∠BAC = 50°$，AD平分$∠BAC$，∴$∠EAD = \frac{1}{2}∠BAC = 25°$。∵$DE⊥AB$，∴$∠AED = 90°$，∴$∠EDA = 90° - 25° = 65°$。
（2）求证：直线$AD$是线段$CE$的垂直平分线．∵$DE⊥AB$，∴$∠AED = 90° = ∠ACB$。∵AD平分$∠BAC$，∴$∠DAE = ∠DAC$。又∵AD = AD，∴$△AED≌△ACD(AAS)$，∴AE = AC。∵AD平分$∠BAC$，∴$AD⊥CE$，即直线AD是线段CE的垂直平分线。

答案：
(1)
∵$∠BAC = 50°$，AD平分$∠BAC$，
∴$∠EAD = \frac{1}{2}∠BAC = 25°$。
∵$DE⊥AB$，
∴$∠AED = 90°$，
∴$∠EDA = 90° - 25° = 65°$。
(2)
∵$DE⊥AB$，
∴$∠AED = 90° = ∠ACB$。
∵AD平分$∠BAC$，
∴$∠DAE = ∠DAC$。又
∵AD = AD，
∴$△AED≌△ACD(AAS)$，
∴AE = AC。
∵AD平分$∠BAC$，
∴$AD⊥CE$，即直线AD是线段CE的垂直平分线。

23.（10分）如图，在直角坐标系中，$\triangle ABO$的顶点坐标分别为$O(0,0)$，$A(2a,0)$，$B(0,-a)$，线段$EF$两端点坐标分别为$E(-m,a + 1)$，$F(-m,1)(2a ＞ m ＞ a)$．直线$l// y$轴交$x$轴于$P(a,0)$，且线段$EF$与$CD$关于$y$轴对称，线段$CD$与$MN$关于直线$l$对称．
（1）求点$N$，$M$的坐标（用含$m$，$a$的式子表示）．
点$N$的坐标为$(2a - m, 1)$，点$M$的坐标为$(2a - m, a + 1)$。
（2）$\triangle ABO$与$\triangle MFE$通过平移能重合吗？能与不能都要说明其理由，若能，请你说出一个平移方案（平移的单位数用$m$，$a$表示）．
能重合。∵EM = 2a - m - (-m) = 2a = OA，EF = a + 1 - 1 = a = OB，又∵$EF//y$轴，$EM//x$轴，∴$∠MEF = ∠AOB = 90°$，∴$△ABO≌△MFE(SAS)$，∴$△ABO$与$△MFE$通过平移能重合。平移方案不唯一，如：将$△ABO$向上平移(a + 1)个单位长度后，再向左平移m个单位长度，即可重合。

答案：
(1)
∵EF与CD关于y轴对称,EF两端点的坐标分别为E(-m, a + 1)，F(-m, 1)，
∴C(m, a + 1)，D(m, 1)。设CD与直线l之间的距离为x，
∵CD与MN关于直线l对称，l与y轴之间的距离为a，
∴MN与y轴之间的距离为a - x。
∵x = m - a，
∴点M的横坐标为a - (m - a) = 2a - m，
∴M(2a - m, a + 1)，N(2a - m, 1)。
(2)能重合。
∵EM = 2a - m - (-m) = 2a = OA，EF = a + 1 - 1 = a = OB，又
∵$EF//y$轴，$EM//x$轴，
∴$∠MEF = ∠AOB = 90°$，
∴$△ABO≌△MFE(SAS)$，
∴$△ABO$与$△MFE$通过平移能重合。平移方案不唯一，如：将$△ABO$向上平移(a + 1)个单位长度后，再向左平移m个单位长度，即可重合。

24.（8分）如图，在等腰直角三角形$ABC$中，$\angle ACB = 90^{\circ}$，$D$为$BC$的中点，$DE\perp AB$，垂足为$E$，过点$B$作$BF// AC$，交$DE$的延长线于点$F$，连接$CF$，与$AD$交于点$G$．
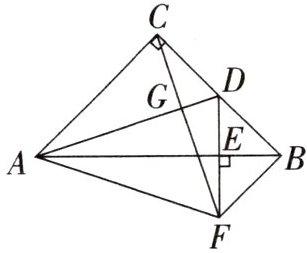
（1）求证：$AD\perp CF$；
在等腰直角三角形ABC中，∵$∠ACB = 90°$，∴$∠CBA = ∠CAB = 45°$。又∵$DE⊥AB$，∴$∠DEB = 90°$，∴$∠BDE = 45°$。又∵$BF//AC$，∴$∠CBF + ∠ACB = 180°$，∴$∠CBF = 90°$，∴$∠BFD = ∠BDE = 45°$，∴BF = DB。∵D为BC的中点，∴CD = DB，∴BF = CD。在$△CBF$和$△ACD$中，BF = CD，$∠CBF = ∠ACD = 90°$，CB = AC，∴$△CBF≌△ACD(SAS)$，∴$∠BCF = ∠CAD$，CF = AD。∵$∠CAD + ∠CDA = 90°$，∴$∠BCF + ∠CDA = 90°$，∴$∠CGD = 90°$，即$AD⊥CF$。
（2）连接$AF$，试判断$\triangle ACF$是否为等腰三角形，并说明理由．
$\triangle ACF$是等腰三角形。理由：由(1)得CF = AD，$△DBF$是等腰直角三角形，且$DE⊥AB$，∴BE垂直平分DF，∴AF = AD，∴CF = AF，∴$△ACF$是等腰三角形。

答案：
(1)在等腰直角三角形ABC中，
∵$∠ACB = 90°$，
∴$∠CBA = ∠CAB = 45°$。又
∵$DE⊥AB$，
∴$∠DEB = 90°$，
∴$∠BDE = 45°$。又
∵$BF//AC$，
∴$∠CBF + ∠ACB = 180°$，
∴$∠CBF = 90°$，
∴$∠BFD = ∠BDE = 45°$，
∴BF = DB。
∵D为BC的中点，
∴CD = DB，
∴BF = CD。在$△CBF$和$△ACD$中，BF = CD，$∠CBF = ∠ACD = 90°$，CB = AC，
∴$△CBF≌△ACD(SAS)$，
∴$∠BCF = ∠CAD$，CF = AD。
∵$∠CAD + ∠CDA = 90°$，
∴$∠BCF + ∠CDA = 90°$，
∴$∠CGD = 90°$，即$AD⊥CF$。
(2)$△ACF$是等腰三角形。理由：由
(1)得CF = AD，$△DBF$是等腰直角三角形，且$DE⊥AB$，
∴BE垂直平分DF，
∴AF = AD，
∴CF = AF，
∴$△ACF$是等腰三角形。