《2025年学霸题中题八年级数学上册人教版》

13. 已知$ 4 ^ { m + 3 } \cdot 8 ^ { m + 1 } ÷ 2 ^ { 4 m + 7 } = 16 $,则$ m = $2.

答案： 2 解析: $ \because 4^{m + 3} \cdot 8^{m + 1} \div 2^{4m + 7} = 16 $，$ \therefore (2^{2})^{m + 3} \cdot (2^{3})^{m + 1} \div 2^{4m + 7} = 16 $，$ \therefore 2^{2m + 6} \cdot 2^{3m + 3} \div 2^{4m + 7} = 16 $，$ \therefore 2^{2m + 6 + 3m + 3 - (4m + 7)} = 2^{4} $，$ \therefore 2^{m + 2} = 2^{4} $，$ \therefore m + 2 = 4 $，$ \therefore m = 2 $。

14. 地球表面平均$ 1 \mathrm { cm } ^ { 2 } $上的空气质量约为1kg,地球的表面积大约是$ 5 \times 10 ^ { 8 } \mathrm { km } ^ { 2 } $,地球的质量约为$ 6 \times 10 ^ { 24 } \mathrm { kg } $.
(1)地球表面上全部空气的质量约为多少千克?
(2)地球的质量大约是其表面上全部空气质量的多少倍? (结果用科学记数法表示)

答案：
(1) 地球表面上全部空气的质量约为 $ 5 \times 10^{8} \times 10^{10} \times 1 = 5 \times 10^{18} $ (kg)。
(2) 地球的质量大约是其表面上全部空气质量的 $ 6 \times 10^{24} \div (5 \times 10^{18}) = 1.2 \times 10^{6} $ 倍。

15. 已知A是一个多项式,单项式B等于2x,某同学计算$ A \div B $时,把$ A \div B $误写成$ A + B $,结果得$ 5 x ^ { 4 } - 4 x ^ { 3 } + 3 x ^ { 2 } $,求$ A \div B $的值.

答案： 根据题意，得 $ A + B = 5x^{4} - 4x^{3} + 3x^{2} $，$ \because B = 2x $，$ \therefore A = 5x^{4} - 4x^{3} + 3x^{2} - 2x $，则 $ A \div B = (5x^{4} - 4x^{3} + 3x^{2} - 2x) \div (2x) = \frac{5}{2}x^{3} - 2x^{2} + \frac{3}{2}x - 1 $。

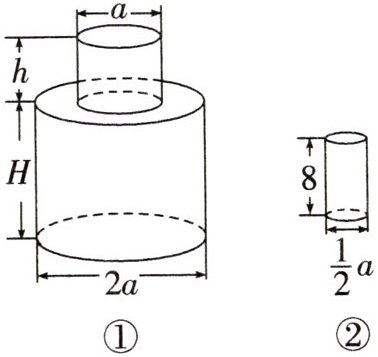
16. 在如图①所示的容器中盛满水,如果将这个容器中的水全部倒入图②的杯子中,那么你知道一共需要多少个这样的杯子吗? (单位:cm)

$\frac{1}{2}h + 2H$

答案： $ \left[ \pi \left( \frac{1}{2}a \right)^{2}h + \pi \left( \frac{1}{2} \times 2a \right)^{2}H \right] \div \left[ \pi \left( \frac{1}{2} \times \frac{1}{2}a \right)^{2} \times 8 \right] = \left( \frac{1}{4}\pi a^{2}h + \pi a^{2}H \right) \div \left( \frac{1}{2}\pi a^{2} \right) = \frac{1}{2}h + 2H $，故一共需要 $ \left( \frac{1}{2}h + 2H \right) $ 个这样的杯子。

17. 阅读下列材料:
$ \because ( x + 3 ) ( x - 2 ) = x ^ { 2 } + x - 6 , \therefore ( x ^ { 2 } + x - 6 ) ÷ ( x - 2 ) = x + 3 $.这说明$ x ^ { 2 } + x - 6 $能被$ ( x - 2 ) $整除,同时也说明多项式$ x ^ { 2 } + x - 6 $有一个因式为$ ( x - 2 ) $,且当$ x = 2 $时,多项式$ x ^ { 2 } + x - 6 $的值为0.
回答下列问题:
(1)根据上面的材料猜想:多项式的值为0、多项式有因式$ ( x - 2 ) $、多项式能被$ ( x - 2 ) $整除,这之间存在着一种什么样的联系?
多项式有因式$(x - 2)$，说明此多项式能被$(x - 2)$整除，另外，当$x = 2$时，此多项式的值为0
(2)探求规律:更一般地,如果一个关于字母x的多项式M,当$ x = k $时,M的值为0,那么M与整式$ ( x - k ) $之间有何种关系?
M能被$(x - k)$整除
(3)应用:利用上面的结果求解,已知$ ( x - 2 ) $能整除$ x ^ { 2 } + k x - 14 $,求k的值.
$ \because (x - 2) $能整除 $ x^{2} + kx - 14 $，$ \therefore $ 当 $ x = 2 $ 时，$ x^{2} + kx - 14 = 0 $，当 $ x = 2 $ 时，$ x^{2} + kx - 14 = 4 + 2k - 14 = 0 $，解得 $ k = 5 $

答案：
(1) 多项式有因式 $ (x - 2) $，说明此多项式能被 $ (x - 2) $ 整除，另外，当 $ x = 2 $ 时，此多项式的值为 0。
(2) 根据
(1) 得出的关系，得出 $ M $ 能被 $ (x - k) $ 整除。
(3) $ \because (x - 2) $ 能整除 $ x^{2} + kx - 14 $，$ \therefore $ 当 $ x = 2 $ 时，$ x^{2} + kx - 14 = 0 $，当 $ x = 2 $ 时，$ x^{2} + kx - 14 = 4 + 2k - 14 = 0 $，解得 $ k = 5 $。