第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
10.(2023·通辽中考)点$Q$的横坐标为一元一次方程$3x + 7 = 32 - 2x$的解,纵坐标为$a + b$的值,其中$a$,$b$满足二元一次方程组$\begin{cases}2a - b = 4,\\ - a + 2b = - 8,\end{cases}$则点$Q$关于$y$轴的对称点$Q'$的坐标为
(−5,−4)
。
答案:
(−5,−4)
11. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 50^{\circ}$,将其折叠,使点$A$落在边$CB$上的$A'$处,折痕为$CD$,则$\angle A'DB$的度数为

10°
。
答案:
10°
12.(益阳中考)如图,在$\triangle ABC$中,$AB = AC$,$\angle BAC = 36^{\circ}$,$DE$是线段$AC$的垂直平分线,若$BE = a$,$AE = b$,则用含$a$,$b$的式子表示$\triangle ABC$的周长为______

2a+3b
。
答案:
2a+3b
13. 如图,$\triangle ABC$是等边三角形,点$E$在$AC$的延长线上,点$D$在线段$AB$上,连接$ED$交线段$BC$于点$F$,过点$F$作$FN\perp AC$于点$N$,$DB = \frac{7}{5}CN$,$EF = FD$,若$FB = 17$,则$AN$的长为______。
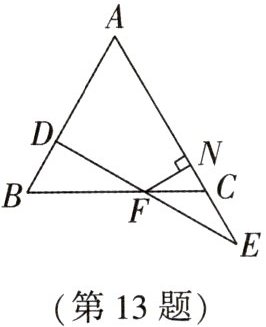

答案:
22 解析:如图,作DG//AC交BC于点G,
∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠BCA=∠BAC=60°,
∴∠DGB=∠ACB=60°,∠DGF=∠ECF。
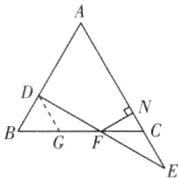
∵∠DFG=∠EFC,DF=EF,
∴△DFG≌△EFC,
∴GF=FC。
∵∠DGB=∠ACB=60°,
∴△BDG是等边三角形,
∴BD=BG。
∵DB=$\frac{7}{5}$CN,
∴设CN=5a,则BD=7a。
∵FN⊥AC,
∴∠NFC=30°,
∴CF=2CN=10a,
∴GF=FC=10a,BD=BG=7a,FB=17a=17,解得a=1,则BC=AC=27a=27,CN=5a=5,AN的长为27−5=22。
22 解析:如图,作DG//AC交BC于点G,
∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠BCA=∠BAC=60°,
∴∠DGB=∠ACB=60°,∠DGF=∠ECF。

∵∠DFG=∠EFC,DF=EF,
∴△DFG≌△EFC,
∴GF=FC。
∵∠DGB=∠ACB=60°,
∴△BDG是等边三角形,
∴BD=BG。
∵DB=$\frac{7}{5}$CN,
∴设CN=5a,则BD=7a。
∵FN⊥AC,
∴∠NFC=30°,
∴CF=2CN=10a,
∴GF=FC=10a,BD=BG=7a,FB=17a=17,解得a=1,则BC=AC=27a=27,CN=5a=5,AN的长为27−5=22。
14. 如图,已知$\angle BAD = \angle DAC = 9^{\circ}$,$AD\perp AE$,且$AB + AC = BE$,则$\angle B =$______

48°
。
答案:
48° 解析:延长BA到点F,使AF=AC,连接EF,
∵AB+AC=BE,
∴AB+AF=BE=BF,
∴∠F=∠BEF=$\frac{1}{2}$(180°−∠B)。
∵∠BAD=∠DAC=9°,AD⊥AE,即∠DAE=90°,
∴∠FAE=180°−(∠BAD+∠DAE)=180°−(9°+90°)=81°,∠CAE=∠DAE−∠DAC=81°,
∴∠FAE=∠CAE。
∵AF=AC,∠FAE=∠CAE,AE=AE,
∴△AFE≌△ACE(SAS),
∴∠F=∠ACE。
∵∠ACE=∠B+∠BAC=∠B+18°,
∴∠F=∠B+18°,
∴∠B+18°=$\frac{1}{2}$×(180°−∠B),则∠B=48°。
∵AB+AC=BE,
∴AB+AF=BE=BF,
∴∠F=∠BEF=$\frac{1}{2}$(180°−∠B)。
∵∠BAD=∠DAC=9°,AD⊥AE,即∠DAE=90°,
∴∠FAE=180°−(∠BAD+∠DAE)=180°−(9°+90°)=81°,∠CAE=∠DAE−∠DAC=81°,
∴∠FAE=∠CAE。
∵AF=AC,∠FAE=∠CAE,AE=AE,
∴△AFE≌△ACE(SAS),
∴∠F=∠ACE。
∵∠ACE=∠B+∠BAC=∠B+18°,
∴∠F=∠B+18°,
∴∠B+18°=$\frac{1}{2}$×(180°−∠B),则∠B=48°。
15.(8分)如图,在平面直角坐标系中,已知$\triangle ABC$的三个顶点的坐标分别为$A(1,0)$,$B(2,-3)$,$C(4,-2)$。
(1)画出$\triangle ABC$关于$x$轴的对称图形$\triangle A_1B_1C_1$;
(2)画出$\triangle A_1B_1C_1$向左平移4个单位长度后得到的$\triangle A_2B_2C_2$;
(3)$\triangle BA_2C_2$的面积为______;
(4)若$AC$上有一点$P(m,n)$经过上述两次变换,则对应$A_2C_2$上的点$P_2$的坐标为______。

(1)画出$\triangle ABC$关于$x$轴的对称图形$\triangle A_1B_1C_1$;
(2)画出$\triangle A_1B_1C_1$向左平移4个单位长度后得到的$\triangle A_2B_2C_2$;
(3)$\triangle BA_2C_2$的面积为______;
(4)若$AC$上有一点$P(m,n)$经过上述两次变换,则对应$A_2C_2$上的点$P_2$的坐标为______。

答案:
(1)如图所示,△A₁B₁C₁即为所求。
(2)如图所示,△A₂B₂C₂即为所求。
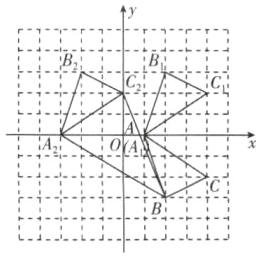
(3)9.5
(4)(m−4,−n)
(1)如图所示,△A₁B₁C₁即为所求。
(2)如图所示,△A₂B₂C₂即为所求。

(3)9.5
(4)(m−4,−n)
16.(5分)(南京中考节选)(1)如图①,要在一条笔直的路边$l$上建一个燃气站,向$l$同侧的$A$,$B$两个城镇分别铺设管道输送燃气。试确定燃气站的位置,使铺设管道的路线最短。
(2)如图②,如果在$A$,$B$两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域,试确定燃气站的位置,使铺设管道的路线最短。

(2)如图②,如果在$A$,$B$两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域,试确定燃气站的位置,使铺设管道的路线最短。

答案:
(1)如图①,点P即为所求。沿AP—PB路线铺设管道,管道长度最短。
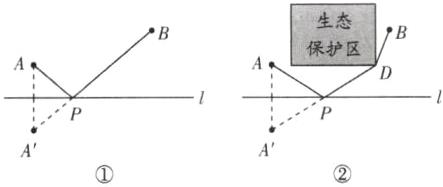
(2)如图②,点P即为所求。
(1)如图①,点P即为所求。沿AP—PB路线铺设管道,管道长度最短。

(2)如图②,点P即为所求。
17.(9分)如图,在$\triangle ABC$中,$\angle ABC = 45^{\circ}$,$CD\perp AB$于点$D$,$AC$的垂直平分线$BE$与$CD$交于点$F$,与$AC$交于点$E$。
(1)判断$\triangle DBC$的形状并说明理由;
(2)求证:$BF = AC$;
(3)试说明:$CE = \frac{1}{2}BF$。
(1)判断$\triangle DBC$的形状并说明理由;
$\triangle DBC$是等腰直角三角形,理由如下:$\because \angle ABC=45^{\circ}$,$CD\perp AB$,$\therefore \angle BCD=\angle ABC=45^{\circ}$,$\therefore BD=CD$,$\therefore \triangle DBC$是等腰直角三角形。
(2)求证:$BF = AC$;
证明:$\because BE\perp AC$,$\therefore \angle BDC=\angle BEC=90^{\circ}$,$\because \angle BFD=\angle CFE$,$\therefore \angle DBF=\angle ACD$。在$\triangle BDF$与$\triangle CDA$中,$\begin{cases}\angle BDF=\angle CDA=90^{\circ}\\BD=CD\\\angle DBF=\angle DCA\end{cases}$,$\therefore \triangle BDF\cong\triangle CDA(ASA)$,$\therefore BF=AC$。
(3)试说明:$CE = \frac{1}{2}BF$。
说明:$\because BE$是$AC$的垂直平分线,$\therefore CE=\frac{1}{2}AC$。由(2)知,$BF=AC$,$\therefore CE=\frac{1}{2}BF$。
答案:
(1)△DBC是等腰直角三角形,理由如下:
∵∠ABC=45°,CD⊥AB,
∴∠BCD=∠ABC=45°,
∴BD=CD,
∴△DBC是等腰直角三角形。
(2)
∵BE⊥AC,
∴∠BDC=∠BEC=90°,
∵∠BFD=∠CFE,
∴∠DBF=∠ACD。在△BDF与△CDA中,$\begin{cases}∠BDF=∠CDA=90°\\BD=CD\\∠DBF=∠DCA\end{cases}$,
∴△BDF≌△CDA(ASA),BF=AC。
(3)
∵BE是AC的垂直平分线,
∴CE=$\frac{1}{2}$AC。由
(2)知,BF=AC,
∴CE=$\frac{1}{2}$BF。
(1)△DBC是等腰直角三角形,理由如下:
∵∠ABC=45°,CD⊥AB,
∴∠BCD=∠ABC=45°,
∴BD=CD,
∴△DBC是等腰直角三角形。
(2)
∵BE⊥AC,
∴∠BDC=∠BEC=90°,
∵∠BFD=∠CFE,
∴∠DBF=∠ACD。在△BDF与△CDA中,$\begin{cases}∠BDF=∠CDA=90°\\BD=CD\\∠DBF=∠DCA\end{cases}$,
∴△BDF≌△CDA(ASA),BF=AC。
(3)
∵BE是AC的垂直平分线,
∴CE=$\frac{1}{2}$AC。由
(2)知,BF=AC,
∴CE=$\frac{1}{2}$BF。
查看更多完整答案,请扫码查看


