第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
10. (2025·河北模拟)如图①是某种型号拉杆箱的实物图,如图②是它的示意图,行李箱的侧面可看成一个长方形,点F,C,D在同一条直线上,为了拉箱时的舒适度,现将$∠ABD$调整为$75^{\circ }$,若$∠D$保持不变,则图中$∠ECF$应 (
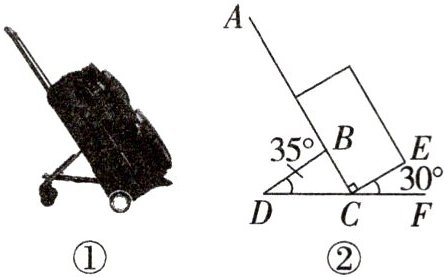
A. 减少$20^{\circ }$
B. 减少$10^{\circ }$
C. 增加$20^{\circ }$
D. 增加$10^{\circ }$
C
)
A. 减少$20^{\circ }$
B. 减少$10^{\circ }$
C. 增加$20^{\circ }$
D. 增加$10^{\circ }$
答案:
C 解析:$\because \angle ABD = 75^{\circ}, \angle D = 35^{\circ}, \therefore \angle BCD = \angle ABD - \angle D = 75^{\circ} - 35^{\circ} = 40^{\circ}. \because \angle ACE = 90^{\circ}, \therefore \angle ECF = 180^{\circ} - \angle BCD - \angle ACE = 180^{\circ} - 40^{\circ} - 90^{\circ} = 50^{\circ}, \therefore 50^{\circ} - 30^{\circ} = 20^{\circ}$,故选 C。
11. (2025·乐山期末)数学兴趣小组同学利用几何图形画出螳螂的简笔画,如图,已知$∠ACB=125^{\circ },∠ADE=70^{\circ }$,且$DE// BC$,则$∠CAD=$____.
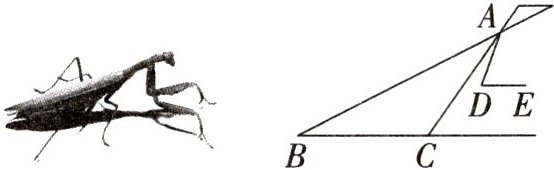

答案:
$15^{\circ}$ 解析:如图,延长 AD 交 BC 于点 F,$\because CB // DE, \therefore \angle ADE = \angle AFH. \because \angle ADE = 70^{\circ}, \therefore \angle AFH = 70^{\circ}. \because \angle BCA = 125^{\circ}, \therefore \angle FCA = 180^{\circ} - \angle BCA = 180^{\circ} - 125^{\circ} = 55^{\circ}. \because \angle AFH$是$\triangle ACF$的外角,$\therefore \angle AFH = \angle CAD + \angle FCA, \therefore 70^{\circ} = \angle CAD + 55^{\circ}, \therefore \angle CAD = 15^{\circ}$。

$15^{\circ}$ 解析:如图,延长 AD 交 BC 于点 F,$\because CB // DE, \therefore \angle ADE = \angle AFH. \because \angle ADE = 70^{\circ}, \therefore \angle AFH = 70^{\circ}. \because \angle BCA = 125^{\circ}, \therefore \angle FCA = 180^{\circ} - \angle BCA = 180^{\circ} - 125^{\circ} = 55^{\circ}. \because \angle AFH$是$\triangle ACF$的外角,$\therefore \angle AFH = \angle CAD + \angle FCA, \therefore 70^{\circ} = \angle CAD + 55^{\circ}, \therefore \angle CAD = 15^{\circ}$。

12. (2025·成都期末)如图,点E是$\triangle ABC$的外角$∠CBD$内部一点,满足$∠CAB=3∠EAB,∠CBD=3∠EBD$.若$∠C=42^{\circ }$,则$∠E$的度数是____
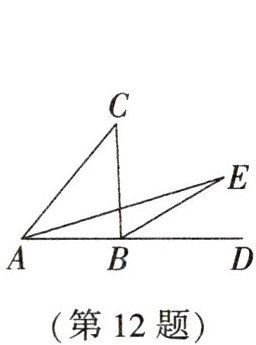
14°
.
答案:
$14^{\circ}$ 解析:设$\angle EAB = x, \angle EBD = y, \because \angle CAB = 3\angle EAB, \angle CBD = 3\angle EBD, \therefore \angle CAB = 3x, \angle CBD = 3y. \because \angle EBD = \angle EAB + \angle E$,$\angle CBD = \angle CAB + \angle C, \therefore y = x + \angle E$ ①,$3y = 3x + \angle C$ ②。$\because \angle C = 42^{\circ}, \therefore$由①②,得$\angle E + x = \frac{1}{3} \times 42^{\circ} + x$,解得$\angle E = 14^{\circ}$。
13. (2024·荆门期中)如图,在$\triangle ABC$中,BD,BE分别是高和角平分线,点F在CA的延长线上,$FH⊥BE$交BD于G,交BC于H,下列结论:①$∠DBE=∠F$;②$2∠BEF=∠BAF-∠C$;③$∠F=\frac {1}{2}(∠BAC-∠C)$;④$∠BGH=∠ABE+∠C$.正确的序号是____
①③④
.
答案:
①③④ 解析:①$\because BD \perp FD, \therefore \angle FGD + \angle F = 90^{\circ}$。$\because FH \perp BE, \therefore \angle BGH + \angle DBE = 90^{\circ}$。$\because \angle FGD = \angle BGH, \therefore \angle DBE = \angle F$,①正确;②$\because BE$平分$\angle ABC, \therefore \angle ABE = \angle CBE. \because \angle BEF = \angle CBE + \angle C, \therefore 2\angle BEF = 2(\angle CBE + \angle C) = \angle ABC + 2\angle C. \because \angle BAF = \angle ABC + \angle C, \therefore 2\angle BEF = \angle BAF + \angle C$,②错误;③$\because \angle ABD = 90^{\circ} - \angle BAC, \therefore \angle DBE = \angle ABE - \angle ABD = \angle ABE - 90^{\circ} + \angle BAC = \angle CBE - 90^{\circ} + \angle BAC = \angle CBD - \angle DBE - 90^{\circ} + \angle BAC$。$\because \angle CBD = 90^{\circ} - \angle C, \therefore \angle DBE = \angle BAC - \angle C - \angle DBE, \therefore \angle DBE = \frac{1}{2}(\angle BAC - \angle C)$,由①得,$\angle DBE = \angle F, \therefore \angle F = \frac{1}{2}(\angle BAC - \angle C)$,③正确;④$\because \angle AEB = \angle EBC + \angle C, \angle ABE = \angle CBE, \therefore \angle AEB = \angle ABE + \angle C$。$\because BD \perp FC, FH \perp BE, \therefore \angle FGD = \angle FEB$。$\because \angle FGD = \angle BGH, \therefore \angle BGH = \angle FGD = \angle AEB = \angle ABE + \angle C$,④正确,故正确的序号是①③④。
14. 已知:射线CP是$\triangle ABC$的外角$∠ACD$的平分线.
(1)如图①,延长BA交射线CP于点E,若$∠B=35^{\circ },∠BEC=29^{\circ }$,求$∠BAC$的度数;
(2)如图②,射线BF交CP于点G,若$∠BAC=2∠BGC$,求证:BF平分$∠ABC$.
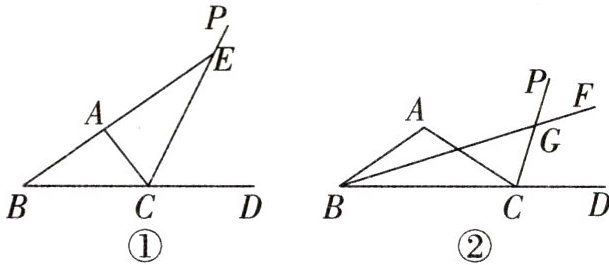
(1)如图①,延长BA交射线CP于点E,若$∠B=35^{\circ },∠BEC=29^{\circ }$,求$∠BAC$的度数;
(2)如图②,射线BF交CP于点G,若$∠BAC=2∠BGC$,求证:BF平分$∠ABC$.

答案:
(1)$\because \angle B = 35^{\circ}, \angle BEC = 29^{\circ}, \therefore \angle DCE = \angle B + \angle BEC = 35^{\circ} + 29^{\circ} = 64^{\circ}. \because$射线 CP 是$\triangle ABC$的外角$\angle ACD$的平分线,$\therefore \angle ACE = \angle DCE = 64^{\circ}, \therefore \angle BAC = \angle BEC + \angle ACE = 29^{\circ} + 64^{\circ} = 93^{\circ}$。
(2)$\because$射线 CP 是$\triangle ABC$的外角$\angle ACD$的平分线,$\therefore \angle ACD = 2\angle GCD. \because \angle GCD = \angle GBC + \angle BGC, \therefore \angle ACD = 2\angle GCD = 2\angle GBC + 2\angle BGC. \because \angle BAC = 2\angle BGC, \therefore \angle ACD = 2\angle GBC + \angle BAC. \because \angle ACD = \angle ABC + \angle BAC, \therefore \angle ABC = 2\angle GBC, \therefore BF$平分$\angle ABC$。
归纳总结
双角平分线模型:
双内角平分线:如图,在$\triangle ABC$中,BP 平分$\angle ABC$,CP 平分$\angle ACB$,则$\angle P = 90^{\circ} + \frac{1}{2}\angle A$。
双外角平分线:如图,BP 平分$\angle CBF$,CP 平分$\angle BCE$,则$\angle P = 90^{\circ} - \frac{1}{2}\angle A$。
一内角一外角平分线:如图,在$\triangle ABC$中,BP 平分$\angle ABC$,CP 平分$\angle ACE$,则$\angle P = \frac{1}{2}\angle A$。

(1)$\because \angle B = 35^{\circ}, \angle BEC = 29^{\circ}, \therefore \angle DCE = \angle B + \angle BEC = 35^{\circ} + 29^{\circ} = 64^{\circ}. \because$射线 CP 是$\triangle ABC$的外角$\angle ACD$的平分线,$\therefore \angle ACE = \angle DCE = 64^{\circ}, \therefore \angle BAC = \angle BEC + \angle ACE = 29^{\circ} + 64^{\circ} = 93^{\circ}$。
(2)$\because$射线 CP 是$\triangle ABC$的外角$\angle ACD$的平分线,$\therefore \angle ACD = 2\angle GCD. \because \angle GCD = \angle GBC + \angle BGC, \therefore \angle ACD = 2\angle GCD = 2\angle GBC + 2\angle BGC. \because \angle BAC = 2\angle BGC, \therefore \angle ACD = 2\angle GBC + \angle BAC. \because \angle ACD = \angle ABC + \angle BAC, \therefore \angle ABC = 2\angle GBC, \therefore BF$平分$\angle ABC$。
归纳总结
双角平分线模型:
双内角平分线:如图,在$\triangle ABC$中,BP 平分$\angle ABC$,CP 平分$\angle ACB$,则$\angle P = 90^{\circ} + \frac{1}{2}\angle A$。
双外角平分线:如图,BP 平分$\angle CBF$,CP 平分$\angle BCE$,则$\angle P = 90^{\circ} - \frac{1}{2}\angle A$。
一内角一外角平分线:如图,在$\triangle ABC$中,BP 平分$\angle ABC$,CP 平分$\angle ACE$,则$\angle P = \frac{1}{2}\angle A$。

15. (1)如图①,在$\triangle ADC$中,$∠ADC$的平分线和$∠ACD$的外角平分线交于点P,若$∠ADC=70^{\circ },∠ACD=50^{\circ }$,求$∠P$的度数;
(2)如图②,在四边形ABCD中,$∠ADC$的平分线和$∠BCD$的外角平分线交于点P,$∠A=90^{\circ },∠B=150^{\circ }$,求$∠P$的度数;
(3)如图③,若将(2)中“$∠A=90^{\circ },∠B=150^{\circ }$”改为“$∠A=α,∠B=β$”,其余条件不变,直接写出$∠P$与$α+β$之间的数量关系.
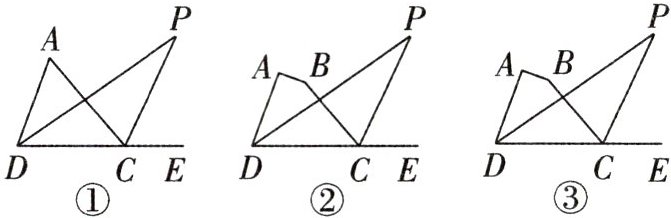
(2)如图②,在四边形ABCD中,$∠ADC$的平分线和$∠BCD$的外角平分线交于点P,$∠A=90^{\circ },∠B=150^{\circ }$,求$∠P$的度数;
(3)如图③,若将(2)中“$∠A=90^{\circ },∠B=150^{\circ }$”改为“$∠A=α,∠B=β$”,其余条件不变,直接写出$∠P$与$α+β$之间的数量关系.

答案:
(1) 如图①。$\because DP$平分$\angle ADC, \therefore \angle PDC = \frac{1}{2}\angle ADC = 35^{\circ}$。$\because \angle ACD = 50^{\circ}, \therefore \angle ACE = 180^{\circ} - \angle ACD = 130^{\circ}. \because CP$平分$\angle ACE, \therefore \angle PCE = \frac{1}{2}\angle ACE = 65^{\circ}. \therefore \angle P = \angle PCE - \angle PDC = 30^{\circ}$。

(2) 如图②所示,延长 DA 交 CB 的延长线于 F。$\because \angle DAB = 90^{\circ}, \therefore \angle BAF = 90^{\circ}. \because \angle ABC = 150^{\circ}, \therefore \angle F = \angle ABC - \angle BAF = 60^{\circ}. \because DP$平分$\angle FDC, \therefore \angle PDC = \frac{1}{2}\angle FDC. \because CP$平分$\angle FCE, \therefore \angle PCE = \frac{1}{2}\angle FCE. \because \angle FCE = \angle F + \angle FDC, \angle PCE = \angle P + \angle PDC, \therefore \angle P = \angle PCE - \angle PDC = \frac{1}{2}\angle F + \angle PDC - \angle PDC = \frac{1}{2}\angle F = 30^{\circ}$。
(3)$\alpha + \beta = 2\angle P + 180^{\circ}$。解析:如图②所示,$\because \angle DAB = \alpha, \therefore \angle BAF = 180^{\circ} - \angle DAB = 180^{\circ} - \alpha. \because \angle ABC = \beta, \therefore \angle F = \angle ABC - \angle BAF = \alpha + \beta - 180^{\circ}. \because DP$平分$\angle FDC, \therefore \angle PDC = \frac{1}{2}\angle FDC. \because CP$平分$\angle FCE, \therefore \angle PCE = \frac{1}{2}\angle FCE. \because \angle FCE = \angle F + \angle FDC, \angle PCE = \angle P + \angle PDC, \therefore \angle P = \angle PCE - \angle PDC = \frac{1}{2}\angle F + \angle PDC - \angle PDC = \frac{1}{2}\angle F = \frac{1}{2}(\alpha + \beta) - 90^{\circ}, \therefore \alpha + \beta = 2\angle P + 180^{\circ}$。
(1) 如图①。$\because DP$平分$\angle ADC, \therefore \angle PDC = \frac{1}{2}\angle ADC = 35^{\circ}$。$\because \angle ACD = 50^{\circ}, \therefore \angle ACE = 180^{\circ} - \angle ACD = 130^{\circ}. \because CP$平分$\angle ACE, \therefore \angle PCE = \frac{1}{2}\angle ACE = 65^{\circ}. \therefore \angle P = \angle PCE - \angle PDC = 30^{\circ}$。

(2) 如图②所示,延长 DA 交 CB 的延长线于 F。$\because \angle DAB = 90^{\circ}, \therefore \angle BAF = 90^{\circ}. \because \angle ABC = 150^{\circ}, \therefore \angle F = \angle ABC - \angle BAF = 60^{\circ}. \because DP$平分$\angle FDC, \therefore \angle PDC = \frac{1}{2}\angle FDC. \because CP$平分$\angle FCE, \therefore \angle PCE = \frac{1}{2}\angle FCE. \because \angle FCE = \angle F + \angle FDC, \angle PCE = \angle P + \angle PDC, \therefore \angle P = \angle PCE - \angle PDC = \frac{1}{2}\angle F + \angle PDC - \angle PDC = \frac{1}{2}\angle F = 30^{\circ}$。
(3)$\alpha + \beta = 2\angle P + 180^{\circ}$。解析:如图②所示,$\because \angle DAB = \alpha, \therefore \angle BAF = 180^{\circ} - \angle DAB = 180^{\circ} - \alpha. \because \angle ABC = \beta, \therefore \angle F = \angle ABC - \angle BAF = \alpha + \beta - 180^{\circ}. \because DP$平分$\angle FDC, \therefore \angle PDC = \frac{1}{2}\angle FDC. \because CP$平分$\angle FCE, \therefore \angle PCE = \frac{1}{2}\angle FCE. \because \angle FCE = \angle F + \angle FDC, \angle PCE = \angle P + \angle PDC, \therefore \angle P = \angle PCE - \angle PDC = \frac{1}{2}\angle F + \angle PDC - \angle PDC = \frac{1}{2}\angle F = \frac{1}{2}(\alpha + \beta) - 90^{\circ}, \therefore \alpha + \beta = 2\angle P + 180^{\circ}$。
查看更多完整答案,请扫码查看


