《2025年学霸题中题八年级数学上册人教版》

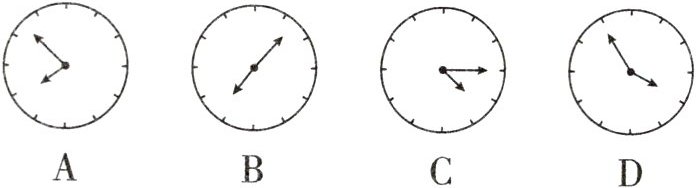
10. 如下是小华在镜中看到身后墙上的钟,则实际时间最接近8点的是 (D)

答案： D　解析:根据镜面对称的性质，在平面镜中的钟面上的时针、分针的位置和实物应关于过12时、6时的直线成轴对称.8点的对称点是4点，那么8点的时钟在镜子中看来应该是4点的样子.

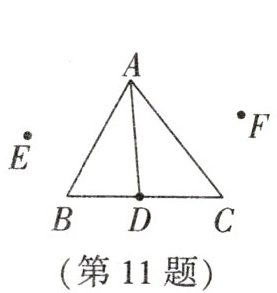
11. 改编题 如图,$ \triangle ABC $中,$ D $点在$ BC $上,点$ D $关于$ AB $,$ AC $的对称点分别是点$ E $,$ F $.
(1)若$ \angle ABC = 62^\circ $,$ \angle ACD = 51^\circ $,则$ \angle EAF = $134$ ^\circ $.
(2)若$ AD = 2.8 $,则$ EF $的取值范围是$0＜EF≤5.6$.

答案：
(1)134　
(2)$0＜EF≤5.6$

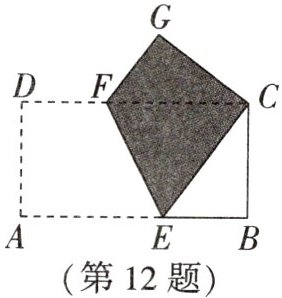
12. 改编题 如图,将长方形纸片$ ABCD $沿$ EF $折叠,使点$ A $与点$ C $重合,点$ D $落在点$ G $处,$ EF $为折痕.
(1)若$ \angle EFC = 65^\circ $,则$ \angle CEB = $50$ ^\circ $.
(2)若$ AB = 8 $,$ AD = 4 $,则$ \triangle CFG $的周长是12,四边形$ CEFG $的面积是16.

答案：
(1)50
(2)12 16 解析:由折叠可知,$GF=DF,△CFG$的周长$=GF+FC+CG=AB+AD=12$;易得$△FGC\cong △EBC$,
∴ 四边形ECGF的面积=四边形EADF的面积=四边形EBCF的面积=四边形ABCD面积的一半,$\therefore S_{四边形CEFG}=4×8÷2=16$.

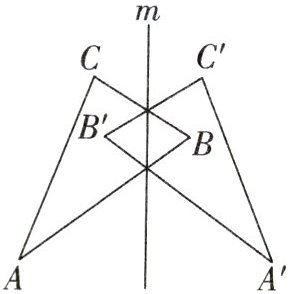
13. 教材P71习题T11变式 如图$, \triangle ABC $和$ \triangle A'B'C' $关于直线 m 对称.
(1)结合图形写出对称点.对称点有A和A',B和B',C和C'.
$(2) \triangle ABC $和$ \triangle A'B'C' $有什么关系?若$ \angle A = 32^\circ , \angle B' = 68^\circ ,$求$ \angle C' $的度数.由题意$△ABC\cong △A'B'C'($合理即可).在△A'B'C'中$,∠A'=∠A=32^{\circ },\therefore ∠C'=180^{\circ }-∠A'-∠B'=180^{\circ }-32^{\circ }-68^{\circ }=80^{\circ }.$
(3)分别连接 AA' , BB' , CC' ,直线 m 与线段 AA' , BB' , CC' 有什么关系?线段 AA' , BB' , CC' 之间有什么关系?直线m垂直平分线段AA',BB',CC',AA'// BB'// CC'.(4)延长线段 AC 与 A'C' ,它们的交点与直线 m 有怎样的关系?其他对应线段(或其延长线)的交点呢?你发现了什么规律,请叙述出来与同伴交流.延长线段AC与A'C',它们的交点在直线m上,其他对应线段(或其延长线)的交点也在直线m上.规律:若两条线段关于直线m对称,且不平行,则它们的交点或它们的延长线的交点在对称轴m上.(合理即可)

答案：
(1)对称点有A和$A',B$和$B',C$和$C'.$
(2)由题意$△ABC\cong △A'B'C'$(合理即可).
在$△A'B'C'$中,$∠A'=∠A=32^{\circ },\therefore ∠C'=180^{\circ }-∠A'-∠B'=180^{\circ }-32^{\circ }-68^{\circ }=80^{\circ }.$
(3)直线m垂直平分线段$AA',BB',CC',AA'// BB'// CC'.$
(4)延长线段AC与$A'C'$,它们的交点在直线m上,其他对应线段(或其延长线)的交点也在直线m上.规律:若两条线段关于直线m对称,且不平行,则它们的交点或它们的延长线的交点在对称轴m上.(合理即可)

14. 原创题 我们把公历纪年日期中数字左右完全对称的日期,称为“完全对称日”,如下一个“完全对称日”是2030年03月02日,它可以用数字写为20300302,则21世纪一共有12个“完全对称日”.

答案： 12　解析:“完全对称日”的结构为:年份+2位数月份+2位数日期,21世纪的“完全对称日”格式为20XXXX02,开头两个数字与最后两个数字都是固定的,只需要考虑中间4个数字即可.因为月份为01,02,03,04,05,06,07,08,09,10,11,12,根据对称可知年份的后两位为10,20,30,40,50,60,70,80,90,01,11,21,共12个.

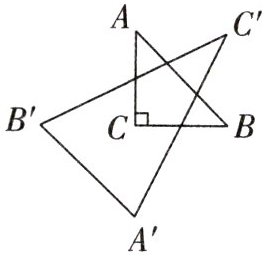
15. 如图,在$ \triangle ABC $中,$ \angle C = 90^\circ $,点$ A $关于$ BC $边所在直线的对称点为$ A' $,点$ B $关于$ AC $边所在直线的对称点为$ B' $,点$ C $关于$ AB $边所在直线的对称点为$ C' $,则$ S_{\triangle ABC} $与$ S_{\triangle A'B'C'} $的比值是多少?

答案：
如图,连接$C'C$交AB于点E,并延长$C'C$交$A'B'$于点D,连接$CB',CA',AC'$.由题意得$AC=A'C,BC=B'C,∠ACB=∠A'CB',AB$垂直平分$CC',\therefore △ABC\cong △A'B'C(SAS),\therefore S_{△ABC}=S_{△A'B'C},∠BAC=∠AA'B',AB=A'B',\therefore AB// A'B',\therefore CD⊥A'B',\therefore $根据全等三角形对应边上的高相等,可得$CD=CE,\therefore CD=CE=EC',\therefore S_{△A'B'C}=\frac {1}{3}S_{△A'B'C'},\therefore S_{△ABC}=\frac {1}{3}S_{△A'B'C'},\therefore S_{△ABC}$与$S_{△A'B'C'}$的比值为$\frac {1}{3}$.