第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
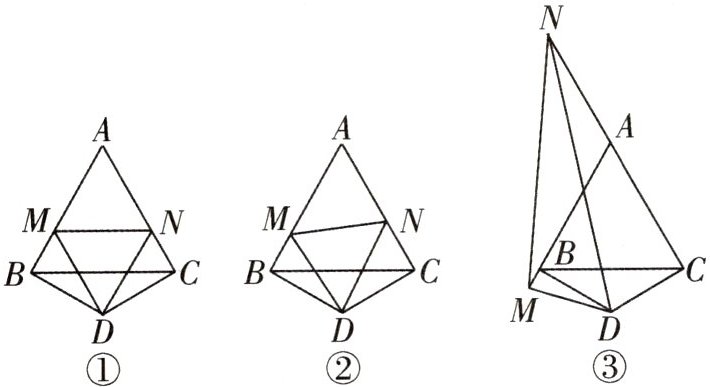
9. 在等边$\triangle ABC$的两边$AB$,$AC$所在直线上分别有两点$M$,$N$,$D$为$\triangle ABC$外一点,且$\angle MDN = 60^{\circ}$,$\angle BDC = 120^{\circ}$,$BD = DC$. 探究:当$M$,$N$分别在直线$AB$,$AC$上移动时,$BM$,$NC$,$MN$之间的数量关系及$\triangle AMN$的周长$Q$与等边$\triangle ABC$的周长$L$的关系.
(1) 如图①所示,当点$M$,$N$在边$AB$,$AC$上,且$DM = DN$时,$BM$,$NC$,$MN$之间的数量关系是____;此时$\frac{Q}{L} = $____.(不必证明)
(2) 如图②所示,点$M$,$N$在边$AB$,$AC$上,且当$DM \neq DN$时,猜想(1)问的两个结论还成立吗? 写出你的猜想并加以证明.
(3) 如图③所示,当$M$,$N$分别在边$AB$,$CA$的延长线上时,猜想$BM$,$NC$,$MN$之间的数量关系并加以证明.
(4) 在(3)问的条件下,若此时$AN = x$,则$Q = $____(用含有$x$,$L$的式子表示).
(1) 如图①所示,当点$M$,$N$在边$AB$,$AC$上,且$DM = DN$时,$BM$,$NC$,$MN$之间的数量关系是____;此时$\frac{Q}{L} = $____.(不必证明)
(2) 如图②所示,点$M$,$N$在边$AB$,$AC$上,且当$DM \neq DN$时,猜想(1)问的两个结论还成立吗? 写出你的猜想并加以证明.
(3) 如图③所示,当$M$,$N$分别在边$AB$,$CA$的延长线上时,猜想$BM$,$NC$,$MN$之间的数量关系并加以证明.
(4) 在(3)问的条件下,若此时$AN = x$,则$Q = $____(用含有$x$,$L$的式子表示).

答案:
(1) $BM + NC = MN$ $\frac{2}{3}$
(2)
(1) 问的两个结论仍然成立。证明:如图①,在 $AC$ 的延长线上截取 $CP = BM$,连接 $DP$,在等边 $\triangle ABC$ 中,$\angle ABC = \angle ACB = 60^{\circ}$。$\because \angle BDC = 120^{\circ}$,$BD = DC$,$\therefore \angle DBC = \angle DCB = 30^{\circ}$,
$\therefore \angle DBM = \angle DCP = 90^{\circ}$。在 $\triangle DBM$ 与 $\triangle DCP$ 中,
$\begin{cases}BM = CP,\\\angle DBM = \angle DCP,\\BD = CD,\end{cases}$ $\therefore \triangle DBM \cong \triangle DCP(SAS)$,
$\therefore \angle BDM = \angle CDP$,$DM = DP$。$\because \angle BDC = 120^{\circ}$,$\angle MDN = 60^{\circ}$,
$\therefore \angle PDN = \angle CDP + \angle CDN = \angle BDM + \angle CDN = 120^{\circ} - 60^{\circ} = 60^{\circ}$。在 $\triangle DMN$ 与 $\triangle DPN$ 中,$\begin{cases}DM = DP,\\\angle MDN = \angle PDN,\\DN = DN,\end{cases}$ $\therefore \triangle DMN \cong \triangle DPN(SAS)$,
$\therefore MN = PN = NC + PC = NC + BM$,$\therefore Q = AM + MN + AN = (AM + BM) + (CN + AN) = AB + AC = 2AB$。$\because L = AB + AC + BC = 3AB$,
$\therefore \frac{Q}{L} = \frac{2}{3}$。
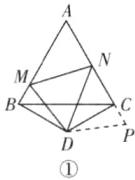
(3) $CN = BM + MN$。证明:如图②,在 $NC$ 上截取 $CH = BM$,连接 $DH$,由
(2) 知,$\angle ABD = \angle ACD = 90^{\circ}$,
$\therefore \angle MBD = 180^{\circ} - 90^{\circ} = 90^{\circ}$。在 $\triangle DBM$ 和 $\triangle DCH$ 中,$\begin{cases}BD = CD,\\\angle DBM = \angle DCH,\\BM = CH,\end{cases}$ $\therefore \triangle DBM \cong \triangle DCH(SAS)$,
$\therefore \angle BDM = \angle CDH$,$DM = DH$。
$\because \angle MDN = \angle BDM + \angle BDN = \angle CDH + \angle BDN = 60^{\circ}$,$\angle BDC = 120^{\circ}$,
$\therefore \angle NDH = 60^{\circ}$。在 $\triangle MDN$ 和 $\triangle HDN$ 中,$\begin{cases}MD = HD,\\\angle MDN = \angle HDN,\\DN = DN,\end{cases}$
$\therefore \triangle MDN \cong \triangle HDN(SAS)$,$\therefore MN = HN$。$\because CN = NH + CH$,$CH = BM$,
$\therefore CN = BM + MN$。
(4) $2x + \frac{2}{3}L$ 解析:$\triangle AMN$ 的周长 $Q = AN + AM + MN = AN + AB + BM + AN + AC - BM = 2AN + 2AB$。$\because AN = x$,$AB = \frac{1}{3}L$,$\therefore Q = 2x + \frac{2}{3}L$。
(1) $BM + NC = MN$ $\frac{2}{3}$
(2)
(1) 问的两个结论仍然成立。证明:如图①,在 $AC$ 的延长线上截取 $CP = BM$,连接 $DP$,在等边 $\triangle ABC$ 中,$\angle ABC = \angle ACB = 60^{\circ}$。$\because \angle BDC = 120^{\circ}$,$BD = DC$,$\therefore \angle DBC = \angle DCB = 30^{\circ}$,
$\therefore \angle DBM = \angle DCP = 90^{\circ}$。在 $\triangle DBM$ 与 $\triangle DCP$ 中,
$\begin{cases}BM = CP,\\\angle DBM = \angle DCP,\\BD = CD,\end{cases}$ $\therefore \triangle DBM \cong \triangle DCP(SAS)$,
$\therefore \angle BDM = \angle CDP$,$DM = DP$。$\because \angle BDC = 120^{\circ}$,$\angle MDN = 60^{\circ}$,
$\therefore \angle PDN = \angle CDP + \angle CDN = \angle BDM + \angle CDN = 120^{\circ} - 60^{\circ} = 60^{\circ}$。在 $\triangle DMN$ 与 $\triangle DPN$ 中,$\begin{cases}DM = DP,\\\angle MDN = \angle PDN,\\DN = DN,\end{cases}$ $\therefore \triangle DMN \cong \triangle DPN(SAS)$,
$\therefore MN = PN = NC + PC = NC + BM$,$\therefore Q = AM + MN + AN = (AM + BM) + (CN + AN) = AB + AC = 2AB$。$\because L = AB + AC + BC = 3AB$,
$\therefore \frac{Q}{L} = \frac{2}{3}$。

(3) $CN = BM + MN$。证明:如图②,在 $NC$ 上截取 $CH = BM$,连接 $DH$,由
(2) 知,$\angle ABD = \angle ACD = 90^{\circ}$,
$\therefore \angle MBD = 180^{\circ} - 90^{\circ} = 90^{\circ}$。在 $\triangle DBM$ 和 $\triangle DCH$ 中,$\begin{cases}BD = CD,\\\angle DBM = \angle DCH,\\BM = CH,\end{cases}$ $\therefore \triangle DBM \cong \triangle DCH(SAS)$,
$\therefore \angle BDM = \angle CDH$,$DM = DH$。
$\because \angle MDN = \angle BDM + \angle BDN = \angle CDH + \angle BDN = 60^{\circ}$,$\angle BDC = 120^{\circ}$,
$\therefore \angle NDH = 60^{\circ}$。在 $\triangle MDN$ 和 $\triangle HDN$ 中,$\begin{cases}MD = HD,\\\angle MDN = \angle HDN,\\DN = DN,\end{cases}$
$\therefore \triangle MDN \cong \triangle HDN(SAS)$,$\therefore MN = HN$。$\because CN = NH + CH$,$CH = BM$,
$\therefore CN = BM + MN$。
(4) $2x + \frac{2}{3}L$ 解析:$\triangle AMN$ 的周长 $Q = AN + AM + MN = AN + AB + BM + AN + AC - BM = 2AN + 2AB$。$\because AN = x$,$AB = \frac{1}{3}L$,$\therefore Q = 2x + \frac{2}{3}L$。
10. 如图,在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,点$D$,$E$在边$BC$上,$\angle CAE = \angle B$,$E$是$CD$的中点,且$AD$平分$\angle BAE$,试问:$BD$与$AC$相等吗? 请说说你的理由.


答案:
$BD = AC$。理由如下:如图,由于 $AD$ 平分 $\angle BAE$,可将 $\triangle ABD$ 沿 $AD$ 所在直线翻折到 $\triangle AFD$ 的位置,则 $\triangle ABD \cong \triangle AFD$,$\therefore \angle F = \angle B$,$BD = DF$。又 $\because \angle CAE = \angle B$,$\therefore \angle CAE = \angle F$。又 $\because \angle AEC = \angle FED$,且 $E$ 是 $CD$ 的中点,$\therefore \triangle ACE \cong \triangle FDE$,
$\therefore DF = AC$,$\therefore BD = AC$。

$BD = AC$。理由如下:如图,由于 $AD$ 平分 $\angle BAE$,可将 $\triangle ABD$ 沿 $AD$ 所在直线翻折到 $\triangle AFD$ 的位置,则 $\triangle ABD \cong \triangle AFD$,$\therefore \angle F = \angle B$,$BD = DF$。又 $\because \angle CAE = \angle B$,$\therefore \angle CAE = \angle F$。又 $\because \angle AEC = \angle FED$,且 $E$ 是 $CD$ 的中点,$\therefore \triangle ACE \cong \triangle FDE$,
$\therefore DF = AC$,$\therefore BD = AC$。

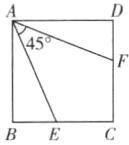
11. 如图,正方形$ABCD$中,点$E$是$BC$上一点,点$F$是$DC$上一点,$\angle EAF = 45^{\circ}$.
(1) 如图①,若$BE = DF = 1$,求$EF$的长;
(2) 如图②,求证:$BE + DF = EF$;
(3) 如图③,点$E$为$CB$延长线上一点,点$F$为$DC$延长线上一点,$\angle EAF = 45^{\circ}$.请直接写出线段$BE$,$DF$,$EF$的数量关系.

(1) 如图①,若$BE = DF = 1$,求$EF$的长;
(2) 如图②,求证:$BE + DF = EF$;
(3) 如图③,点$E$为$CB$延长线上一点,点$F$为$DC$延长线上一点,$\angle EAF = 45^{\circ}$.请直接写出线段$BE$,$DF$,$EF$的数量关系.

答案:
(1) 如图①,将 $\triangle ADF$ 绕着点 $A$ 按顺时针方向旋转 $90^{\circ}$,得 $\triangle ABH$。
$\because$ 四边形 $ABCD$ 是正方形,$\therefore AD = AB = BC = CD$,$\angle ABC = \angle ADF = \angle C = 90^{\circ}$。$\because DF = BE = BH = 1$,由旋转可得 $AF = AH$,$\angle DAF = \angle BAH$。
$\because \angle EAF = 45^{\circ}$,$\therefore \angle DAF + \angle BAE = 45^{\circ} = \angle BAH + \angle BAE = \angle HAE = \angle EAF$。又 $\because AE = AE$,$\therefore \triangle AEF \cong \triangle AEH(SAS)$,$\therefore HE = EF = 2$。

(2) 将 $\triangle ADF$ 绕着点 $A$ 按顺时针方向旋转 $90^{\circ}$,得 $\triangle ABF'$,如图②,则 $\angle ABF' = \angle D$,$AF = AF'$,$\angle BAF' = \angle DAF$。$\because$ 四边形 $ABCD$ 是正方形,$\therefore \angle D = \angle ABC = 90^{\circ}$,$\therefore \angle ABF' = 90^{\circ}$,$\therefore \angle F'BC = 180^{\circ}$,$\therefore$ 点 $F'$,$B$,$E$ 在一条直线上。$\because \angle EAF = 45^{\circ}$,$\therefore \angle DAF + \angle BAE = 45^{\circ} = \angle F'AB + \angle BAE = \angle F'AE = \angle EAF$。又 $\because AE = AE$,$\therefore \triangle AF'E \cong \triangle AFE(SAS)$,$\therefore EF = EF'$,$\therefore EF = F'E = BE + DF$。
(3) $EF = DF - BE$。解析:将 $\triangle ABE$ 绕着点 $A$ 按逆时针方向旋转 $90^{\circ}$ 得 $\triangle ADH$,$\therefore \triangle ADH \cong \triangle ABE$,$\therefore \angle DAH = \angle BAE$,$AE = AH$。$\because \angle EAF = 45^{\circ}$,$\therefore \angle BAE + \angle BAF = 45^{\circ} = \angle DAH + \angle BAF$,$\therefore \angle FAH = 90^{\circ} - \angle DAH - \angle BAF = 45^{\circ} = \angle EAF$。又 $\because AF = AF$,$AE = AH$,$\therefore \triangle AEF \cong \triangle AHF(SAS)$,$\therefore EF = FH$,$\therefore EF = FH = DF - DH = DF - BE$。
归纳总结
本题与第 9 题均属于半角模型,又称角含半角模型,即一个大角包含一个它一半大小的小角。角含半角模型中的角度,通常为特殊角,$30^{\circ}$ 和 $60^{\circ}$,$45^{\circ}$ 和 $90^{\circ}$,$60^{\circ}$ 和 $120^{\circ}$。
证明方法:①旋转法,②翻折法,③截长补短法。



(1) 如图①,将 $\triangle ADF$ 绕着点 $A$ 按顺时针方向旋转 $90^{\circ}$,得 $\triangle ABH$。
$\because$ 四边形 $ABCD$ 是正方形,$\therefore AD = AB = BC = CD$,$\angle ABC = \angle ADF = \angle C = 90^{\circ}$。$\because DF = BE = BH = 1$,由旋转可得 $AF = AH$,$\angle DAF = \angle BAH$。
$\because \angle EAF = 45^{\circ}$,$\therefore \angle DAF + \angle BAE = 45^{\circ} = \angle BAH + \angle BAE = \angle HAE = \angle EAF$。又 $\because AE = AE$,$\therefore \triangle AEF \cong \triangle AEH(SAS)$,$\therefore HE = EF = 2$。

(2) 将 $\triangle ADF$ 绕着点 $A$ 按顺时针方向旋转 $90^{\circ}$,得 $\triangle ABF'$,如图②,则 $\angle ABF' = \angle D$,$AF = AF'$,$\angle BAF' = \angle DAF$。$\because$ 四边形 $ABCD$ 是正方形,$\therefore \angle D = \angle ABC = 90^{\circ}$,$\therefore \angle ABF' = 90^{\circ}$,$\therefore \angle F'BC = 180^{\circ}$,$\therefore$ 点 $F'$,$B$,$E$ 在一条直线上。$\because \angle EAF = 45^{\circ}$,$\therefore \angle DAF + \angle BAE = 45^{\circ} = \angle F'AB + \angle BAE = \angle F'AE = \angle EAF$。又 $\because AE = AE$,$\therefore \triangle AF'E \cong \triangle AFE(SAS)$,$\therefore EF = EF'$,$\therefore EF = F'E = BE + DF$。
(3) $EF = DF - BE$。解析:将 $\triangle ABE$ 绕着点 $A$ 按逆时针方向旋转 $90^{\circ}$ 得 $\triangle ADH$,$\therefore \triangle ADH \cong \triangle ABE$,$\therefore \angle DAH = \angle BAE$,$AE = AH$。$\because \angle EAF = 45^{\circ}$,$\therefore \angle BAE + \angle BAF = 45^{\circ} = \angle DAH + \angle BAF$,$\therefore \angle FAH = 90^{\circ} - \angle DAH - \angle BAF = 45^{\circ} = \angle EAF$。又 $\because AF = AF$,$AE = AH$,$\therefore \triangle AEF \cong \triangle AHF(SAS)$,$\therefore EF = FH$,$\therefore EF = FH = DF - DH = DF - BE$。
归纳总结
本题与第 9 题均属于半角模型,又称角含半角模型,即一个大角包含一个它一半大小的小角。角含半角模型中的角度,通常为特殊角,$30^{\circ}$ 和 $60^{\circ}$,$45^{\circ}$ 和 $90^{\circ}$,$60^{\circ}$ 和 $120^{\circ}$。
证明方法:①旋转法,②翻折法,③截长补短法。




查看更多完整答案,请扫码查看


