《2025年学霸题中题八年级数学上册人教版》

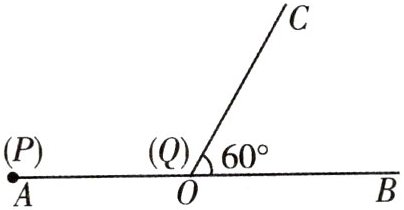
12. 如图，$\angle BOC = 60^{\circ}$，点$A$是$BO$延长线上的一点，$OA = 10\ cm$，动点$P$从点$A$出发沿$AB$以$2\ cm/s$的速度移动，动点$Q$从点$O$出发沿$OC$以$1\ cm/s$的速度移动，如果点$P$，$Q$同时出发，是否存在某一时刻$t$，使得$\triangle POQ$是等腰三角形(包含等边三角形)?

答案：
①当点P在线段OA上时，如图①所示，PO=QO，△POQ是等腰三角形。根据题意，得PO=AO−AP=(10−2t)cm，QO=tcm，
∵PO=QO，
∴10−2t=t，解得t=10/3；②当点P在射线OB上时，如图②所示，PO=QO，∠BOC=60°，△POQ是等边三角形。根据题意，得PO=AP−AO=(2t−10)cm，QO=tcm，
∴2t−10=t，解得t=10。综上，当t=10/3s或t=10s时，使得△POQ是等腰三角形。
　　　
技法点拨
本题的解题方法是解决“存在性”问题的常用方法，即先假设存在，在此基础上根据题意及相关的定理、定义、计算公式等列出关于t的方程，解方程求得t的值，如果得到的t值符合题意，那么假设成立；如果得到的t值不符合题意，那么假设不成立。

13. 在一次夏令营活动中，小明同学从营地$A$出发，要到$A$地的北偏东$60^{\circ}$方向的$C$地，他先沿正东方向走了$200\ m$到达$B$地，再沿北偏东$30^{\circ}$方向走，恰能到达目的地$C$(如图)，那么$B$，$C$两地相距______200$m$。

答案： 200　解析:
∵B地在A地的正东方向，C地在A地的北偏东60°方向，
∴∠BAC=90°−60°=30°。
∵C地在B地的北偏东30°方向，
∴∠ABC=90°+30°=120°，
∴∠C=180°−∠BAC−∠ABC=180°−30°−120°=30°，
∴∠BAC=∠C，
∴BC=AB=200m。

14. 在$\triangle ABC$中，$\angle ACB = 2\angle B$，$BC = 2AC$。求证：$\angle A = 90^{\circ}$。

答案：
如图，作∠ACB的平分线CD交AB于点D，过点D作DE⊥BC于点E。
∵∠ACB=2∠B，
∴∠B=∠BCD=1/2∠ACB，
∴BD=CD，
∴BE=CE=1/2BC。
∵BC=2AC，
∴AC=CE。
在△ACD和△ECD中，{AC=EC，∠ACD=∠ECD，CD=CD}，
∴△ACD≌△ECD(SAS)，
∴∠A=∠CED=90°。
　　　　　　　　　　　　　　　　

15. 我们知道“对称补缺”的思想是解决与轴对称图形有关的问题的一种重要的添加辅助线的策略，参考这种思想解决下列问题：
如图①，在$\triangle ABC$中，$D$为$\triangle ABC$外一点。
(1) 如图①，若$AC$平分$\angle BAD$，$CE \perp AB$于$E$，$\angle B + \angle ADC = 180^{\circ}$，求证：$BC = CD$。
(2) 如图②，在$Rt\triangle ABC$中，$AB = AC$，$\angle BAC = 90^{\circ}$，$BD$平分$\angle ABC$交$AC$于点$D$，$CE \perp BD$交$BD$的延长线于点$E$，则线段$BD$和$CE$具有什么数量关系? 证明你的结论。

(1) 在AB上取点G，使AG=AD，连接CG。∵AC平分∠BAD，∴∠DAC=∠GAC。∵AD=AG，∠DAC=∠GAC，AC=AC，∴△ADC≌△AGC(SAS)，∴DC=GC，∠CDA=∠CGA。又∵∠B+∠ADC=180°，∠CGE+∠AGC=180°，∴∠B=∠CGE。又∵CE⊥AB，∴CB=CG。∵DC=GC，∴BC=CD。
(2) 线段$BD$和$CE$的数量关系为$BD=2CE$。证明如下:延长CE与BA的延长线交于点F，∵∠BAC=90°，CE⊥BD，∴∠BAC=∠DEC。∵∠ADB=∠CDE，∴∠ABD=∠DCE。∵∠BAD=∠CAF，AB=AC，∠ABD=∠DCE，∴△BAD≌△CAF(ASA)，∴BD=CF。∵BD平分∠ABC，CE⊥DB，∴∠FBE=∠CBE。∵BE=BE，∠BEF=∠BEC，∴△BEF≌△BEC(ASA)，∴CE=EF，∴DB=CF=2CE。

答案：
(1)在AB上取点G，使AG=AD，连接CG。
∵AC平分∠BAD，
∴∠DAC=∠GAC。
∵AD=AG，∠DAC=∠GAC，AC=AC，
∴△ADC≌△AGC(SAS)，
∴DC=GC，∠CDA=∠CGA。又
∵∠B+∠ADC=180°，∠CGE+∠AGC=180°，
∴∠B=∠CGE。又
∵CE⊥AB，
∴CB=CG。
∵DC=GC，
∴BC=CD。
(2)BD=2CE。证明如下:延长CE与BA的延长线交于点F，
∵∠BAC=90°，CE⊥BD，
∴∠BAC=∠DEC。
∵∠ADB=∠CDE，
∴∠ABD=∠DCE。
∵∠BAD=∠CAF，AB=AC，∠ABD=∠DCE，
∴△BAD≌△CAF(ASA)，
∴BD=CF。
∵BD平分∠ABC，CE⊥DB，
∴∠FBE=∠CBE。
∵BE=BE，∠BEF=∠BEC，
∴△BEF≌△BEC(ASA)，
∴CE=EF，
∴DB=CF=2CE。

16. 在$\triangle ABC$中，$AB = AC$，在$\triangle ABC$的外部作等边三角形$ACD$，$E$为$AC$的中点，连接$DE$并延长交$BC$于点$F$，连接$BD$。
(1) 如图①，若$\angle BAC = 100^{\circ}$，求$\angle BDF$的度数。
(2) 如图②，$\angle ACB$的平分线交$AB$于点$M$，交$EF$于点$N$，连接$BN$。
①补全图②；
②若$BN = DN$，求证：$MB = MN$。

答案：

(1)在等边三角形ACD中，∠CAD=∠ADC=60°，AD=AC。
∵E为AC的中点，
∴∠ADE=1/2∠ADC=30°。
∵AB=AC，
∴AD=AB。
∵∠BAD=∠BAC+∠CAD=160°，
∴∠ADB=∠ABD=10°，
∴∠BDF=∠ADF−∠ADB=20°。
(2)①补全图形，如图所示。
　　　　　　　　　　
②如图，连接AN。
∵CM平分∠ACB，
∴设∠ACM=∠BCM=α。
∵AB=AC，
∴∠ABC=∠ACB=2α。在等边三角形ACD中，
∵E为AC的中点，
∴DN⊥AC，
∴NA=NC，
∴∠NAC=∠NCA=α，
∴∠DAN=60°+α。在△ABN和△ADN中，{AB=AD，BN=DN，AN=AN}，
∴△ABN≌△ADN(SSS)，
∴∠ABN=∠ADN=30°，∠BAN=∠DAN=60°+α，
∴∠BAC=60°+2α。在△ABC中，∠BAC+∠ACB+∠ABC=180°，
∴60°+2α+2α+2α=180°，
∴α=20°，
∴∠NBC=∠ABC−∠ABN=10°，
∴∠MNB=∠NBC+∠NCB=30°，
∴∠MNB=∠MBN，
∴MB=MN。