《2025年学霸题中题八年级数学上册人教版》

1. (2024·孝感月考)具备下列条件的两个三角形一定是全等三角形的是 (C)
A. 三个角对应相等
B. 两边及一边的对角对应相等
C. 两边及第三条边上的中线对应相等
D. 两边及第三条边上的高对应相等

答案： C

2. 如图,点E,F在线段BC上,$AB=DC,AE=DF,$$BF=CE$,下列结论不一定成立的是 (B)

A. $∠B=∠C$
B. $AF=FD$
C. $CF=BE$
D. $AB// DC$

答案： B

3. 如图,在$△ABC$中,已知$∠1=∠2,BE=$CD,$AB=5,AE=2$,则$CE=$3.

答案： 3

4. 如图,C是AB的中点,$AD=BE,CD=CE$,则图中全等三角形共有4对.

答案： 4

5. (2024·盘锦月考)如图,在四边形ABCD中,$AD=BC,BE=DF,AE⊥BD,CF⊥BD$,垂足分别为E,F.
(1)求证:$△ADE\cong △CBF;$
∵ $ BE = DF $，∴ $ BE - EF = DF - EF $，即 $ BF = DE $。∵ $ AE \perp BD $，$ CF \perp BD $，∴ $ \angle AED = \angle CFB = 90^\circ $。在 $ Rt\triangle ADE $ 与 $ Rt\triangle CBF $ 中，$ \left\{ \begin{array} { l } { AD = CB, } \\ { DE = BF, } \end{array} \right. $ ∴ $ Rt\triangle ADE \cong Rt\triangle CBF ( HL ) $。
(2)若AC与BD相交于点O,求证:$AO=CO.$
连接 $ AC $ 交 $ BD $ 于点 $ O $。∵ $ Rt\triangle ADE \cong Rt\triangle CBF $，∴ $ \angle ADE = \angle CBF $。在 $ \triangle AOD $ 和 $ \triangle COB $ 中，$ \left\{ \begin{array} { l } { \angle AOD = \angle COB, } \\ { \angle ADE = \angle CBF, } \\ { AD = CB, } \end{array} \right. $ ∴ $ \triangle AOD \cong \triangle COB ( AAS ) $，∴ $ AO = CO $。

答案：
(1)
∵ $ BE = DF $，
∴ $ BE - EF = DF - EF $，即 $ BF = DE $。
∵ $ AE \perp BD $，$ CF \perp BD $，
∴ $ \angle AED = \angle CFB = 90^\circ $。在 $ Rt\triangle ADE $ 与 $ Rt\triangle CBF $ 中，$ \left\{ \begin{array} { l } { AD = CB, } \\ { DE = BF, } \end{array} \right. $
∴ $ Rt\triangle ADE \cong Rt\triangle CBF ( HL ) $。
(2) 连接 $ AC $ 交 $ BD $ 于点 $ O $。
∵ $ Rt\triangle ADE \cong Rt\triangle CBF $，
∴ $ \angle ADE = \angle CBF $。在 $ \triangle AOD $ 和 $ \triangle COB $ 中，$ \left\{ \begin{array} { l } { \angle AOD = \angle COB, } \\ { \angle ADE = \angle CBF, } \\ { AD = CB, } \end{array} \right. $
∴ $ \triangle AOD \cong \triangle COB ( AAS ) $，
∴ $ AO = CO $。

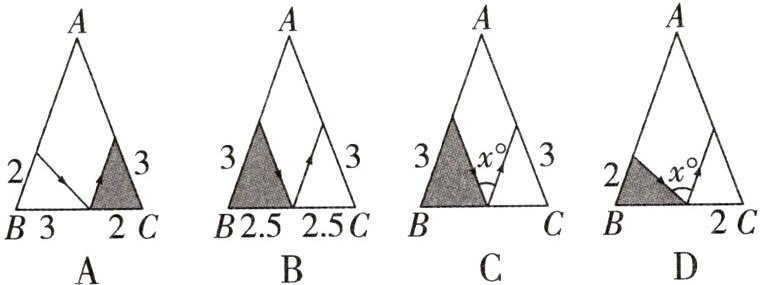
6. 如图,有一张三角形纸片ABC,已知$∠B=$$∠C=x^{\circ }$,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是 ( )

答案：
C 解析：对于C，如图，
∵ $ \angle DEC = \angle B + \angle BDE $，
∴ $ x ^ { \circ } + \angle FEC = x ^ { \circ } + \angle BDE $，
∴ $ \angle FEC = \angle BDE $，

∴其对应边应该是BE和CF，而已知给的是BD = FC = 3，
∴不能判定两个小三角形全等。

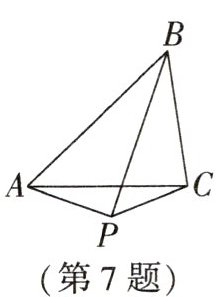
7. 如图,已知$△ABC$的面积为8,BP为$∠ABC$的平分线,$AP⊥BP$于点P,则$△BCP$的面积为 (C)

A. 3.5
B. 3.9
C. 4
D. 4.2

答案： C 解析：延长 $ AP $ 交 $ BC $ 的延长线于点 $ E $，由题意，得 $ \angle APB = \angle BPE = 90 ^ { \circ } $，$ \angle ABP = \angle EBP $。由题易得 $ \triangle ABP \cong \triangle EBP $，
∴ $ S _ { \triangle ABP } = S _ { \triangle BEP } $，$ AP = PE $，
∴ $ \triangle APC $ 和 $ \triangle CPE $ 等底等高，
∴ $ S _ { \triangle APC } = S _ { \triangle PCE } $。设 $ \triangle ACE $ 的面积为 $ m $，
∴ $ S _ { \triangle ABE } = S _ { \triangle ABC } + S _ { \triangle ACE } = 8 + m $，
∴ $ S _ { \triangle PBC } = \frac { 1 } { 2 } S _ { \triangle ABE } - \frac { 1 } { 2 } S _ { \triangle ACE } = 4 $。

8. (2024·宁波期末)如图,在$△ABC$中,$AB=AC,$P,Q分别为边AB,AC上两个动点,在运动过程中始终保持$AP+AQ=AB$,连接BQ和CP,当$BQ+CP$值达到最小时,$\frac {AP}{AQ}$的值为____.

答案：
1 解析：如图，过点 $ B $ 作 $ BE // AC $，且 $ BE = AC $，在 $ BA $ 上截取 $ BH = AP $，连接 $ CH $，$ EH $。
∵ $ AB = AC $，$ AP + AQ = AB $，$ AB = AP + BP $，$ AC = AQ + CQ $，
∴ $ AQ = BP $，$ CQ = AP = BH $。
∵ $ AC // BE $，
∴ $ \angle A = \angle EBH $。在 $ \triangle ACP $ 和 $ \triangle BEH $ 中，$ \left\{ \begin{array} { l } { AC = BE, } \\ { \angle A = \angle EBH, } \\ { AP = BH, } \end{array} \right. $

∴ $ \triangle ACP \cong \triangle BEH ( SAS ) $，
∴ $ AC = BE $，$ CP = HE $。
∵ $ AB = AC $，
∴ $ \angle ACB = \angle ABC $。在 $ \triangle CBQ $ 和 $ \triangle BCH $ 中，$ \left\{ \begin{array} { l } { CB = BC, } \\ { \angle BCQ = \angle CBH, } \\ { CQ = BH, } \end{array} \right. $
∴ $ \triangle CBQ \cong \triangle BCH ( SAS ) $，
∴ $ CH = BQ $，
∴ $ BQ + CP = CH + HE $，
∴ 当 $ C $，$ E $，$ H $ 三点共线时，$ BQ + CP $ 有最小值。
∵ $ AC // BE $，
∴ $ \angle ACH = \angle BEH $。又
∵ $ AC = BE $，$ \angle A = \angle EBA $，
∴ $ \triangle ACH \cong \triangle BEH ( ASA ) $，
∴ $ AH = BH $，
∴ 点 $ H $ 是 $ AB $ 的中点，
∴ $ AP = BH = \frac { 1 } { 2 } AB $，
∴ 点 $ P $ 与点 $ H $ 重合，
∴ $ BP = BH = AQ = AP $，
∴ $ \frac { AP } { AQ } = 1 $。

9. (2024·汕头期中)如图,在$△ABC$中,以AB,AC为腰作等腰直角三角形ABE和等腰直角三角形ACF,连接EF,AD为BC边上的高线,延长DA交EF于点N,下列结论:①$∠EAN=∠ABC$;②$△EAN\cong △BAD$;③$S_{△AEF}=S_{△ABC}$;④$EN=FN$.其中正确的有____.(写上序号)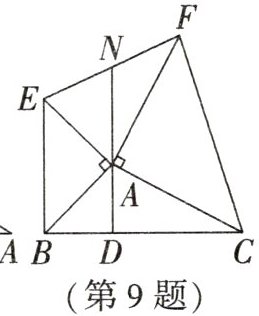

答案：
①③④ 解析：
∵ $ \angle BAE = 90 ^ { \circ } $，$ AD \perp BD $，
∴ $ \angle EAN + \angle BAD = 90 ^ { \circ } = \angle ABC + \angle BAD $，
∴ $ \angle EAN = \angle ABC $，故①正确；
∵ $ \angle AEN $ 与 $ \angle BAD $ 不一定相等，
∴ $ \triangle AEN $ 与 $ \triangle BAD $ 不一定全等，故②错误；如图，作 $ EH \perp AN $，交 $ AN $ 于点 $ H $，作 $ FK \perp AN $，交 $ AN $ 的延长线于点 $ K $，
∴ $ \angle AEH + \angle EAH = 90 ^ { \circ } $。
∵ $ \angle EAB = 90 ^ { \circ } $，
∴ $ \angle EAH + \angle BAD = 90 ^ { \circ } $，
∴ $ \angle AEH = \angle BAD $。在 $ \triangle AEH $ 和 $ \triangle BAD $ 中，$ \left\{ \begin{array} { l } { \angle AHE = \angle BDA, } \\ { \angle AEH = \angle BAD, } \\ { AE = AB, } \end{array} \right. $

∴ $ \triangle AEH \cong \triangle BAD ( AAS ) $，
∴ $ EH = AD $，$ S _ { \triangle ABD } = S _ { \triangle EAH } $。同理可得 $ \triangle AFK \cong \triangle CAD $，
∴ $ FK = AD $，$ S _ { \triangle FKA } = S _ { \triangle ADC } $，
∴ $ FK = EH $。在 $ \triangle FKN $ 和 $ \triangle EHN $ 中，$ \left\{ \begin{array} { l } { \angle FKN = \angle EHN, } \\ { \angle FNK = \angle ENH, } \\ { FK = EH, } \end{array} \right. $
∴ $ \triangle FKN \cong \triangle EHN ( AAS ) $，
∴ $ S _ { \triangle ENH } = S _ { \triangle FNK } $，
∴ $ S _ { \triangle ABC } = S _ { \triangle ABD } + S _ { \triangle ADC } = S _ { \triangle AEH } + S _ { \triangle AFK } = ( S _ { \triangle EAN } - S _ { \triangle ENH } ) + ( S _ { \triangle FNA } + S _ { \triangle FNK } ) = S _ { \triangle EAN } + S _ { \triangle FNA } = S _ { \triangle AEF } $，即 $ S _ { \triangle ABC } = S _ { \triangle AEF } $，故③正确；
∵ $ \triangle FKN \cong \triangle EHN $，
∴ $ FN = EN $，故④正确。故答案为①③④。