《2025年学霸题中题八年级数学上册人教版》

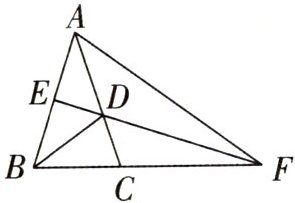
11. 如图,在$\triangle ABC$中,$AB=AC,∠BAC=36^{\circ },BD$是$∠ABC$的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.下列结论:①$EF⊥AB$;②$\triangle ADB$为等腰三角形;③$DB=DF$;④$\triangle ACF$为等腰三角形.其中错误的有 (A)

A. 1个
B. 2个
C. 3个
D. 4个

答案： A　解析:
∵AB=AC,∠BAC=36°,
∴∠ABC=72°.又
∵BD是∠ABC 的平分线，
∴∠ABD=36°,
∴∠BAD=∠ABD,
∴AD=BD,即△ADB 是等腰三角形,故②正确;又
∵E是AB的中点,
∴DE⊥AB,即FE⊥AB,故①正确;
∵FE⊥AB,AE=BE,
∴FE垂直平分AB,
∴AF=BF,
∴∠BAF=∠ABF.又
∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°.又
∵∠ACB=72°,
∴∠AFC=∠ACB−∠CAF=36°,
∴∠CAF=∠AFC=36°,
∴AC=CF,即△ACF为等腰三角形,故④正确

12. (1)在平面直角坐标系中,已知两点$A(1,2),B(-1,-1)$,若$\triangle ABC$是以线段AB为一腰,对称轴平行于y轴的等腰三角形,则C点的坐标是(3,−1)或(−3,2).
(2)在平面直角坐标系xOy中,已知点$A(2,-2)$,在y轴上确定点P,使$\triangle AOP$为等腰三角形,则符合条件的点P的个数为4.

答案：
(1)(3,−1)或(−3,2)　解析:分两种情况:①当A为顶角顶点时，根据题意，得等腰三角形的对称轴为直线x=1,
∵点B的坐标为(−1,−1),
∴点C的坐标为(3,−1);②当B为顶角顶点时,根据题意,得等腰三角形的对称轴为直线x=−1,
∵点A的坐标为(1,2),
∴点C的坐标为(−3,2).综上所述,点C的坐标为(3,−1)或(−3,2).
(2)4　解析:分情况进行讨论:当OA为等腰三角形的腰时,以O 为圆心,OA的长为半径的圆弧与y轴有两个交点，以A为圆心,AO 的长为半径的圆弧与y轴有一个交点(原点除外);当OA为等腰三角形的底时，作线段OA的垂直平分线，与y轴有一个交点.
∴符合条件的点一共有4个

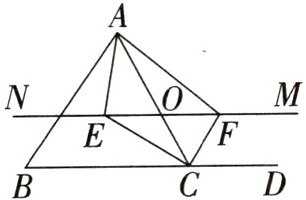
13. (2024·上海月考)如图,$\triangle ABC$中,点O是AC边上的一个动点,过点O作直线$MN// BC$,直线MN交$∠BCA$的平分线于点E,交$∠BCA$的邻补角的平分线于点F,设OC的长为x,EF的长为y.那么y与x的数量关系是______y=2x.

答案： y=2x　解析:
∵MN//BC,
∴∠OEC=∠BCE,∠OFC=∠DCF;又
∵CE平分∠BCO,CF平分∠ACD,
∴∠OCE=∠BCE,∠OCF=∠DCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EF=2CO.
∵OC的长为x,EF的长为y,
∴y=2x.

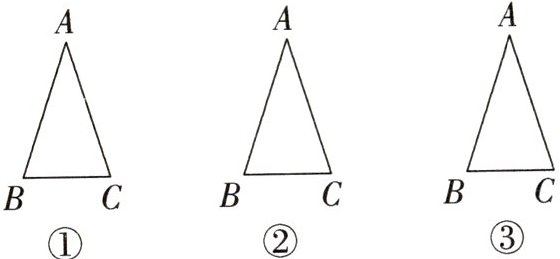
14. 如图,$\triangle ABC$中,$AB=AC,∠A=36^{\circ }$,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括$\triangle ABC$)
(1)在图①中画1条线段,使图中有2个等腰三角形,并直接写出这两个等腰三角形的顶角度数分别是______°和______°;
(2)在图②中画2条线段,使图中有4个等腰三角形;
(3)继续按以上操作发现:在$\triangle ABC$中画n条线段,则图中有______个等腰三角形,其中有______个黄金等腰三角形.(用含n的式子表示)

答案：

(1)画图如图①所示.(答案不唯一)　108　36
解析:如图①所示,
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∴当AE=BE时,∠A=∠ABE=36°,
∴∠AEB=108°,
∴∠EBC=∠ABC−∠ABE=36°,
∴这两个等腰三角形的顶角度数分别是108°和36°.



(2)如图②所示.(答案不唯一)
(3)2n　n　解析:如图③所示,当画1条线段时,可得到2个等腰三角形;当画2条线段时,可得到4个等腰三角形;当画3条线段时，可得到6个等腰三角形……在△ABC中画n条线段,则图中有2n个等腰三角形，其中有n个黄金等腰三角形.

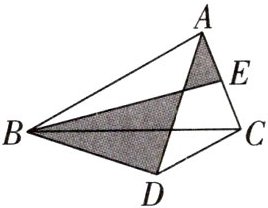
15. 如图,$\triangle ABC$中,$AC=DC=3$,BD垂直于$∠BAC$的平分线于D,E为AC的中点,则图中两个阴影部分面积之差的最大值为 (C)

A. 1.5
B. 3
C. 4.5
D. 9

答案： C　解析:延长BD交AC的延长线于点H.设AD交BE于点O.
∵AD⊥BH,
∴∠ADB=∠ADH=90°,
∴∠ABD+∠BAD=90°,∠H+∠HAD=90°.
∵∠BAD=∠HAD,∠ABD=∠H,AB=AH.
∵AD⊥BH,
∴BD=DH.
∵DC=CA,
∴∠CDA=∠CAD.
∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,
∴∠CDH=∠H,
∴CD=CH=AC.
∵AE=EC,
∴S△ABE=1/4S△ABH,S△CDH=1/4S△ABH,
∴S△ABE=S△CDH,
∴S△OBD−S△AOE=S△ADB−S△ABE=S△ADH−S△CDH=S△ACD.
∵AC=CD=3,
∴当DC⊥AC时,△ACD的面积最大,最大面积为1/2×3×3=4.5.

16. (2024·无锡期中)在$\triangle ABC$中,$AB=AC,∠BAC=100^{\circ }$,点D在BC边上,$\triangle ABD$和$\triangle AFD$关于直线AD对称,$∠FAC$的平分线交BC于点G,连接FG.
(1)求$∠DFG$的度数.80°
(2)设$∠BAD=m^{\circ }$.
①当$\triangle DFG$为等腰三角形时,请求出此时m的值.10、25或40
②$\triangle DFG$有可能是直角三角形吗? 若有,请直接写出相应m的值;若没有,请说明理由.5或45

答案：
(1)
∵AB=AC,∠BAC=100°,
∴∠B=∠C=40°.
∵△ABD和△AFD 关于直线AD对称，
∴△ADB≌△ADF,
∴∠B=∠AFD=40°,AB=AF,∠BAD=∠FAD,
∴AF=AC.
∵AG平分∠FAC,
∴∠FAG=∠CAG.在△AGF和△AGC中,{AF=AC,∠FAG=∠CAG,AG=AG},
∴△AGF≌△AGC (SAS),
∴∠AFG=∠C;
∵∠DFG=∠AFD+∠AFG,
∴∠DFG=∠B+∠C=40°+40°=80°.
(2)①当GD=GF时,∠GDF=∠GFD=80°.
∵∠ADG=40°+m°,
∴在△ADF中,40 + 80 + 40 + m + m = 180,
∴m = 10.当DF=GF时,∠FDG=∠FGD.
∵∠DFG=80°,
∴∠FDG=∠FGD=50°.
∴在△ADF中,40 + 50 + 40 + 2m = 180,
∴m = 25.当DF=DG时,∠DFG=∠DGF=80°,
∴∠GDF=20°,
∴在△ADF中,40 + 20 + 40 + 2m = 180,
∴m = 40.
∴当m = 10、25或40时，△DFG为等腰三角形.
②△DFG有可能是直角三角形,m = 5或45. 解析:当∠GDF=90°时,
∵∠DFG=80°,
∴在△ADF中,40 + 90 + 40 + 2m = 180,
∴m = 5;当∠DGF=90°时,
∵∠DFG=80°,
∴∠GDF=10°,
∴在△ADF中,40 + 10 + 40 + 2m = 180,
∴m = 45.综上所述,当m = 5或45时,△DFG为直角三角形