第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
1.(2024·重庆中考)下列四种化学仪器的示意图中,是轴对称图形的是(

C
)
答案:
C
2.(2024·西藏中考)如图,已知直线$l_{1}// l_{2}$,$AB\perp CD$于点$D$,$\angle 1 = 50^{\circ}$,则$\angle 2$的度数是(
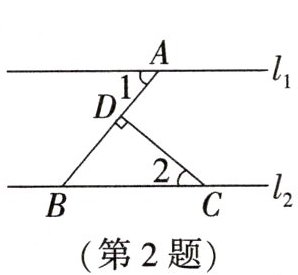
A. $40^{\circ}$
B. $45^{\circ}$
C. $50^{\circ}$
D. $60^{\circ}$
A
)
A. $40^{\circ}$
B. $45^{\circ}$
C. $50^{\circ}$
D. $60^{\circ}$
答案:
A
3. 如图,在$\triangle ABC$中,$\angle A = 50^{\circ}$,$\angle ABC = 70^{\circ}$,$BD$平分$\angle ABC$,则$\angle BDC$的度数是(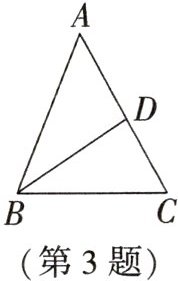
A. $85^{\circ}$
B. $80^{\circ}$
C. $75^{\circ}$
D. $70^{\circ}$
A
)
A. $85^{\circ}$
B. $80^{\circ}$
C. $75^{\circ}$
D. $70^{\circ}$
答案:
A
4. 如图,四边形$AMBN$是轴对称图形,直线$MN$是四边形$AMBN$的对称轴,与对角线$AB$交于点$Q$,点$P$是直线$MN$上一点,下列判断错误的是(

A. $AQ = BQ$
B. $AP = BP$
C. $\angle MAP = \angle MBP$
D. $\angle ANM = \angle NMB$
D
)
A. $AQ = BQ$
B. $AP = BP$
C. $\angle MAP = \angle MBP$
D. $\angle ANM = \angle NMB$
答案:
D
5. 如图,$AE// DF$,$AE = DF$.下列条件:①$AB = CD$;②$CE// BF$;③$CE = BF$;④$\angle E = \angle F$.其中能使$\triangle EAC\cong \triangle FDB$的有(
A. 1个
B. 2个
C. 3个
D. 4个
C
)
A. 1个
B. 2个
C. 3个
D. 4个
答案:
C
6. 把一根长$50\mathrm{cm}$的铁丝围成一个等腰三角形,使其中一边的长比另一边的2倍少$5\mathrm{cm}$,则该三角形的边长不可能为(
A. $12\mathrm{cm}$
B. $19\mathrm{cm}$
C. $22.5\mathrm{cm}$
D. $13\mathrm{cm}$
D
)A. $12\mathrm{cm}$
B. $19\mathrm{cm}$
C. $22.5\mathrm{cm}$
D. $13\mathrm{cm}$
答案:
D
7.(2024·枣庄期末)如图,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AD$是高,$BE$是中线,$CF$是角平分线,$CF$交$AD$于点$G$,交$BE$于点$H$,下列说法错误的是(

A. $S_{\triangle ABE} = S_{\triangle BCE}$
B. $\angle AFG = \angle AGF$
C. $\angle FAG = 2\angle ACF$
D. $BH = CH$
D
)
A. $S_{\triangle ABE} = S_{\triangle BCE}$
B. $\angle AFG = \angle AGF$
C. $\angle FAG = 2\angle ACF$
D. $BH = CH$
答案:
D 解析:
∵BE是中线,
∴AE=CE,
∴$S_{△ABE}=S_{△BCE}$ (等底同高),故A正确。
∵CF是角平分线,
∴$∠ACF = ∠BCF$。
∵AD为高,
∴$∠ADC = 90°$,$∠ACB + ∠CAD = 90°$。
∵$∠BAC = 90°$,
∴$∠ABC + ∠ACB = 90°$,
∴$∠ABC = ∠CAD$。
∵$∠AFG = ∠ABC + ∠BCF$,$∠AGF = ∠CAD + ∠ACF$,
∴$∠AFG = ∠AGF$,故B正确。
∵$∠ABC + ∠ACB = 90°$,$∠ABC + ∠BAD = 90°$,
∴$∠ACB = ∠BAD$。
∵CF是$∠ACB$的平分线,
∴$∠ACB = 2∠ACF$,
∴$∠BAD = 2∠ACF$,即$∠FAG = 2∠ACF$,故C正确。根据已知条件不能推出$∠HBC = ∠HCB$,即不能推出BH = CH,故D错误。
∵BE是中线,
∴AE=CE,
∴$S_{△ABE}=S_{△BCE}$ (等底同高),故A正确。
∵CF是角平分线,
∴$∠ACF = ∠BCF$。
∵AD为高,
∴$∠ADC = 90°$,$∠ACB + ∠CAD = 90°$。
∵$∠BAC = 90°$,
∴$∠ABC + ∠ACB = 90°$,
∴$∠ABC = ∠CAD$。
∵$∠AFG = ∠ABC + ∠BCF$,$∠AGF = ∠CAD + ∠ACF$,
∴$∠AFG = ∠AGF$,故B正确。
∵$∠ABC + ∠ACB = 90°$,$∠ABC + ∠BAD = 90°$,
∴$∠ACB = ∠BAD$。
∵CF是$∠ACB$的平分线,
∴$∠ACB = 2∠ACF$,
∴$∠BAD = 2∠ACF$,即$∠FAG = 2∠ACF$,故C正确。根据已知条件不能推出$∠HBC = ∠HCB$,即不能推出BH = CH,故D错误。
8. 如图,$\triangle ABC$的面积等于6,边$AC = 3$.现将$\triangle ABC$沿$AB$所在直线翻折,使点$C$落在直线$AD$上的$C'$处,$P$为直线$AD$上的一点,则线段$BP$的长不可能是( )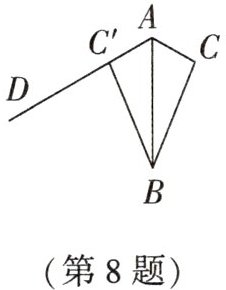
A. 3
B. 4
C. 5.5
D. 6

A. 3
B. 4
C. 5.5
D. 6
答案:
A 解析:如图,过点B作$BE⊥AC$交AC的延长线于点E,过点B作$BE'⊥AD$于点$E'$。由翻折可知AB平分$∠DAC$,则$BE = BE'$。在$△ABC$中,
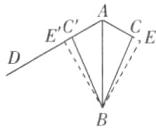
∵$\frac{1}{2}AC·BE = 6$,
∴$BE = \frac{6×2}{3} = 4$,
∴$BE' = BE = 4$。
∵点P在直线AD上,
∴由垂线段最短可知$BP≥BE' = 4$,则线段BP的长不可能是3,故选A。
A 解析:如图,过点B作$BE⊥AC$交AC的延长线于点E,过点B作$BE'⊥AD$于点$E'$。由翻折可知AB平分$∠DAC$,则$BE = BE'$。在$△ABC$中,

∵$\frac{1}{2}AC·BE = 6$,
∴$BE = \frac{6×2}{3} = 4$,
∴$BE' = BE = 4$。
∵点P在直线AD上,
∴由垂线段最短可知$BP≥BE' = 4$,则线段BP的长不可能是3,故选A。
9.(2025·娄底期末)如图,在$\triangle ABC$中,$\angle ABC = 52^{\circ}$,$P$为$\triangle ABC$内一点,过点$P$的直线$MN$分别交$AB$,$BC$于点$M$,$N$,若$M$在$PA$的垂直平分线上,$N$在$PC$的垂直平分线上,则$\angle APC$的度数为(

A. $104^{\circ}$
B. $116^{\circ}$
C. $128^{\circ}$
D. $142^{\circ}$
B
)
A. $104^{\circ}$
B. $116^{\circ}$
C. $128^{\circ}$
D. $142^{\circ}$
答案:
B 解析:
∵$∠ABC = 52°$,
∴$∠BMN + ∠BNM = 180° - ∠ABC = 180° - 52° = 128°$。
∵M在PA的垂直平分线上,N在PC的垂直平分线上,
∴MA = MP,NP = NC,
∴$∠MAP = ∠MPA$,$∠NPC = ∠NCP$。
∵$∠BMN = ∠MAP + ∠MPA = 2∠MPA$,$∠BNM = ∠NCP + ∠NPC = 2∠NPC$,
∴$∠MPA + ∠NPC = \frac{1}{2}∠BMN + \frac{1}{2}∠BNM = \frac{1}{2}×128° = 64°$,
∴$∠APC = 180° - (∠MPA + ∠NPC) = 180° - 64° = 116°$。
∵$∠ABC = 52°$,
∴$∠BMN + ∠BNM = 180° - ∠ABC = 180° - 52° = 128°$。
∵M在PA的垂直平分线上,N在PC的垂直平分线上,
∴MA = MP,NP = NC,
∴$∠MAP = ∠MPA$,$∠NPC = ∠NCP$。
∵$∠BMN = ∠MAP + ∠MPA = 2∠MPA$,$∠BNM = ∠NCP + ∠NPC = 2∠NPC$,
∴$∠MPA + ∠NPC = \frac{1}{2}∠BMN + \frac{1}{2}∠BNM = \frac{1}{2}×128° = 64°$,
∴$∠APC = 180° - (∠MPA + ∠NPC) = 180° - 64° = 116°$。
10.(宁德中考)如图,已知等边$\triangle ABC$,$AB = 2$,点$D$在$AB$上,点$F$在$AC$的延长线上,$BD = CF$,$DE\perp BC$于$E$,$FG\perp BC$的延长线于$G$,$DF$交$BC$于点$P$,则下列结论:①$BE = CG$;②$\triangle EDP\cong \triangle GFP$;③$\angle EDP = 60^{\circ}$;④$EP = 1$,其中一定正确的有(
A. 1个
B. 2个
C. 3个
D. 4个
C
)A. 1个
B. 2个
C. 3个
D. 4个
答案:
C 解析:
∵$△ABC$是等边三角形,
∴AB = BC = AC,$∠A = ∠B = ∠ACB = 60°$,
∴$∠GCF = ∠ACB = 60°$。
∵$DE⊥BC$,$FG⊥BC$,
∴$∠DEB = ∠FGC = ∠DEP = 90°$。在$△DEB$和$△FGC$中,$\begin{cases} ∠DEB = ∠FGC \\ ∠B = ∠GCF \\ BD = CF \end{cases}$,
∴$△DEB≌△FGC(AAS)$,
∴BE = CG,DE = FG,故①正确;在$△DEP$和$△FGP$中,$\begin{cases} ∠DEP = ∠FGP \\ ∠DPE = ∠FPG \\ DE = FG \end{cases}$,
∴$△DEP≌△FGP(AAS)$,故②正确;
∵无法证明$∠EDP = 60°$,故③错误;
∵PG = PC + CG,
∴PE = PC + BE。
∵BC = PE + PC + BE = 2,
∴PE = 1,故④正确。综上,正确的有①②④,故选C。
∵$△ABC$是等边三角形,
∴AB = BC = AC,$∠A = ∠B = ∠ACB = 60°$,
∴$∠GCF = ∠ACB = 60°$。
∵$DE⊥BC$,$FG⊥BC$,
∴$∠DEB = ∠FGC = ∠DEP = 90°$。在$△DEB$和$△FGC$中,$\begin{cases} ∠DEB = ∠FGC \\ ∠B = ∠GCF \\ BD = CF \end{cases}$,
∴$△DEB≌△FGC(AAS)$,
∴BE = CG,DE = FG,故①正确;在$△DEP$和$△FGP$中,$\begin{cases} ∠DEP = ∠FGP \\ ∠DPE = ∠FPG \\ DE = FG \end{cases}$,
∴$△DEP≌△FGP(AAS)$,故②正确;
∵无法证明$∠EDP = 60°$,故③错误;
∵PG = PC + CG,
∴PE = PC + BE。
∵BC = PE + PC + BE = 2,
∴PE = 1,故④正确。综上,正确的有①②④,故选C。
查看更多完整答案,请扫码查看


