第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
3. (2025·盘锦期末)综合与实践
问题情境:数学课上,老师让每个组准备了一张如图①所示的等腰三角形纸片 $ \triangle ABC $,其中 $ AB = AC $,AD 是边 BC 上的中线.老师要求各个小组结合所学的图形变化的知识展开数学探究.
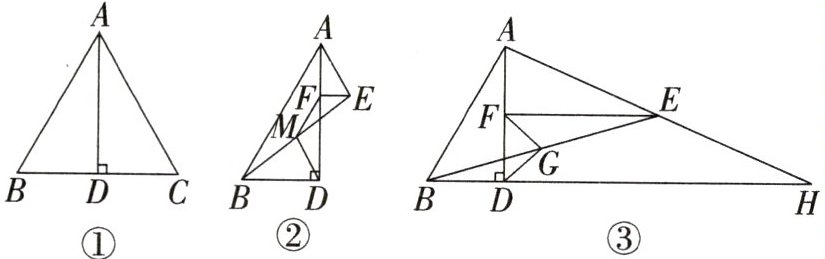
(1)如图①,“勤学”小组发现图中的 $ AD \perp BC $,请你用全等三角形的知识证明这一结论.
(2)如图②,“善思”小组将图①中的 $ \triangle ABC $ 纸片过点 E 沿平行于 BC 的直线减掉一部分,连接 BE,并在 BE 上取一点 M,连接 MD,MF,使得 $ MD = MF $.求证:$ MB = ME $.
(3)如图③,“智慧”小组将 $ \triangle ABC $ 纸片沿 AD 剪开,然后保持 $ \triangle ABD $ 不动,调整 $ \triangle ACD $ 的位置至 $ \triangle EAF $,延长 AE,BD 交于点 H,连接 BE,取 BE 的中点 G,连接 GD,GF.求证:$ GD \perp GF $.
问题情境:数学课上,老师让每个组准备了一张如图①所示的等腰三角形纸片 $ \triangle ABC $,其中 $ AB = AC $,AD 是边 BC 上的中线.老师要求各个小组结合所学的图形变化的知识展开数学探究.

(1)如图①,“勤学”小组发现图中的 $ AD \perp BC $,请你用全等三角形的知识证明这一结论.
(2)如图②,“善思”小组将图①中的 $ \triangle ABC $ 纸片过点 E 沿平行于 BC 的直线减掉一部分,连接 BE,并在 BE 上取一点 M,连接 MD,MF,使得 $ MD = MF $.求证:$ MB = ME $.
(3)如图③,“智慧”小组将 $ \triangle ABC $ 纸片沿 AD 剪开,然后保持 $ \triangle ABD $ 不动,调整 $ \triangle ACD $ 的位置至 $ \triangle EAF $,延长 AE,BD 交于点 H,连接 BE,取 BE 的中点 G,连接 GD,GF.求证:$ GD \perp GF $.
答案:
(1)$\because AD$是边$BC$上的中线,$\therefore BD = CD$,
在$\triangle ABD$和$\triangle ACD$中,$\begin{cases} AB = AC, \\ AD = AD, \\ BD = CD, \end{cases}$ $\therefore \triangle ABD \cong \triangle ACD(SSS)$,
$\therefore \angle ADB = \angle ADC = 90^{\circ}$,$\therefore AD \perp BC$。
(2)延长$FM$交$BD$于点$G$,如图①,
$\because MD = MF$,$\therefore \angle MFD = \angle MDF$,由
(1)知$\angle ADB = 90^{\circ}$,$\therefore \angle MDG + \angle MDF = 90^{\circ}$,$\angle MGD + \angle MFD = 90^{\circ}$,$\therefore \angle MDG = \angle MGD$,$\therefore MG = MD = FM$。由题意得$EF // BD$,$\therefore \angle MBG = \angle FEM$,$\angle MGB = \angle MFE$,$\therefore \triangle BGM \cong \triangle EFM(AAS)$,$\therefore BM = EM$。

(3)延长$DG$交$EF$于点$K$,如图②,
由题意得$EF // BD$,$\therefore \angle DBG = \angle KEG$,$\angle BDG = \angle EKG$。
又$\because BG = EG$,$\therefore \triangle BGD \cong \triangle EKG(AAS)$,
$\therefore KE = BD$,$KG = DG$。由题意可知$\triangle EAF \cong \triangle ACD$,由
(1)可知$\triangle ABD \cong \triangle ACD$,$\therefore \triangle EAF \cong \triangle ABD$,$\therefore AF = BD$,$AD = EF$。$\because DF = AD - AF$,$KF = EF - KE$,$\therefore FD = FK$。
又$\because FG = FG$,$\therefore \triangle DFG \cong \triangle KFG(SSS)$,$\therefore \angle FGD = \angle FGK = 90^{\circ}$,$\therefore GD \perp GF$。
(1)$\because AD$是边$BC$上的中线,$\therefore BD = CD$,
在$\triangle ABD$和$\triangle ACD$中,$\begin{cases} AB = AC, \\ AD = AD, \\ BD = CD, \end{cases}$ $\therefore \triangle ABD \cong \triangle ACD(SSS)$,
$\therefore \angle ADB = \angle ADC = 90^{\circ}$,$\therefore AD \perp BC$。
(2)延长$FM$交$BD$于点$G$,如图①,
$\because MD = MF$,$\therefore \angle MFD = \angle MDF$,由
(1)知$\angle ADB = 90^{\circ}$,$\therefore \angle MDG + \angle MDF = 90^{\circ}$,$\angle MGD + \angle MFD = 90^{\circ}$,$\therefore \angle MDG = \angle MGD$,$\therefore MG = MD = FM$。由题意得$EF // BD$,$\therefore \angle MBG = \angle FEM$,$\angle MGB = \angle MFE$,$\therefore \triangle BGM \cong \triangle EFM(AAS)$,$\therefore BM = EM$。

(3)延长$DG$交$EF$于点$K$,如图②,
由题意得$EF // BD$,$\therefore \angle DBG = \angle KEG$,$\angle BDG = \angle EKG$。
又$\because BG = EG$,$\therefore \triangle BGD \cong \triangle EKG(AAS)$,
$\therefore KE = BD$,$KG = DG$。由题意可知$\triangle EAF \cong \triangle ACD$,由
(1)可知$\triangle ABD \cong \triangle ACD$,$\therefore \triangle EAF \cong \triangle ABD$,$\therefore AF = BD$,$AD = EF$。$\because DF = AD - AF$,$KF = EF - KE$,$\therefore FD = FK$。
又$\because FG = FG$,$\therefore \triangle DFG \cong \triangle KFG(SSS)$,$\therefore \angle FGD = \angle FGK = 90^{\circ}$,$\therefore GD \perp GF$。
4. (2025·茂名期末)综合探究:
问题情境:在数学活动课上,老师提出了一个问题:如图①,在 $ \triangle ABC $ 中,BD 平分 $ \angle ABC $,$ AD \perp BD $ 于点 D,过点 D 作 $ EF // BC $ 分别交 AB,AC 于点 E,F.
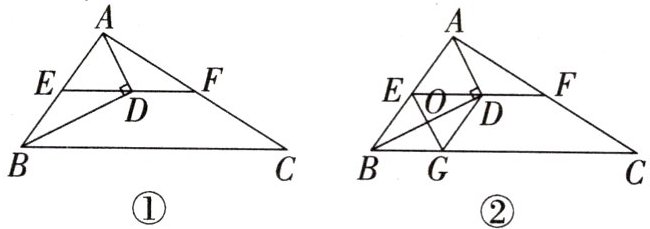
(1)问题解决:如图①,若 $ \angle BAC : \angle ABC : \angle ACB = 3 : 2 : 1 $,求 $ \angle DAC $ 的度数.
(2)如图①,若 $ \angle BED = 128^{\circ}, \angle DAF = \frac{1}{2} \angle BAD $,试猜想 $ \angle DAF $ 与 $ \angle C $ 之间的数量关系,并说明理由.
(3)问题拓展:如图②,若过点 D 作 $ DG // AB $ 交 BC 于点 G,连接 EG,交 BD 于点 O,试探究 BD 与 EG 的位置关系,并说明理由.
(1)
(2)$\angle DAF$与$\angle C$之间的数量关系为
(3)BD 与 EG 的位置关系为
问题情境:在数学活动课上,老师提出了一个问题:如图①,在 $ \triangle ABC $ 中,BD 平分 $ \angle ABC $,$ AD \perp BD $ 于点 D,过点 D 作 $ EF // BC $ 分别交 AB,AC 于点 E,F.

(1)问题解决:如图①,若 $ \angle BAC : \angle ABC : \angle ACB = 3 : 2 : 1 $,求 $ \angle DAC $ 的度数.
(2)如图①,若 $ \angle BED = 128^{\circ}, \angle DAF = \frac{1}{2} \angle BAD $,试猜想 $ \angle DAF $ 与 $ \angle C $ 之间的数量关系,并说明理由.
(3)问题拓展:如图②,若过点 D 作 $ DG // AB $ 交 BC 于点 G,连接 EG,交 BD 于点 O,试探究 BD 与 EG 的位置关系,并说明理由.
(1)
30°
(2)$\angle DAF$与$\angle C$之间的数量关系为
$\angle DAF = \angle C$
(3)BD 与 EG 的位置关系为
$BD \perp EG$
答案:
(1)设$\angle ACB = x$,则$\angle ABC = 2x$,$\angle BAC = 3x$,$\because \angle ACB + \angle ABC + \angle BAC = 180^{\circ}$,$\therefore x + 2x + 3x = 180^{\circ}$,$\therefore x = 30^{\circ}$,$\therefore \angle ABC = 2x = 60^{\circ}$,$\angle BAC = 3x = 90^{\circ}$,$\because BD$平分$\angle ABC$,$\therefore \angle ABD = 30^{\circ}$,$\because AD \perp BD$,$\therefore \angle BAD = 90^{\circ} - 30^{\circ} = 60^{\circ}$,$\therefore \angle DAC = \angle BAC - \angle BAD = 90^{\circ} - 60^{\circ} = 30^{\circ}$。
(2)$\angle DAF = \angle C$。
理由:$\because EF // BC$,$\angle BED = 128^{\circ}$,$\therefore \angle ABC = 180^{\circ} - \angle BED = 180^{\circ} - 128^{\circ} = 52^{\circ}$,$\because BD$平分$\angle ABC$,$\therefore \angle ABD = \frac{1}{2} \angle ABC = \frac{1}{2} \times 52^{\circ} = 26^{\circ}$。
$\because AD \perp BD$,$\therefore \angle BAD = 90^{\circ} - 26^{\circ} = 64^{\circ}$,$\because \angle DAF = \frac{1}{2} \angle BAD = \frac{1}{2} \times 64^{\circ} = 32^{\circ}$,$\therefore \angle BAC = \angle BAD + \angle DAF = 64^{\circ} + 32^{\circ} = 96^{\circ}$,$\therefore \angle C = 180^{\circ} - \angle BAC - \angle ABC = 180^{\circ} - 96^{\circ} - 52^{\circ} = 32^{\circ}$,$\therefore \angle DAF = \angle C$。
(3)$BD \perp EG$。理由:$\because EF // BC$,$\therefore \angle EDB = \angle DBC$,$\because BD$平分$\angle ABC$,$\therefore \angle EBD = \angle DBG$,$\therefore \angle EBD = \angle EDB$,$\therefore BE = ED$。
$\because DG // AB$,$\therefore \angle EBD = \angle BDG$,$\therefore \angle EDB = \angle BDG$。
在$\triangle BEG$和$\triangle DGE$中,$\begin{cases} \angle BEG = \angle DGE, \\ EG = EG, \\ \angle BGE = \angle DEG, \end{cases}$ $\therefore \triangle BEG \cong \triangle DGE(ASA)$,
$\therefore DG = BE$,$\therefore DG = ED$,$\therefore BD \perp EG$(三线合一)。
(1)设$\angle ACB = x$,则$\angle ABC = 2x$,$\angle BAC = 3x$,$\because \angle ACB + \angle ABC + \angle BAC = 180^{\circ}$,$\therefore x + 2x + 3x = 180^{\circ}$,$\therefore x = 30^{\circ}$,$\therefore \angle ABC = 2x = 60^{\circ}$,$\angle BAC = 3x = 90^{\circ}$,$\because BD$平分$\angle ABC$,$\therefore \angle ABD = 30^{\circ}$,$\because AD \perp BD$,$\therefore \angle BAD = 90^{\circ} - 30^{\circ} = 60^{\circ}$,$\therefore \angle DAC = \angle BAC - \angle BAD = 90^{\circ} - 60^{\circ} = 30^{\circ}$。
(2)$\angle DAF = \angle C$。
理由:$\because EF // BC$,$\angle BED = 128^{\circ}$,$\therefore \angle ABC = 180^{\circ} - \angle BED = 180^{\circ} - 128^{\circ} = 52^{\circ}$,$\because BD$平分$\angle ABC$,$\therefore \angle ABD = \frac{1}{2} \angle ABC = \frac{1}{2} \times 52^{\circ} = 26^{\circ}$。
$\because AD \perp BD$,$\therefore \angle BAD = 90^{\circ} - 26^{\circ} = 64^{\circ}$,$\because \angle DAF = \frac{1}{2} \angle BAD = \frac{1}{2} \times 64^{\circ} = 32^{\circ}$,$\therefore \angle BAC = \angle BAD + \angle DAF = 64^{\circ} + 32^{\circ} = 96^{\circ}$,$\therefore \angle C = 180^{\circ} - \angle BAC - \angle ABC = 180^{\circ} - 96^{\circ} - 52^{\circ} = 32^{\circ}$,$\therefore \angle DAF = \angle C$。
(3)$BD \perp EG$。理由:$\because EF // BC$,$\therefore \angle EDB = \angle DBC$,$\because BD$平分$\angle ABC$,$\therefore \angle EBD = \angle DBG$,$\therefore \angle EBD = \angle EDB$,$\therefore BE = ED$。
$\because DG // AB$,$\therefore \angle EBD = \angle BDG$,$\therefore \angle EDB = \angle BDG$。
在$\triangle BEG$和$\triangle DGE$中,$\begin{cases} \angle BEG = \angle DGE, \\ EG = EG, \\ \angle BGE = \angle DEG, \end{cases}$ $\therefore \triangle BEG \cong \triangle DGE(ASA)$,
$\therefore DG = BE$,$\therefore DG = ED$,$\therefore BD \perp EG$(三线合一)。
查看更多完整答案,请扫码查看


