第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
9. 如图,在$\triangle ABC$中,$AB = AC = 6$,点D在边AC上,AD的垂直平分线交BC于点E.若$\angle AED = \angle B$,$CE = 3BE$,则CD等于 (

A. $\frac{3}{2}$
B. 2
C. $\frac{8}{3}$
D. 3
B
)
A. $\frac{3}{2}$
B. 2
C. $\frac{8}{3}$
D. 3
答案:
B 解析:$ \because AB = AC = 6 $,$ \therefore \angle B = \angle C $。$ \because \angle AED = \angle B $,$ \angle BAE = 180^{\circ} - \angle B - \angle AEB $,$ \angle CED = 180^{\circ} - \angle AED - \angle AEB $,$ \therefore \angle BAE = \angle CED $。$ \because AD $ 的垂直平分线交 BC 于点 E,$ \therefore AE = DE $,由 AAS 得 $ \triangle ABE \cong \triangle ECD $,$ \therefore CE = AB = 6 $,$ BE = CD $。$ \because CE = 3BE $,$ \therefore CD = BE = 2 $。
10. (2024·北京校级月考)如图,四边形ABCD中,$AB = AD$,点B关于AC的对称点$B'$恰好落在CD上,若$\angle BAD = \alpha$,则$\angle ACB =$ ( )

A. $45^{\circ}$
B. $\alpha - 45^{\circ}$
C. $\frac{1}{2}\alpha$
D. $90^{\circ} - \frac{1}{2}\alpha$

A. $45^{\circ}$
B. $\alpha - 45^{\circ}$
C. $\frac{1}{2}\alpha$
D. $90^{\circ} - \frac{1}{2}\alpha$
答案:
D 解析:如图,连接 $ AB' $,$ BB' $,过点 A 作 $ AE \perp CD $ 于点 E,由轴对称的性质可知,AC 垂直平分 $ BB' $,$ AB = AB' $,$ \angle BAC = \angle B'AC $。$ \because AB = AD $,$ \therefore AD = AB' $。又 $ \because AE \perp CD $,$ \therefore \angle DAE = \angle B'AE $,$ \therefore \angle CAE = \frac{1}{2}\angle BAD = \frac{1}{2}\alpha $。又 $ \because \angle AEB' = 90^{\circ} $,$ \therefore \angle ACB' = 180^{\circ} - \angle AEB' - \angle CAE = 90^{\circ} - \frac{1}{2}\alpha $,$ \therefore \angle ACB = \angle ACB' = 90^{\circ} - \frac{1}{2}\alpha $。

D 解析:如图,连接 $ AB' $,$ BB' $,过点 A 作 $ AE \perp CD $ 于点 E,由轴对称的性质可知,AC 垂直平分 $ BB' $,$ AB = AB' $,$ \angle BAC = \angle B'AC $。$ \because AB = AD $,$ \therefore AD = AB' $。又 $ \because AE \perp CD $,$ \therefore \angle DAE = \angle B'AE $,$ \therefore \angle CAE = \frac{1}{2}\angle BAD = \frac{1}{2}\alpha $。又 $ \because \angle AEB' = 90^{\circ} $,$ \therefore \angle ACB' = 180^{\circ} - \angle AEB' - \angle CAE = 90^{\circ} - \frac{1}{2}\alpha $,$ \therefore \angle ACB = \angle ACB' = 90^{\circ} - \frac{1}{2}\alpha $。

11. (2024·内江中考)如图,在$\triangle ABC$中,$\angle DCE = 40^{\circ}$,$AE = AC$,$BC = BD$,则$\angle ACB$的度数为____

$100^{\circ}$
.
答案:
$ 100^{\circ} $ 解析:$ \because \angle DCE = 40^{\circ} $,$ \therefore \angle CDE + \angle CED = 180^{\circ} - \angle DCE = 140^{\circ} $。$ \because AE = AC $,$ BC = BD $,$ \therefore \angle ACE = \angle AEC $,$ \angle BCD = \angle BDC $,$ \therefore \angle ACE + \angle BCD = \angle CDE + \angle CED = 140^{\circ} $,$ \therefore \angle ACB = \angle ACE + \angle BCE = \angle ACE + \angle BCD - \angle DCE = 140^{\circ} - 40^{\circ} = 100^{\circ} $。
12. (1)(2023·西宁中考)在$\triangle ABC$中,$AB = AC$,$\angle BAC = 100^{\circ}$,点D在BC边上,连接AD,若$\triangle ABD$为直角三角形,则$\angle ADB$的度数是____.
(2)在$\triangle ABC$中,$\angle B = 30^{\circ}$,点D在BC边上,点E在AC边上,$AD = BD$,$DE = CE$,若$\triangle ADE$为等腰三角形,则$\angle C$的度数为____.
(2)在$\triangle ABC$中,$\angle B = 30^{\circ}$,点D在BC边上,点E在AC边上,$AD = BD$,$DE = CE$,若$\triangle ADE$为等腰三角形,则$\angle C$的度数为____.
答案:
(1) $ 50^{\circ} $或 $ 90^{\circ} $ 解析:$ \because AB = AC $,$ \angle BAC = 100^{\circ} $,$ \therefore \angle B = \angle C = \frac{180^{\circ} - \angle A}{2} = 40^{\circ} $。$ \because \triangle ABD $ 为直角三角形,$ \therefore $ 可分类讨论:①当 $ \angle BAD = 90^{\circ} $ 时,如图①,$ \therefore \angle ADB = 180^{\circ} - \angle BAD - \angle B = 50^{\circ} $;②当 $ \angle ADB = 90^{\circ} $ 时,如图②。综上可知,$ \angle ADB $ 的度数是 $ 50^{\circ} $或 $ 90^{\circ} $。


(2) $ 20^{\circ} $或 $ 40^{\circ} $ 解析:如图③,$ \because AD = BD $,$ \angle B = 30^{\circ} $,$ \therefore \angle ADC = 60^{\circ} $。$ \because DE = CE $,$ \therefore $ 可设 $ \angle C = \angle EDC = \alpha $,则 $ \angle ADE = 60^{\circ} - \alpha $,$ \angle AED = 2\alpha $,根据三角形内角和定理可得,$ \angle DAE = 120^{\circ} - \alpha $。分三种情况:①当 $ AD = AE $ 时,有 $ 60^{\circ} - \alpha = 2\alpha $,解得 $ \alpha = 20^{\circ} $;②当 $ DA = DE $ 时,有 $ 120^{\circ} - \alpha = 2\alpha $,解得 $ \alpha = 40^{\circ} $;③当 $ EA = ED $ 时,有 $ 120^{\circ} - \alpha = 60^{\circ} - \alpha $,方程无解。综上所述,$ \angle C $ 的度数为 $ 20^{\circ} $或 $ 40^{\circ} $。

(1) $ 50^{\circ} $或 $ 90^{\circ} $ 解析:$ \because AB = AC $,$ \angle BAC = 100^{\circ} $,$ \therefore \angle B = \angle C = \frac{180^{\circ} - \angle A}{2} = 40^{\circ} $。$ \because \triangle ABD $ 为直角三角形,$ \therefore $ 可分类讨论:①当 $ \angle BAD = 90^{\circ} $ 时,如图①,$ \therefore \angle ADB = 180^{\circ} - \angle BAD - \angle B = 50^{\circ} $;②当 $ \angle ADB = 90^{\circ} $ 时,如图②。综上可知,$ \angle ADB $ 的度数是 $ 50^{\circ} $或 $ 90^{\circ} $。


(2) $ 20^{\circ} $或 $ 40^{\circ} $ 解析:如图③,$ \because AD = BD $,$ \angle B = 30^{\circ} $,$ \therefore \angle ADC = 60^{\circ} $。$ \because DE = CE $,$ \therefore $ 可设 $ \angle C = \angle EDC = \alpha $,则 $ \angle ADE = 60^{\circ} - \alpha $,$ \angle AED = 2\alpha $,根据三角形内角和定理可得,$ \angle DAE = 120^{\circ} - \alpha $。分三种情况:①当 $ AD = AE $ 时,有 $ 60^{\circ} - \alpha = 2\alpha $,解得 $ \alpha = 20^{\circ} $;②当 $ DA = DE $ 时,有 $ 120^{\circ} - \alpha = 2\alpha $,解得 $ \alpha = 40^{\circ} $;③当 $ EA = ED $ 时,有 $ 120^{\circ} - \alpha = 60^{\circ} - \alpha $,方程无解。综上所述,$ \angle C $ 的度数为 $ 20^{\circ} $或 $ 40^{\circ} $。

13. 如图,$\triangle ABC$中,$AC = BC$,$\angle ACB = 90^{\circ}$,点D,E分别在AB,BC上,且$AD = BE$,$BD = AC$,过E作$EF \perp AB$于F.
(1)求证:$\angle FED = \angle CED$;
(2)若$BF = \frac{5}{2}$,则CE的长为____.

(1)求证:$\angle FED = \angle CED$;
(2)若$BF = \frac{5}{2}$,则CE的长为____.

答案:
(1) 如图,连接 CD,$ \because AC = BC $,$ \angle ACB = 90^{\circ} $,$ \therefore \angle A = \angle B = 45^{\circ} $。在 $ \triangle ADC $ 和 $ \triangle BED $ 中,$ \left\{ \begin{array} { l } { A D = B E, } \\ { \angle A = \angle B, } \\ { A C = B D, } \end{array} \right. $$ \therefore \triangle ADC \cong \triangle BED (SAS) $,$ \therefore DC = DE $,$ \angle DCA = \angle EDB $,$ \therefore \angle ECD = \angle CED $,$ \angle DCA + \angle ECD = \angle EDB + \angle FED = 90^{\circ} $,$ \therefore \angle FED = \angle ECD $,$ \therefore \angle FED = \angle CED $。
(2) 5 解析:如图,过 D 作 $ DH \perp EC $ 于 H,$ \because DC = DE $,$ DH \perp EC $,$ \therefore EH = HC = \frac{1}{2}EC $,$ \angle EDH = \angle CDH $,$ \therefore DH // AC $,$ \therefore \angle CDH = \angle ACD $,$ \therefore \angle FDE = \angle EDH $。又 $ EF \perp AB $,$ EH \perp DH $,$ \therefore EF = EH = \frac{1}{2}CE $。$ \because \angle BFE = 90^{\circ} $,$ \angle B = 45^{\circ} $,$ \therefore EF = BF = \frac{5}{2} $,$ \therefore CE = 5 $。

(1) 如图,连接 CD,$ \because AC = BC $,$ \angle ACB = 90^{\circ} $,$ \therefore \angle A = \angle B = 45^{\circ} $。在 $ \triangle ADC $ 和 $ \triangle BED $ 中,$ \left\{ \begin{array} { l } { A D = B E, } \\ { \angle A = \angle B, } \\ { A C = B D, } \end{array} \right. $$ \therefore \triangle ADC \cong \triangle BED (SAS) $,$ \therefore DC = DE $,$ \angle DCA = \angle EDB $,$ \therefore \angle ECD = \angle CED $,$ \angle DCA + \angle ECD = \angle EDB + \angle FED = 90^{\circ} $,$ \therefore \angle FED = \angle ECD $,$ \therefore \angle FED = \angle CED $。
(2) 5 解析:如图,过 D 作 $ DH \perp EC $ 于 H,$ \because DC = DE $,$ DH \perp EC $,$ \therefore EH = HC = \frac{1}{2}EC $,$ \angle EDH = \angle CDH $,$ \therefore DH // AC $,$ \therefore \angle CDH = \angle ACD $,$ \therefore \angle FDE = \angle EDH $。又 $ EF \perp AB $,$ EH \perp DH $,$ \therefore EF = EH = \frac{1}{2}CE $。$ \because \angle BFE = 90^{\circ} $,$ \angle B = 45^{\circ} $,$ \therefore EF = BF = \frac{5}{2} $,$ \therefore CE = 5 $。

14. (绍兴中考)如图,钢架中焊上等长的13根钢条来加固钢架,若$AP_1 = P_1P_2 = P_2P_3 = \cdots = P_{13}P_{14} = P_{14}A$,则$\angle A$的度数是____

$12^{\circ}$
.
答案:
$ 12^{\circ} $ 解析:$ \because AP_1 = P_1P_2 = P_2P_3 = \cdots = P_{13}P_{14} = P_{14}A $,$ \therefore $ 设 $ \angle A = \angle AP_2P_1 = \angle AP_{13}P_{14} = x $,则 $ \angle P_1P_3P_2 = \angle P_2P_1P_3 = \angle P_{13}P_{14}P_{12} = \angle P_{13}P_{12}P_{14} = 2x $,$ \therefore \angle P_3P_2P_4 = \angle P_{12}P_{13}P_{11} = 3x $,$ \cdots $,$ \angle P_7P_6P_8 = \angle P_8P_9P_7 = 7x $,$ \therefore \angle AP_7P_8 = 7x $,$ \angle AP_8P_7 = 7x $。在 $ \triangle AP_7P_8 $ 中,$ \angle A + \angle AP_7P_8 + \angle AP_8P_7 = 180^{\circ} $,即 $ x + 7x + 7x = 180^{\circ} $,解得 $ x = 12^{\circ} $,即 $ \angle A = 12^{\circ} $。
15. (1)有一张三角形纸片ABC,$\angle A = 80^{\circ}$,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两纸片均为等腰三角形,则$\angle C$的度数可以是____;
(2)一个三角形可被剪成两个等腰三角形,原三角形的一个内角为$36^{\circ}$,求原三角形的最大内角的所有可能值.
(2)一个三角形可被剪成两个等腰三角形,原三角形的一个内角为$36^{\circ}$,求原三角形的最大内角的所有可能值.
答案:
(1) $ 40^{\circ} $或 $ 25^{\circ} $或 $ 10^{\circ} $ 解析:由题意知 $ \triangle ABD $ 与 $ \triangle DBC $ 均为等腰三角形,对于 $ \triangle ABD $ 可能有 ① $ AB = BD $,此时 $ \angle ADB = \angle A = 80^{\circ} $,$ \therefore \angle BDC = 180^{\circ} - \angle ADB = 100^{\circ} $,$ \angle C = \frac{1}{2} \times (180^{\circ} - 100^{\circ}) = 40^{\circ} $;② $ AB = AD $,此时 $ \angle ADB = \frac{1}{2} \times (180^{\circ} - \angle A) = 50^{\circ} $,$ \therefore \angle BDC = 180^{\circ} - \angle ADB = 130^{\circ} $,$ \angle C = \frac{1}{2} \times (180^{\circ} - 130^{\circ}) = 25^{\circ} $;③ $ AD = BD $,此时 $ \angle ADB = 180^{\circ} - 2 \times 80^{\circ} = 20^{\circ} $,$ \therefore \angle BDC = 180^{\circ} - \angle ADB = 160^{\circ} $,$ \angle C = \frac{1}{2} \times (180^{\circ} - 160^{\circ}) = 10^{\circ} $。综上所述,$ \angle C $ 的度数可以为 $ 40^{\circ} $或 $ 25^{\circ} $或 $ 10^{\circ} $。
(2) ①原三角形是锐角三角形,最大角是 $ 72^{\circ} $ 的情况:如图①,$ \angle ABC = \angle ACB = 72^{\circ} $,$ \angle A = 36^{\circ} $,$ AD = BD = BC $;
②原三角形是直角三角形,最大角是 $ 90^{\circ} $ 的情况:如图②,$ \angle ABC = 90^{\circ} $,$ \angle A = 36^{\circ} $,$ AD = BD = CD $;③原三角形是钝角三角形,最大角是 $ 108^{\circ} $ 的情况:如图③,$ \angle BAC = 108^{\circ} $,$ \angle B = 36^{\circ} $,$ BD = AB $,$ AD = DC $;④原三角形是钝角三角形,最大角是 $ 132^{\circ} $ 的情况:如图④,$ \angle C = 132^{\circ} $,$ \angle ABC = 36^{\circ} $,$ AD = BD $,$ CD = BC $;⑤原三角形是钝角三角形,最大角是 $ 126^{\circ} $ 的情况:如图⑤,$ \angle BAC = 126^{\circ} $,$ \angle C = 36^{\circ} $,$ BD = AD = AC $。
综上,原三角形的最大内角的所有可能值为 $ 72^{\circ} $,$ 90^{\circ} $,$ 108^{\circ} $,$ 132^{\circ} $或 $ 126^{\circ} $。

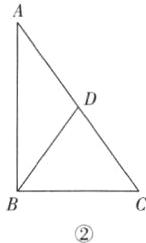
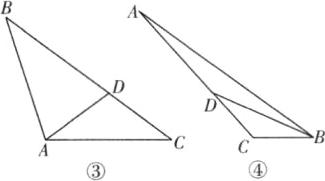

(1) $ 40^{\circ} $或 $ 25^{\circ} $或 $ 10^{\circ} $ 解析:由题意知 $ \triangle ABD $ 与 $ \triangle DBC $ 均为等腰三角形,对于 $ \triangle ABD $ 可能有 ① $ AB = BD $,此时 $ \angle ADB = \angle A = 80^{\circ} $,$ \therefore \angle BDC = 180^{\circ} - \angle ADB = 100^{\circ} $,$ \angle C = \frac{1}{2} \times (180^{\circ} - 100^{\circ}) = 40^{\circ} $;② $ AB = AD $,此时 $ \angle ADB = \frac{1}{2} \times (180^{\circ} - \angle A) = 50^{\circ} $,$ \therefore \angle BDC = 180^{\circ} - \angle ADB = 130^{\circ} $,$ \angle C = \frac{1}{2} \times (180^{\circ} - 130^{\circ}) = 25^{\circ} $;③ $ AD = BD $,此时 $ \angle ADB = 180^{\circ} - 2 \times 80^{\circ} = 20^{\circ} $,$ \therefore \angle BDC = 180^{\circ} - \angle ADB = 160^{\circ} $,$ \angle C = \frac{1}{2} \times (180^{\circ} - 160^{\circ}) = 10^{\circ} $。综上所述,$ \angle C $ 的度数可以为 $ 40^{\circ} $或 $ 25^{\circ} $或 $ 10^{\circ} $。
(2) ①原三角形是锐角三角形,最大角是 $ 72^{\circ} $ 的情况:如图①,$ \angle ABC = \angle ACB = 72^{\circ} $,$ \angle A = 36^{\circ} $,$ AD = BD = BC $;
②原三角形是直角三角形,最大角是 $ 90^{\circ} $ 的情况:如图②,$ \angle ABC = 90^{\circ} $,$ \angle A = 36^{\circ} $,$ AD = BD = CD $;③原三角形是钝角三角形,最大角是 $ 108^{\circ} $ 的情况:如图③,$ \angle BAC = 108^{\circ} $,$ \angle B = 36^{\circ} $,$ BD = AB $,$ AD = DC $;④原三角形是钝角三角形,最大角是 $ 132^{\circ} $ 的情况:如图④,$ \angle C = 132^{\circ} $,$ \angle ABC = 36^{\circ} $,$ AD = BD $,$ CD = BC $;⑤原三角形是钝角三角形,最大角是 $ 126^{\circ} $ 的情况:如图⑤,$ \angle BAC = 126^{\circ} $,$ \angle C = 36^{\circ} $,$ BD = AD = AC $。
综上,原三角形的最大内角的所有可能值为 $ 72^{\circ} $,$ 90^{\circ} $,$ 108^{\circ} $,$ 132^{\circ} $或 $ 126^{\circ} $。




查看更多完整答案,请扫码查看


