第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
1.(攀枝花中考)如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带哪一块或两块去最省事? (
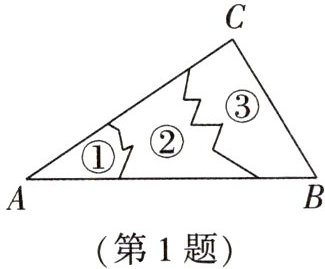
A. ①
B. ②
C. ③
D. ①③
C
)
A. ①
B. ②
C. ③
D. ①③
答案:
C
2.(2023·凉山州中考)如图,点E,F在BC上,BE=CF,∠B=∠C,添加一个条件,不能证明△ABF≌△DCE的是 (
A. ∠A=∠D B. ∠AFB=∠DEC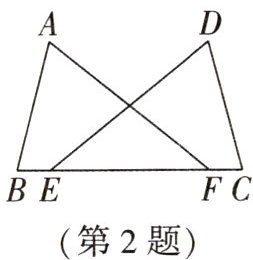
C. AB=DC D. AF=DE
D
)A. ∠A=∠D B. ∠AFB=∠DEC

C. AB=DC D. AF=DE
答案:
D
3.(2024·襄阳月考)根据下列条件能画出唯一△ABC的是 (
A. AB=3,BC=4,AC=8
B. AB=4,BC=3,∠A=30°
C. ∠A=30°,∠B=70°,∠C=80°
D. ∠A=60°,∠B=30°,AB=4
D
)A. AB=3,BC=4,AC=8
B. AB=4,BC=3,∠A=30°
C. ∠A=30°,∠B=70°,∠C=80°
D. ∠A=60°,∠B=30°,AB=4
答案:
D
4.(牡丹江中考改编)如图,已知∠ACD=∠BCE,AC=DC,当添加条件

∠A = ∠D
时,可依据"ASA"证明△ACB≌△DCE;当添加条件∠B = ∠E
时,可依据"AAS"证明△ACB≌△DCE.(不添加辅助线和字母)
答案:
$∠A = ∠D$ $∠B = ∠E$
5.(临沂中考改编)如图,AB//CF,E为DF的中点,若AB=9cm,CF=6cm,则BD=
3
cm.
答案:
3
6.(长沙中考)如图,AC平分∠BAD,CB⊥AB,CD⊥AD,垂足分别为B,D.
(1)求证:△ABC≌△ADC;
证明:∵AC平分∠BAD,∴∠BAC=∠DAC。∵CB⊥AB,CD⊥AD,∴∠B=90°=∠D。在△ABC和△ADC中,$\left\{ \begin{array} { l } { ∠B = ∠D, } \\ { ∠BAC = ∠DAC, } \\ { AC = AC, } \end{array} \right.$∴△ABC≌△ADC(AAS)。
(2)若AB=4,CD=3,求四边形ABCD的面积.
解:由(1)知,△ABC≌△ADC,∴BC=CD=3,S△ABC=S△ADC,∴S△ABC=$\frac{1}{2}$AB·BC=$\frac{1}{2}$×4×3=6,∴S△ADC=6,∴S四边形ABCD=S△ABC+S△ADC=
(1)求证:△ABC≌△ADC;
证明:∵AC平分∠BAD,∴∠BAC=∠DAC。∵CB⊥AB,CD⊥AD,∴∠B=90°=∠D。在△ABC和△ADC中,$\left\{ \begin{array} { l } { ∠B = ∠D, } \\ { ∠BAC = ∠DAC, } \\ { AC = AC, } \end{array} \right.$∴△ABC≌△ADC(AAS)。
(2)若AB=4,CD=3,求四边形ABCD的面积.
解:由(1)知,△ABC≌△ADC,∴BC=CD=3,S△ABC=S△ADC,∴S△ABC=$\frac{1}{2}$AB·BC=$\frac{1}{2}$×4×3=6,∴S△ADC=6,∴S四边形ABCD=S△ABC+S△ADC=
12
。
答案:
(1) $∵$ AC平分$∠BAD$,$∴ ∠BAC = ∠DAC$。$∵ CB ⊥ AB$,$CD ⊥ AD$,$∴ ∠B = 90° = ∠D$。在$△ABC$和$△ADC$中,$\left\{ \begin{array} { l } { ∠B = ∠D, } \\ { ∠BAC = ∠DAC, } \\ { AC = AC, } \end{array} \right.$ $∴ △ABC ≌ △ADC (AAS)$。
(2) 由
(1)知,$△ABC ≌ △ADC$,$∴ BC = CD = 3$,$S_{△ABC} = S_{△ADC}$,$∴ S_{△ABC} = \frac { 1 } { 2 } AB \cdot BC = \frac { 1 } { 2 } × 4 × 3 = 6$,$∴ S_{△ADC} = 6$,$∴ S_{四边形ABCD} = S_{△ABC} + S_{△ADC} = 12$。
(1) $∵$ AC平分$∠BAD$,$∴ ∠BAC = ∠DAC$。$∵ CB ⊥ AB$,$CD ⊥ AD$,$∴ ∠B = 90° = ∠D$。在$△ABC$和$△ADC$中,$\left\{ \begin{array} { l } { ∠B = ∠D, } \\ { ∠BAC = ∠DAC, } \\ { AC = AC, } \end{array} \right.$ $∴ △ABC ≌ △ADC (AAS)$。
(2) 由
(1)知,$△ABC ≌ △ADC$,$∴ BC = CD = 3$,$S_{△ABC} = S_{△ADC}$,$∴ S_{△ABC} = \frac { 1 } { 2 } AB \cdot BC = \frac { 1 } { 2 } × 4 × 3 = 6$,$∴ S_{△ADC} = 6$,$∴ S_{四边形ABCD} = S_{△ABC} + S_{△ADC} = 12$。
7.(2024·衡阳期末)如图,∠E=∠F=90°,∠B=∠C,BE=CF,给出下列结论:①∠1=∠2;②AE=AF;③△ACN≌△ABM;④CD=AE.其中正确的结论有 (

A. 1个
B. 2个
C. 3个
D. 4个
C
)
A. 1个
B. 2个
C. 3个
D. 4个
答案:
C 解析:根据三角形的内角和定理求出$∠EAB = ∠FAC$,进而得出$∠1 = ∠2$,$∴$①正确。根据ASA证明$△EAB ≌ △FAC$,$∴ AE = AF$,$AB = AC$,$∴$②正确。根据ASA证明$△ACN ≌ △ABM$,$∴$③正确。根据已知不能推出$CD = AE$,$∴$④错误。
8.(南京中考)如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为 (
A. a+c B. b+c C. a-b+c D. a+b-c

D
)A. a+c B. b+c C. a-b+c D. a+b-c

答案:
D 解析:$∵ AB ⊥ CD$,$CE ⊥ AD$,$BF ⊥ AD$,$∴ ∠AFB = ∠CED = 90°$,$∠A + ∠D = 90°$,$∠C + ∠D = 90°$,$∴ ∠A = ∠C$。$∵ AB = CD$,$∴ △ABF ≌ △CDE (AAS)$,$∴ AF = CE = a$,$BF = DE = b$。$∵ EF = c$,$∴ AD = AF + DF = a + (b - c) = a + b - c$。
归纳总结
常见的隐含的等角:①公共角相等;②对顶角相等;③等角加(或减)等角,其和(或差)仍相等;④同角或等角的余(或补)角相等;⑤平行线的同位角相等、内错角相等;⑥三角形内角和或外角性质得到等角。
归纳总结
常见的隐含的等角:①公共角相等;②对顶角相等;③等角加(或减)等角,其和(或差)仍相等;④同角或等角的余(或补)角相等;⑤平行线的同位角相等、内错角相等;⑥三角形内角和或外角性质得到等角。
9.(2025·新乡期末)如图,在△ABC中,AB=BC,∠ABC=90°,若点A(-3,3),B(0,-2),则点C的坐标为 ( )
A. (4,1) B. (5,2) C. (5,1) D. (6,2)
A. (4,1) B. (5,2) C. (5,1) D. (6,2)

答案:
C 解析:过点A作$AE ⊥ y$轴于点E,过点C作$CF ⊥ y$轴于点F,如图,
$∵ ∠ABC = 90°$,$∴ ∠ABE + ∠CBE = ∠CBE + ∠BCF = 90°$,$∴ ∠ABE = ∠BCF$。
$∵ AB = BC$,$∴ △ABE ≌ △BCF (AAS)$,
$∴ BF = AE$,$BE = CF$;$∵$点$A(-3, 3)$,$B(0, -2)$,$∴ AE = OE = 3$,$OB = 2$,$∴ CF = BE = 3 - (-2) = 5$,$OF = BF - OB = AE - OB = 3 - 2 = 1$,$∴ C(5, 1)$。故选C。

C 解析:过点A作$AE ⊥ y$轴于点E,过点C作$CF ⊥ y$轴于点F,如图,
$∵ ∠ABC = 90°$,$∴ ∠ABE + ∠CBE = ∠CBE + ∠BCF = 90°$,$∴ ∠ABE = ∠BCF$。
$∵ AB = BC$,$∴ △ABE ≌ △BCF (AAS)$,
$∴ BF = AE$,$BE = CF$;$∵$点$A(-3, 3)$,$B(0, -2)$,$∴ AE = OE = 3$,$OB = 2$,$∴ CF = BE = 3 - (-2) = 5$,$OF = BF - OB = AE - OB = 3 - 2 = 1$,$∴ C(5, 1)$。故选C。

查看更多完整答案,请扫码查看


