第115页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
1. 教材 P119 活动 1 变式 (2025·孝感期末)
月历中有很多奥秘,我们可以发现其中某些数满足一定的规律.如图是 2024 年 12 月份的月历,用一个长方形任意框出 4 个数,将这 4 个数先平方,然后交叉相加,再相减,结果都是一定的,例如:
$(2^{2}+10^{2})-(3^{2}+9^{2})=14,$
$(12^{2}+20^{2})-(13^{2}+19^{2})=14.$
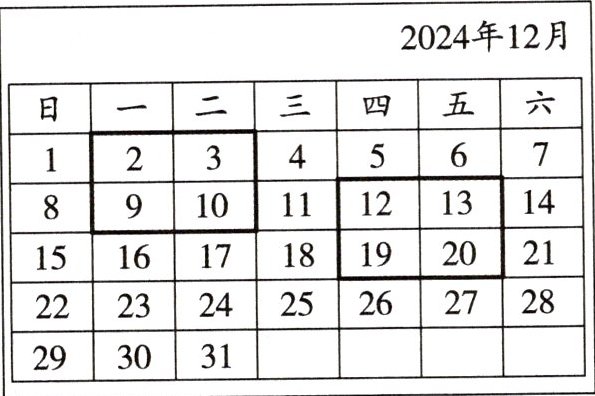
(1)请你用这个长方形再框出 4 个数,验算一下,看看是否符合这个规律;
答案不唯一,示例:框出的数如图.
![img alt=1-1]
验证为$(4^{2}+12^{2})-(5^{2}+11^{2})=14$.
(2)把框出的 4 个数中左上角的数记为 $ n $,请用含 $ n $ 的式子把这个规律表示出来;
(3)请利用整式的运算对以上规律加以证明.
$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]$
$=n^{2}+n^{2}+16n+64-n^{2}-2n-1-n^{2}-14n-49$
$=14$,则$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]=14$成立.
月历中有很多奥秘,我们可以发现其中某些数满足一定的规律.如图是 2024 年 12 月份的月历,用一个长方形任意框出 4 个数,将这 4 个数先平方,然后交叉相加,再相减,结果都是一定的,例如:
$(2^{2}+10^{2})-(3^{2}+9^{2})=14,$
$(12^{2}+20^{2})-(13^{2}+19^{2})=14.$

(1)请你用这个长方形再框出 4 个数,验算一下,看看是否符合这个规律;
答案不唯一,示例:框出的数如图.
![img alt=1-1]
验证为$(4^{2}+12^{2})-(5^{2}+11^{2})=14$.
(2)把框出的 4 个数中左上角的数记为 $ n $,请用含 $ n $ 的式子把这个规律表示出来;
左上角的数记为$n$,则右上角的数为$n + 1$,左下角的数为$n + 7$,右下角的数为$n + 8$,由题意可得$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]=14$.
(3)请利用整式的运算对以上规律加以证明.
$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]$
$=n^{2}+n^{2}+16n+64-n^{2}-2n-1-n^{2}-14n-49$
$=14$,则$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]=14$成立.
答案:
(1)答案不唯一,示例:框出的数如图.
![img alt=1-1]
验证为$(4^{2}+12^{2})-(5^{2}+11^{2})=14$.
(2)左上角的数记为$n$,则右上角的数为$n + 1$,左下角的数为$n + 7$,右下角的数为$n + 8$,由题意可得$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]=14$.
(3)$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]$
$=n^{2}+n^{2}+16n+64-n^{2}-2n-1-n^{2}-14n-49$
$=14$,则$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]=14$成立.
(1)答案不唯一,示例:框出的数如图.
![img alt=1-1]
验证为$(4^{2}+12^{2})-(5^{2}+11^{2})=14$.
(2)左上角的数记为$n$,则右上角的数为$n + 1$,左下角的数为$n + 7$,右下角的数为$n + 8$,由题意可得$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]=14$.
(3)$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]$
$=n^{2}+n^{2}+16n+64-n^{2}-2n-1-n^{2}-14n-49$
$=14$,则$[n^{2}+(n+8)^{2}]-[(n+1)^{2}+(n+7)^{2}]=14$成立.
2. (2025·遵义期末)
从边长为 $ a $ 的正方形中剪掉一个边长为 $ b $ 的正方形(如图①),然后将剩余部分拼成一个长方形(如图②).
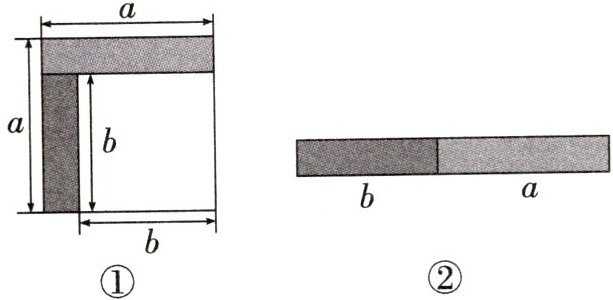
(1)根据图②长方形的面积与图①中阴影部分的面积相等可以验证的等式是
(2)小明根据以上操作去计算 $ (a + 1)(a^{2}+1) $时发现只需要在前面乘一个 $ \frac{a - 1}{a - 1} $即可得到:
$\left(\frac{a - 1}{a - 1}\right)(a + 1)(a^{2}+1)=\left(\frac{a^{2}-1}{a - 1}\right)(a^{2}+1)=\frac{a^{4}-1}{a - 1},$
请根据以上规律计算: $ (a + 1)(a^{2}+1)\cdot(a^{4}+1)\cdots(a^{32}+1)= $
(3)运用以上规律计算 $ (5 + 1)×(5^{2}+1)×(5^{4}+1)×\cdots×(5^{64}+1) $.
解:原式=
从边长为 $ a $ 的正方形中剪掉一个边长为 $ b $ 的正方形(如图①),然后将剩余部分拼成一个长方形(如图②).

(1)根据图②长方形的面积与图①中阴影部分的面积相等可以验证的等式是
$a^{2}-b^{2}=(a+b)(a-b)$
.(2)小明根据以上操作去计算 $ (a + 1)(a^{2}+1) $时发现只需要在前面乘一个 $ \frac{a - 1}{a - 1} $即可得到:
$\left(\frac{a - 1}{a - 1}\right)(a + 1)(a^{2}+1)=\left(\frac{a^{2}-1}{a - 1}\right)(a^{2}+1)=\frac{a^{4}-1}{a - 1},$
请根据以上规律计算: $ (a + 1)(a^{2}+1)\cdot(a^{4}+1)\cdots(a^{32}+1)= $
$\frac{a^{64}-1}{a - 1}$
.(3)运用以上规律计算 $ (5 + 1)×(5^{2}+1)×(5^{4}+1)×\cdots×(5^{64}+1) $.
解:原式=
$\frac{1}{4}×(5 - 1)(5 + 1)(5^{2}+1)(5^{4}+1)×\cdots×(5^{64}+1)=\frac{1}{4}×(5^{2}-1)(5^{2}+1)(5^{4}+1)×\cdots×(5^{64}+1)=\frac{1}{4}×(5^{4}-1)(5^{4}+1)×\cdots×(5^{64}+1)=\frac{1}{4}×(5^{8}-1)\cdots×(5^{64}+1)=\frac{1}{4}×(5^{64}-1)(5^{64}+1)=\frac{5^{128}-1}{4}$
.
答案:
(1)$a^{2}-b^{2}=(a+b)(a-b)$
(2)$\frac{a^{64}-1}{a - 1}$ 解析:原式$=\frac{1}{a - 1}(a - 1)(a + 1)(a^{2}+1)(a^{4}+1)\cdots(a^{32}+1)=\frac{1}{a - 1}(a^{2}-1)(a^{2}+1)(a^{4}+1)\cdots(a^{32}+1)=\frac{1}{a - 1}(a^{4}-1)(a^{4}+1)\cdots(a^{32}+1)=\frac{1}{a - 1}(a^{8}-1)\cdots(a^{32}+1)=\frac{1}{a - 1}(a^{32}-1)(a^{32}+1)=\frac{a^{64}-1}{a - 1}$.
(3)原式$=\frac{1}{4}\times(5 - 1)(5 + 1)(5^{2}+1)(5^{4}+1)\times\cdots\times(5^{64}+1)=\frac{1}{4}\times(5^{2}-1)(5^{2}+1)(5^{4}+1)\times\cdots\times(5^{64}+1)=\frac{1}{4}\times(5^{4}-1)(5^{4}+1)\times\cdots\times(5^{64}+1)=\frac{1}{4}\times(5^{8}-1)\cdots\times(5^{64}+1)=\frac{1}{4}\times(5^{64}-1)(5^{64}+1)=\frac{5^{128}-1}{4}$.
(1)$a^{2}-b^{2}=(a+b)(a-b)$
(2)$\frac{a^{64}-1}{a - 1}$ 解析:原式$=\frac{1}{a - 1}(a - 1)(a + 1)(a^{2}+1)(a^{4}+1)\cdots(a^{32}+1)=\frac{1}{a - 1}(a^{2}-1)(a^{2}+1)(a^{4}+1)\cdots(a^{32}+1)=\frac{1}{a - 1}(a^{4}-1)(a^{4}+1)\cdots(a^{32}+1)=\frac{1}{a - 1}(a^{8}-1)\cdots(a^{32}+1)=\frac{1}{a - 1}(a^{32}-1)(a^{32}+1)=\frac{a^{64}-1}{a - 1}$.
(3)原式$=\frac{1}{4}\times(5 - 1)(5 + 1)(5^{2}+1)(5^{4}+1)\times\cdots\times(5^{64}+1)=\frac{1}{4}\times(5^{2}-1)(5^{2}+1)(5^{4}+1)\times\cdots\times(5^{64}+1)=\frac{1}{4}\times(5^{4}-1)(5^{4}+1)\times\cdots\times(5^{64}+1)=\frac{1}{4}\times(5^{8}-1)\cdots\times(5^{64}+1)=\frac{1}{4}\times(5^{64}-1)(5^{64}+1)=\frac{5^{128}-1}{4}$.
查看更多完整答案,请扫码查看


