《2025年学霸题中题八年级数学上册人教版》

9. 如图，长为 $ 10 $，宽为 $ 6 $ 的长方形，在 $ 4 $ 个角处各剪去 $ 1 $ 个边长为 $ x $ 的小正方形，按折痕做成一个有底无盖的长方体盒子，则该盒子的体积为$4x^{3}-32x^{2}+60x$。(用含 $ x $ 的式子表示)

答案： $4x^{3}-32x^{2}+60x$ 解析:$V=x(10-2x)(6-2x)=x(4x^{2}-32x+60)=4x^{3}-32x^{2}+60x$.

10. 如图是一个长方形娱乐场，其宽为 $ a $、长为 $ \frac { 3 } { 2 } a $，在这个娱乐场中有一个长为 $ \frac { 2 } { 5 } a $、宽为 $ \frac { 1 } { 3 } a $ 的长方形游泳池和一个直径为 $ \frac { 1 } { 2 } a $ 的半圆形活动场，剩下的部分为草坪，则草坪的面积是$(\frac {41}{30}-\frac {π}{32})a^{2}$。(用含 $ a $ 的式子表示)

答案： $(\frac {41}{30}-\frac {π}{32})a^{2}$ 解析: 草坪的面积为$\frac {3}{2}a\cdot a-\frac {2}{5}a\cdot \frac {1}{3}a-\frac {1}{2}π\cdot (\frac {1}{2}×\frac {a}{2})^{2}=\frac {3}{2}a^{2}-\frac {2}{15}a^{2}-\frac {π}{32}a^{2}=(\frac {41}{30}-\frac {π}{32})a^{2}$.

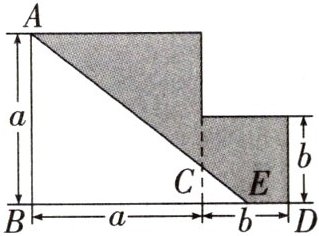
11. (2025·厦门期末)为筹备 2025 年春节花展，厦门市园博苑计划培育两种新引进的花卉。如图所示，目前有一块由两个边长分别为 $ a $ 米，$ b $ 米的正方形组成的不规则闲置地块可用于花卉培育。工作人员取小正方形边 $ C D $ 的中点 $ E $，沿 $ A E $ 将该地块分割成两个小地块，分别用于培育两种花卉。
(1)请用含有 $ a $，$ b $ 的代数式表示两个地块的面积；
两个地块的面积分别为$\frac {1}{2}a^{2}+\frac {1}{4}ab$和$\frac {1}{2}a^{2}+b^{2}-\frac {1}{4}ab$。
(2)若 $ a = 2 b $，判断工作人员的做法能否使两种花卉的培育面积相等，并说明理由。
工作人员的做法能使两种花卉的培育面积相等，理由如下：当$a=2b$时，两个地块的面积都为$\frac {5}{2}b^{2}$，所以面积相等。

答案：
(1)$\because$ 点$E$是$CD$的中点,$\therefore BE=BC+CE=BC+\frac {1}{2}CD=a+\frac {1}{2}b$,$\therefore$ 空白部分的面积$S_{△ABE}=\frac {1}{2}AB\cdot BE=\frac {1}{2}a\cdot (a+\frac {1}{2}b)=\frac {1}{2}a^{2}+\frac {1}{4}ab$,$\therefore$ 阴影部分的面积$S_{阴影}=(a^{2}+b^{2})-S_{△ABE}=a^{2}+b^{2}-\frac {1}{2}a^{2}-\frac {1}{4}ab=\frac {1}{2}a^{2}+b^{2}-\frac {1}{4}ab$.
(2) 工作人员的做法能使两种花卉的培育面积相等, 理由如下:
当$a=2b$时,$S_{△ABE}=\frac {1}{2}a^{2}+\frac {1}{4}ab=\frac {1}{2}×(2b)^{2}+\frac {1}{4}×2b\cdot b=2b^{2}+\frac {1}{2}b^{2}=\frac {5}{2}b^{2}$,$S_{阴影}=\frac {1}{2}a^{2}+b^{2}-\frac {1}{4}ab=\frac {1}{2}×(2b)^{2}+b^{2}-\frac {1}{4}×2b\cdot b=\frac {5}{2}b^{2}$,$\therefore S_{△ABE}=S_{阴影}$,$\therefore$ 工作人员的做法能使两种花卉的培育面积相等.

12. (2025·南京月考)观察下列算式：① $ ( a - 1 ) ( a + 1 ) = a ^ { 2 } - 1 $；② $ ( a - 1 ) ( a ^ { 2 } + a + 1 ) = a ^ { 3 } - 1 $；③ $ ( a - 1 ) ( a ^ { 3 } + a ^ { 2 } + a + 1 ) = a ^ { 4 } - 1 $；…；结合你观察到的规律判断 $ 2 ^ { 2025 } + 2 ^ { 2024 } + \cdots + 2 ^ { 2 } + 2 + 1 $ 的计算结果的末位数字为____3____。

答案： 3 解析:$\because$ ①$(a-1)(a+1)=a^{2}-1$; ②$(a-1)(a^{2}+a+1)=a^{3}-1$; ③$(a-1)(a^{3}+a^{2}+a+1)=a^{4}-1$;$\cdots$,$\therefore (a-1)(a^{n-1}+a^{n-2}+\cdots +1)=a^{n}-1$,$\therefore 2^{2025}+2^{2024}+\cdots +2^{2}+2+1=(2-1)(2^{2025}+2^{2024}+\cdots +2^{2}+2+1)=2^{2026}-1$.$\because 2^{1}=2$,$2^{2}=4$,$2^{3}=8$,$2^{4}=16$,$2^{5}=32$,$2^{6}=64$,$2^{7}=128$,$2^{8}=256$,$\cdots$,$\therefore 2$的乘方运算, 其末位数字分别为$2,4,8,6$, 每$4$个为一组, 依次循环.$\because 2026÷4=506\cdots \cdots 2$,$\therefore 2^{2026}$的末位数字为$4$,$\therefore 2^{2026}-1$的末位数字为$3$, 即$2^{2025}+2^{2024}+\cdots +2^{2}+2+1$的计算结果的末位数字为$3$.

13. (2025·青岛期末)归纳是发现数学结论、解决数学问题的一种重要策略，请用归纳策略解答下列问题。
(1)如图①，将一根绳子折 1 次，然后按如图所示方式剪开，剪 1 刀，绳子变为 3 段；如图②，剪 2 刀，绳子变为 5 段……剪 n 刀，绳子将变为2n+1段。
(2)如图③，按如图所示方式，将一根绳子折 2 次，剪 1 刀，绳子变为 4 段；如图④，将一根绳子折 3 次，剪 1 刀，绳子变为 5 段……将一根绳子折 m 次，剪 1 刀，绳子将变为m+2段。
(3)归纳：将一根绳子按(1)和(2)方式，折 m 次 ( m ≥ 1 )，然后剪 n 刀 ( n ≥ 1 )，绳子将变为多少段？写出你的探究过程。
(4)问题解决：若将一根绳子按(1)和(2)方式折、剪(折、剪次数 ≥ 1 )，恰好变为 95 段，会有哪几种方案？请直接写出答案。

答案：
(1)$(2n+1)$ 解析: 将一根绳子折$1$次, 剪$1$刀, 绳子变为$3$段; 剪$2$刀, 绳子变为$5$段;$\cdots \cdots$ 剪$n$刀, 绳子将变为$(2n+1)$段.
(2)$(m+2)$ 解析: 将一根绳子折$2$次, 剪$1$刀, 绳子变为$4$段; 将一根绳子折$3$次, 剪$1$刀, 绳子变为$5$段;$\cdots \cdots$ 将一根绳子折$m$次, 剪$1$刀, 绳子将变为$(m+2)$段.
(3) 由
(2) 知, 将一根绳子折$m$次, 剪$1$刀, 绳子变为$(m+2)$段, 然后剪$2$刀, 绳子段数变为$(m+2)+(m+1)(2-1)$; 剪$3$刀, 绳子段数变为$(m+2)+(m+1)(3-1)$;$\cdots \cdots$ 剪$n$刀, 绳子段数将变为$(m+2)+(m+1)(n-1)=(m+1)+1+n(m+1)-(m+1)=1+n(m+1)=mn+n+1$.
(4) 会有折$93$次、剪$1$刀, 折$1$次, 剪$47$刀, 折$46$次、剪$2$刀, 共$3$种方案. 解析: 设将一根绳子折$m$次$(m≥1)$, 然后剪$n$刀$(n≥1)$, 由
(3) 知, 绳子段数将变为$1+n(m+1)$,$\therefore$ 当$1+n(m+1)=95$时,$n(m+1)=94$,$\because 94=1×94=2×47$,$\therefore$ 当$\left\{\begin{array}{l} m+1=1,\\ n=94\end{array}\right. $或$\left\{\begin{array}{l} m+1=94,\\ n=1\end{array}\right. $时,$\left\{\begin{array}{l} m=0,\\ n=94\end{array}\right. $(舍) 或$\left\{\begin{array}{l} m=93,\\ n=1\end{array}\right. $; 当$\left\{\begin{array}{l} m+1=2,\\ n=47\end{array}\right. $或$\left\{\begin{array}{l} m+1=47,\\ n=2\end{array}\right. $时,$\left\{\begin{array}{l} m=1,\\ n=47\end{array}\right. $或$\left\{\begin{array}{l} m=46,\\ n=2\end{array}\right. $, 故会有折$93$次、剪$1$刀, 折$1$次、剪$47$刀, 折$46$次、剪$2$刀, 共$3$种方案.