第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
7. (2024·恩施期中)如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于点E,BF交AC于点F,过点O作OD⊥BC于点D,下列三个结论:①∠AOB=90°+$\frac{1}{2}$∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是(

A. ①②
B. ②③
C. ①②③
D. ①③
C
)
A. ①②
B. ②③
C. ①②③
D. ①③
答案:
7.C 解析:
∵∠BAC和∠ABC的平分线AE,BF相交于点O,
∴∠OBA=$\frac{1}{2}$∠CBA,∠OAB=$\frac{1}{2}$∠CAB,
∴∠AOB=180°−∠OBA−∠OAB=180°−$\frac{1}{2}$∠CBA−$\frac{1}{2}$∠CAB=180°−$\frac{1}{2}$(180°−∠C)=90°+$\frac{1}{2}$∠C,故①正确;
∵∠C=60°,
∴∠BAC+∠ABC=120°.
∵AE,BF分别是∠BAC和∠ABC的平分线,
∴∠OAB+∠OBA=$\frac{1}{2}$(∠BAC+∠ABC)=60°,
∴∠AOB=120°,
∴∠AOF=60°,
∴∠BOE=60°,在AB上取一点H,使BH=BE.
∵BF是∠ABC的平分线,
∴∠HBO=∠EBO.在△HBO和△EBO中,$\begin{cases}BH = BE, \\ ∠HBO = ∠EBO, \\ BO = BO,\end{cases}$
∴△HBO≌△EBO(SAS),
∴∠BOH = ∠BOE = 60°,
∴∠AOH = 180° - ∠BOH = 120°,
∴∠AOH = ∠AOF = 60°。在△HAO和△FAO中,$\begin{cases}∠HAO = ∠FAO, \\ AO = AO, \\ ∠AOH = ∠AOF,\end{cases}$
∴△HAO≌△FAO(ASA),
∴AF = AH,
∴AB = BH + AH = BE + AF,故②正确;过点O作ON⊥AC于点N,OM⊥AB于点M,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴ON = OM = OD = a。
∵AB + BC + CA = 2b,
∴$S_{\triangle ABC} = \frac{1}{2}AB \cdot OM + \frac{1}{2}AC \cdot ON + \frac{1}{2}BC \cdot OD = \frac{1}{2}(AB + AC + BC) \cdot a = ab$,故③正确。综上,①②③正确,故选C.
∵∠BAC和∠ABC的平分线AE,BF相交于点O,
∴∠OBA=$\frac{1}{2}$∠CBA,∠OAB=$\frac{1}{2}$∠CAB,
∴∠AOB=180°−∠OBA−∠OAB=180°−$\frac{1}{2}$∠CBA−$\frac{1}{2}$∠CAB=180°−$\frac{1}{2}$(180°−∠C)=90°+$\frac{1}{2}$∠C,故①正确;
∵∠C=60°,
∴∠BAC+∠ABC=120°.
∵AE,BF分别是∠BAC和∠ABC的平分线,
∴∠OAB+∠OBA=$\frac{1}{2}$(∠BAC+∠ABC)=60°,
∴∠AOB=120°,
∴∠AOF=60°,
∴∠BOE=60°,在AB上取一点H,使BH=BE.
∵BF是∠ABC的平分线,
∴∠HBO=∠EBO.在△HBO和△EBO中,$\begin{cases}BH = BE, \\ ∠HBO = ∠EBO, \\ BO = BO,\end{cases}$
∴△HBO≌△EBO(SAS),
∴∠BOH = ∠BOE = 60°,
∴∠AOH = 180° - ∠BOH = 120°,
∴∠AOH = ∠AOF = 60°。在△HAO和△FAO中,$\begin{cases}∠HAO = ∠FAO, \\ AO = AO, \\ ∠AOH = ∠AOF,\end{cases}$
∴△HAO≌△FAO(ASA),
∴AF = AH,
∴AB = BH + AH = BE + AF,故②正确;过点O作ON⊥AC于点N,OM⊥AB于点M,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴ON = OM = OD = a。
∵AB + BC + CA = 2b,
∴$S_{\triangle ABC} = \frac{1}{2}AB \cdot OM + \frac{1}{2}AC \cdot ON + \frac{1}{2}BC \cdot OD = \frac{1}{2}(AB + AC + BC) \cdot a = ab$,故③正确。综上,①②③正确,故选C.
8. (2024·德阳期末)如图,在∠AOB的边OA,OB上取点M,N,连接MN,MP平分∠AMN,NP平分∠MNB,若MN=2,△PMN的面积是2,△OMN的面积是8,则△OMN的周长是______.


答案:
8.12 解析:如图,过点P作PH⊥MN于点H,PK⊥OB于点K,PL⊥AO于点L,连接PO,
∵MP平分∠AMN,NP平分∠MNB,
∴PL = PH,PK = PH,
∴PL = PK。
∵MN = 2,△PMN的面积 = $\frac{1}{2}MN \cdot PH = 2$,
∴PH = 2,
∴PK = PL = 2。
∵△POM的面积 = $\frac{1}{2}OM \cdot PL$,△PON的面积 = $\frac{1}{2}ON \cdot PK$,
∴△OMN的面积 + △PMN的面积 = △POM的面积 + △PON的面积 = $\frac{1}{2}OM \cdot PL + \frac{1}{2}ON \cdot PK = \frac{1}{2}(OM + ON) \cdot PK = 8 + 2$,
∴$\frac{1}{2}(OM + ON) \times 2 = 10$,
∴OM + ON = 10,
∴△OMN的周长 = OM + ON + MN = 10 + 2 = 12。

8.12 解析:如图,过点P作PH⊥MN于点H,PK⊥OB于点K,PL⊥AO于点L,连接PO,
∵MP平分∠AMN,NP平分∠MNB,
∴PL = PH,PK = PH,
∴PL = PK。
∵MN = 2,△PMN的面积 = $\frac{1}{2}MN \cdot PH = 2$,
∴PH = 2,
∴PK = PL = 2。
∵△POM的面积 = $\frac{1}{2}OM \cdot PL$,△PON的面积 = $\frac{1}{2}ON \cdot PK$,
∴△OMN的面积 + △PMN的面积 = △POM的面积 + △PON的面积 = $\frac{1}{2}OM \cdot PL + \frac{1}{2}ON \cdot PK = \frac{1}{2}(OM + ON) \cdot PK = 8 + 2$,
∴$\frac{1}{2}(OM + ON) \times 2 = 10$,
∴OM + ON = 10,
∴△OMN的周长 = OM + ON + MN = 10 + 2 = 12。

9. (2024·广州期中)在平面直角坐标系xOy中,对于任意点T(m,n),将点T的“元变化”定义为:当|m|>|n|时,作点T关于x轴对称的点;当|m|≤|n|时,作点T关于y轴对称的点.根据定义,解决问题:
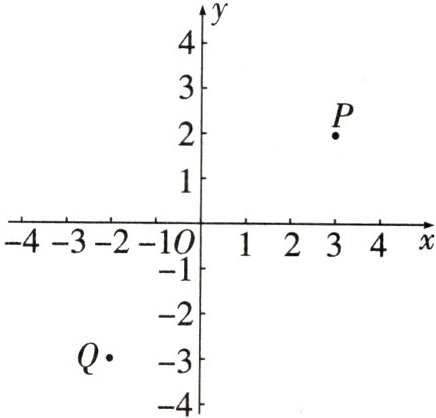
如图,点P(3,2),点Q(-2,b),其中b<-2,点P,Q“元变化”后的对应点是点P',Q'.
(1)直接写出坐标:P'______,Q'______(Q'用含b的式子表示);
(2)若PQ'=P'Q,则b的值为______.
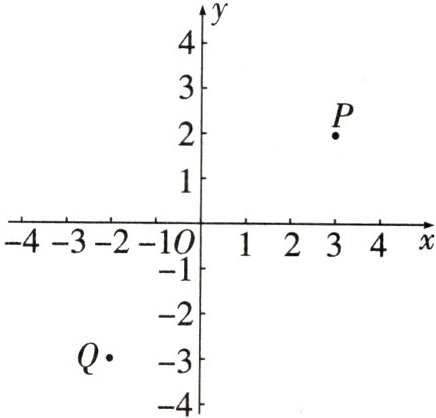
如图,点P(3,2),点Q(-2,b),其中b<-2,点P,Q“元变化”后的对应点是点P',Q'.
(1)直接写出坐标:P'______,Q'______(Q'用含b的式子表示);
(2)若PQ'=P'Q,则b的值为______.
答案:
9.
(1)(3, -2) (2, b) 解析:对于点P(3, 2),可知|3| > |2|,
∴点P'的坐标为(3, -2)。对于点Q(-2, b),其中b < -2,则|-2| < |b|,
∴点Q'的坐标为(2, b)。
(2) -3 解析:点P(3, 2),点Q(-2, b),Q'(2, b),P'(3, -2),连接P'Q',延长PP',QQ'交于点H,如图,
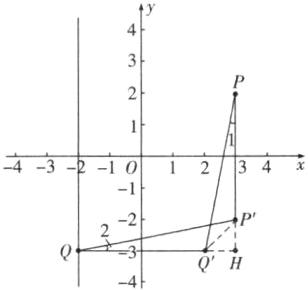
∴H(3, b),PP' = 4,QQ' = 4,
∴PP' = QQ'。而PQ' = P'Q,P'Q' = Q'P',
∴△PP'Q' ≌ △QQ'P'(SSS),
∴∠1 = ∠2。
∵∠H = ∠H = 90°,
∴△PHQ' ≌ △QHP'(AAS),
∴Q'H = P'H,
∴3 - 2 = -2 - b,解得b = -3。
9.
(1)(3, -2) (2, b) 解析:对于点P(3, 2),可知|3| > |2|,
∴点P'的坐标为(3, -2)。对于点Q(-2, b),其中b < -2,则|-2| < |b|,
∴点Q'的坐标为(2, b)。
(2) -3 解析:点P(3, 2),点Q(-2, b),Q'(2, b),P'(3, -2),连接P'Q',延长PP',QQ'交于点H,如图,

∴H(3, b),PP' = 4,QQ' = 4,
∴PP' = QQ'。而PQ' = P'Q,P'Q' = Q'P',
∴△PP'Q' ≌ △QQ'P'(SSS),
∴∠1 = ∠2。
∵∠H = ∠H = 90°,
∴△PHQ' ≌ △QHP'(AAS),
∴Q'H = P'H,
∴3 - 2 = -2 - b,解得b = -3。
10. (2024·济宁期中)如图,△ABC中,∠ABC的平分线BD和AC边的垂直平分线DE交于点D,DM⊥BA的延长线于点M,DN⊥BC于点N.若AB=3,BC=7,则AM的长为( )
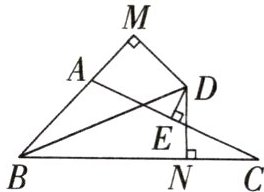
A. 1
B. 2
C. 3
D. 4

A. 1
B. 2
C. 3
D. 4
答案:
10.B 解析:连接AD,CD
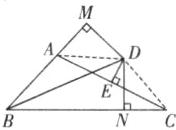
∵BD是∠ABC的平分线,
∴∠ABD = ∠DBC。
∵DM⊥BA,DN⊥BC,
∴∠DMB = ∠DNB = 90°。在△BDM和△BDN中,$\begin{cases}∠DMB = ∠DNB, \\ ∠ABD = ∠DBC, \\ BD = BD,\end{cases}$
∴△BDM ≌ △BDN(AAS),
∴BM = BN,DM = DN。
∵DE是AC的垂直平分线,
∴AD = DC。在Rt△ADM和Rt△CDN中,$\begin{cases}AD = CD, \\ DM = DN,\end{cases}$
∴Rt△ADM ≌ Rt△CDN(HL),
∴AM = CN。
∵AB = 3,BC = 7,
∴BC - AB = BN + CN - (BM - AM) = CN + AM = 2AM = 4,
∴AM = 2。
10.B 解析:连接AD,CD

∵BD是∠ABC的平分线,
∴∠ABD = ∠DBC。
∵DM⊥BA,DN⊥BC,
∴∠DMB = ∠DNB = 90°。在△BDM和△BDN中,$\begin{cases}∠DMB = ∠DNB, \\ ∠ABD = ∠DBC, \\ BD = BD,\end{cases}$
∴△BDM ≌ △BDN(AAS),
∴BM = BN,DM = DN。
∵DE是AC的垂直平分线,
∴AD = DC。在Rt△ADM和Rt△CDN中,$\begin{cases}AD = CD, \\ DM = DN,\end{cases}$
∴Rt△ADM ≌ Rt△CDN(HL),
∴AM = CN。
∵AB = 3,BC = 7,
∴BC - AB = BN + CN - (BM - AM) = CN + AM = 2AM = 4,
∴AM = 2。
查看更多完整答案,请扫码查看


