《2025年学霸题中题八年级数学上册人教版》

9. (铁岭中考)如图,在$\triangle CEF$中,$∠E=80^{\circ },∠F=50^{\circ },AB// CF,AD// CE$,连接BC,CD,则$∠A$的度数是 ( )

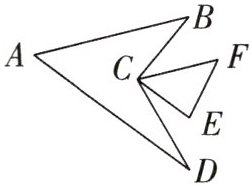
A. $45^{\circ }$
B. $50^{\circ }$
C. $55^{\circ }$
D. $80^{\circ }$

答案：
B 解析：如图，连接AC并延长，交EF于点M。
∵AB//CF，AD//CE，
∴∠3 = ∠1，∠2 = ∠4，
∴∠BAD = ∠3 + ∠4 = ∠1 + ∠2 = ∠FCE。
∵∠FCE = 180° - ∠E - ∠F = 50°，
∴∠BAD = 50°。
　　　　　　　　　　　

10. (1)(哈尔滨中考)在$\triangle ABC$中,AD为边BC上的高,$∠ABC=30^{\circ },∠CAD=20^{\circ }$,则$∠BAC$是____度.
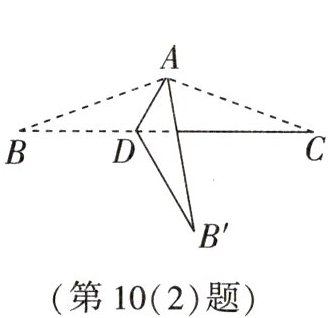
(2)(2023·辽宁中考)如图,在三角形纸片ABC中,$AB=AC,∠B=20^{\circ }$,点D是边BC上的动点,将三角形纸片沿AD对折,使点B落在点$B'$处,当$B'D⊥BC$时,$∠BAD$的度数为____.

答案：

(1) 80或40
(2) 25°或115° 解析：由折叠的性质得∠ADB' = ∠ADB。
∵B'D⊥BC，
∴∠BDB' = 90°。当B'在BC下方时，如图①。
∵∠ADB + ∠ADB' + ∠BDB' = 360°，
∴∠ADB = $\frac{1}{2}$×(360° - 90°) = 135°，
∴∠BAD = 180° - ∠B - ∠ADB = 25°；当B'在BC上方时，如图②。
∵∠ADB + ∠ADB' = 90°，
∴∠ADB = $\frac{1}{2}$×90° = 45°，
∴∠BAD = 180° - ∠B - ∠ADB = 115°。综上，∠BAD的度数为25°或115°。
　　　　　 　　

11. (抚顺中考)将两张三角形纸片如图摆放,量得$∠1+∠2+∠3+∠4=220^{\circ }$,则$∠5=$____.

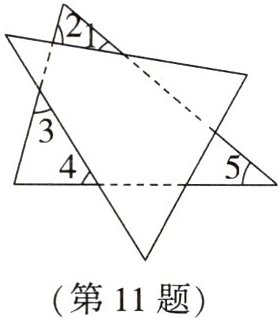
答案：
40° 解析：如图所示，∠1 + ∠2 + ∠6 = 180°，∠3 + ∠4 + ∠7 = 180°。
∵∠1 + ∠2 + ∠3 + ∠4 = 220°，∠1 + ∠2 + ∠6 + ∠3 + ∠4 + ∠7 = 360°，
∴∠6 + ∠7 = 140°，
∴∠5 = 180° - (∠6 + ∠7) = 40°。
　　　　　　　　　　

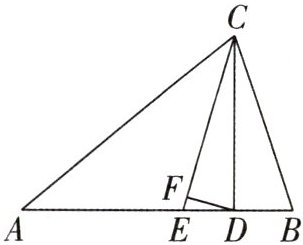
12. (1)如图,在$\triangle ABC$中,$∠A=40^{\circ },∠B=72^{\circ }$,CE平分$∠ACB$,$CD⊥AB$于D,$DF⊥CE$于F,求$∠CDF$的度数;74°
(2)在(1)中,若$∠A=α,∠B=β(α≠β)$,其他条件不变,求$∠CDF$的度数.(用含α和β的式子表示)$\frac{180° + \alpha - \beta}{2}$

答案：
(1) 在△ABC中，∠A = 40°，∠B = 72°，
∴∠ACB = 68°。又
∵CE平分∠ACB，
∴∠ACE = 34°。
∵∠A + ∠ACE + ∠AEC = 180°，∠AEC + ∠CEB = 180°，
∴∠CEB = ∠A + ∠ACE = 74°。又
∵CD⊥AB，DF⊥CE，且∠ECD为公共角，
∴∠CDF = ∠CED = 74°。
(2) 由
(1)可知，∠CDF = ∠CED = ∠A + ∠ACE，∠ACE = $\frac{180° - \alpha - \beta}{2}$，
∴∠CDF = $\frac{180° + \alpha - \beta}{2}$

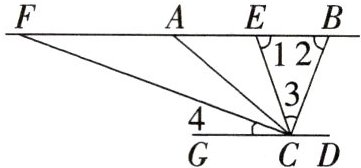
13. (2025·资阳期末)已知:三角形的三个角的和为$180^{\circ }$.如图,G,C,D三点在同一条直线上,F,A,E,B四点在同一条直线上,$CD// AB$,CB平分$∠ACD$,CF平分$∠ACG$,$∠BAC=40^{\circ },∠1=∠2$.下列结论:①$CB⊥CF$;②$∠1=70^{\circ }$;③$∠ACE=2∠4$;④$∠3=2∠4$.其中正确的是 (B)

A. ①②③
B. ①②④
C. ②③④
D. ①②③④

答案： B 解析：
∵CD//AB，∠BAC = 40°，
∴∠ACG = ∠BAC = 40°。
∵CF平分∠ACG，
∴∠4 = ∠ACF = $\frac{1}{2}$∠ACG = 20°。
∵∠ACD = 180° - ∠ACG = 140°，CB平分∠ACD，
∴∠BCD = ∠ACB = $\frac{1}{2}$∠ACD = 70°。
∴∠2 = ∠BCD = 70°。
∵∠1 = ∠2，
∴∠1 = 70°，故结论②正确；
∴∠3 = 180° - ∠1 - ∠2 = 40°，
∴∠3 = 2∠4，∠ACE = ∠ACB - ∠3 = 30°，故结论④正确；
∵∠ACE ≠ 2∠4，故结论③错误；
∵∠FCB = ∠ACF + ∠ACE + ∠3 = 20° + 30° + 40° = 90°，
∴CB⊥CF，故结论①正确。综上，正确的结论是①②④，故选B。

14. 改编题 阅读下面的材料,并解决问题.
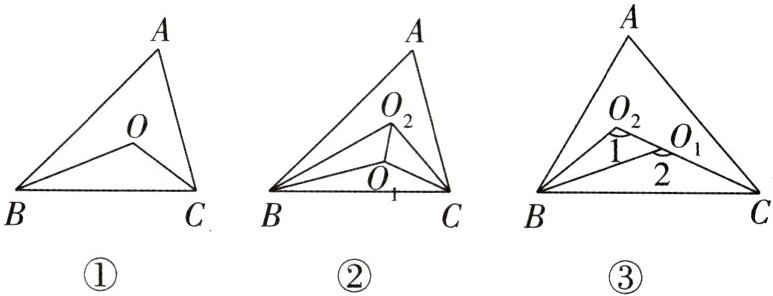
(1)如图①,在$\triangle ABC$中,$\triangle ABC$的两条内角平分线交于点O,若$∠A=60^{\circ }$,则$∠O=$120°;
(2)如图①,点O是$\triangle ABC$两条内角平分线的交点,猜想$∠O$和$∠A$的数量关系,并证明;∠O = 90° + $\frac{1}{2}$∠A。证明：∵BO平分∠ABC，CO平分∠ACB，∴∠OBC = $\frac{1}{2}$∠ABC，∠OCB = $\frac{1}{2}$∠ACB，∴∠O = 180° - (∠OBC + ∠OCB) = 180° - $\frac{1}{2}$(∠ABC + ∠ACB) = 180° - $\frac{1}{2}$(180° - ∠A) = 90° + $\frac{1}{2}$∠A。
(3)如图②,$∠ABC,∠ACB$的三等分线交于点$O_{1},O_{2}$,连接$O_{1}O_{2}$,若$∠A=60^{\circ }$,求$∠BO_{2}O_{1}$的度数;∵∠ABC，∠ACB的三等分线交于点O₁，O₂，∴∠O₂BC = $\frac{2}{3}$∠ABC，∠O₂CB = $\frac{2}{3}$∠ACB。∵BO₁平分∠O₂BC，CO₁平分∠O₂CB，∴O₂O₁平分∠BO₂C，∴∠O₂BC + ∠O₂CB = $\frac{2}{3}$(∠ABC + ∠ACB) = $\frac{2}{3}$(180° - ∠A) = 80°，∴∠BO₂C = 180° - (∠O₂BC + ∠O₂CB) = 100°，∴∠BO₂O₁ = $\frac{1}{2}$∠BO₂C = 50°。
(4)如图③,在$\triangle ABC$中,$∠ABC$的三等分线分别与$∠ACB$的平分线交于点$O_{1},O_{2}$,若$∠1=115^{\circ },∠2=135^{\circ }$,求$∠A$的度数;∵∠1 + ∠O₂BO₁ + ∠BO₁O₂ = 180°，∠BO₁O₂ + ∠2 = 180°，∴∠O₂BO₁ = ∠2 - ∠1 = 20°，∴∠ABC = 3∠O₂BO₁ = 60°，∠O₁BC = ∠O₂BO₁ = 20°，∴∠BCO₂ = 180° - 20° - 135° = 25°，∴∠ACB = 2∠BCO₂ = 50°，∴∠A = 180° - ∠ABC - ∠ACB = 70°。

答案：
(1) 120°
(2) ∠O = 90° + $\frac{1}{2}$∠A。证明：
∵BO平分∠ABC，CO平分∠ACB，
∴∠OBC = $\frac{1}{2}$∠ABC，∠OCB = $\frac{1}{2}$∠ACB，
∴∠O = 180° - (∠OBC + ∠OCB) = 180° - $\frac{1}{2}$(∠ABC + ∠ACB) = 180° - $\frac{1}{2}$(180° - ∠A) = 90° + $\frac{1}{2}$∠A。
(3)
∵∠ABC，∠ACB的三等分线交于点O₁，O₂，
∴∠O₂BC = $\frac{2}{3}$∠ABC，∠O₂CB = $\frac{2}{3}$∠ACB。
∵BO₁平分∠O₂BC，CO₁平分∠O₂CB，
∴O₂O₁平分∠BO₂C，
∴∠O₂BC + ∠O₂CB = $\frac{2}{3}$(∠ABC + ∠ACB) = $\frac{2}{3}$(180° - ∠A) = 80°，
∴∠BO₂C = 180° - (∠O₂BC + ∠O₂CB) = 100°，
∴∠BO₂O₁ = $\frac{1}{2}$∠BO₂C = 50°。
(4)
∵∠1 + ∠O₂BO₁ + ∠BO₁O₂ = 180°，∠BO₁O₂ + ∠2 = 180°，
∴∠O₂BO₁ = ∠2 - ∠1 = 20°，
∴∠ABC = 3∠O₂BO₁ = 60°，∠O₁BC = ∠O₂BO₁ = 20°，
∴∠BCO₂ = 180° - 20° - 135° = 25°，
∴∠ACB = 2∠BCO₂ = 50°，
∴∠A = 180° - ∠ABC - ∠ACB = 70°。