第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
12. (河北中考)平面内,将长分别为 1,5,1,1,d 的线段,顺次首尾相接组成凸五边形(如图),则 d 可能是 (
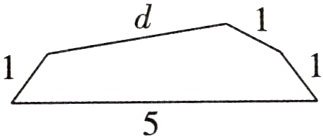
A. 1
B. 2
C. 7
D. 8
C
)
A. 1
B. 2
C. 7
D. 8
答案:
C 解析:
∵平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形,
∴1+d+1+1>5且1+5+1+1>d,
∴d的取值范围为2<d<8,则d可能是7.故选C.
∵平面内,将长分别为1,5,1,1,d的线段,顺次首尾相接组成凸五边形,
∴1+d+1+1>5且1+5+1+1>d,
∴d的取值范围为2<d<8,则d可能是7.故选C.
13. (1)已知等腰三角形三边的长分别是 4x - 2,x + 1,15 - 6x,则它的周长是____
(2) 原创题 用一根 13 m 长的绳子围成一个三角形,使得三角形的三边的长均为整数,则符合条件的三角形有____
12.3
.(2) 原创题 用一根 13 m 长的绳子围成一个三角形,使得三角形的三边的长均为整数,则符合条件的三角形有____
5
个.
答案:
(1)12.3 解析:①若4x−2=x+1,则x=1,三边长分别为2,2,9,但2+2<9,不能组成三角形,舍去;②若4x−2=15−6x,则x=1.7,三边长分别为4.8,2.7,4.8,
∴其周长为12.3;③若15−6x=x+1,则x=2,三边长分别为6,3,3,但3+3=6,不能组成三角形,舍去.
∴周长是12.3.
(2)5 解析:设三角形的三边长为a,b,c,a≤b≤c,由题意得a+b+c=13,
∴a+b=13−c>c,
∴c<$\frac{13}{2}$.又
∵a≤b≤c,
∴$\frac{13}{3}$≤c<$\frac{13}{2}$.
∵c为整数,
∴c可以为5或6,
∴三边可能的取值为3,5,5;4,4,5;1,6,6;2,5,6;3,4,6.
∴符合条件的三角形共有5个.
(1)12.3 解析:①若4x−2=x+1,则x=1,三边长分别为2,2,9,但2+2<9,不能组成三角形,舍去;②若4x−2=15−6x,则x=1.7,三边长分别为4.8,2.7,4.8,
∴其周长为12.3;③若15−6x=x+1,则x=2,三边长分别为6,3,3,但3+3=6,不能组成三角形,舍去.
∴周长是12.3.
(2)5 解析:设三角形的三边长为a,b,c,a≤b≤c,由题意得a+b+c=13,
∴a+b=13−c>c,
∴c<$\frac{13}{2}$.又
∵a≤b≤c,
∴$\frac{13}{3}$≤c<$\frac{13}{2}$.
∵c为整数,
∴c可以为5或6,
∴三边可能的取值为3,5,5;4,4,5;1,6,6;2,5,6;3,4,6.
∴符合条件的三角形共有5个.
14. 如图,在四边形 ABCD 中,AC 与 BD 交于点 O.求证:AB + BC + CD + DA > AC + BD > $\frac{1}{2}$(AB + BC + CD + DA).
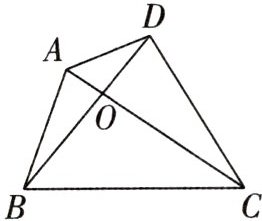

在△ABD中,AB+AD>BD,在△ABC中,AB+BC>AC,在△BCD中,BC+CD>BD,在△ACD中,AD+CD>AC,∴AB+AD+AB+BC+BC+CD+AD+CD>BD+AC+BD+AC,∴AB+BC+CD+DA>AC+BD.在△OAB中,OA+OB>AB,在△OAD中,OA+OD>AD,在△ODC中,OD+OC>CD,在△OBC中,OB+OC>BC,∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA,即2(AC+BD)>AB+BC+CD+DA,即AC+BD>$\frac{1}{2}$(AB+BC+CD+DA).∴AB+BC+CD+DA>AC+BD>$\frac{1}{2}$(AB+BC+CD+DA).
答案:
在△ABD中,AB+AD>BD,在△ABC中,AB+BC>AC,在△BCD中,BC+CD>BD,在△ACD中,AD+CD>AC,
∴AB+AD+AB+BC+BC+CD+AD+CD>BD+AC+BD+AC,
∴AB+BC+CD+DA>AC+BD.在△OAB中,OA+OB>AB,在△OAD中,OA+OD>AD,在△ODC中,OD+OC>CD,在△OBC中,OB+OC>BC,
∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA,即2(AC+BD)>AB+BC+CD+DA,即AC+BD>$\frac{1}{2}$(AB+BC+CD+DA).
∴AB+BC+CD+DA>AC+BD>$\frac{1}{2}$(AB+BC+CD+DA).
∴AB+AD+AB+BC+BC+CD+AD+CD>BD+AC+BD+AC,
∴AB+BC+CD+DA>AC+BD.在△OAB中,OA+OB>AB,在△OAD中,OA+OD>AD,在△ODC中,OD+OC>CD,在△OBC中,OB+OC>BC,
∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA,即2(AC+BD)>AB+BC+CD+DA,即AC+BD>$\frac{1}{2}$(AB+BC+CD+DA).
∴AB+BC+CD+DA>AC+BD>$\frac{1}{2}$(AB+BC+CD+DA).
15. (2024·北京期中)若三边均不相等的三角形三边 a,b,c 满足 a - b > b - c(a 为最长边,c 为最短边),则称它为“不均衡三角形”.已知某“不均衡三角形”三边分别为 2x + 2,16,2x - 6,则 x 的整数值为____
10或12或13或14
.
答案:
10或12或13或14 解析:①16−(2x+2)>2x+2−(2x−6),解得x<3.
∵2x−6>0,解得x>3,故不合题意,舍去.②2x+2>16>2x−6,解得7<x<11,2x+2−16>16−(2x−6),解得x>9,
∴9<x<11.
∵x为整数,
∴x=10,此时22,16,14可构成三角形.③2x−6>16,解得x>11,2x+2−(2x−6)>2x−6−16,解得x<15,
∴11<x<15.
∵x为整数,
∴x=12或13或14,此时都可以构成三角形.综上所述,x的整数值为10或12或13或14.
∵2x−6>0,解得x>3,故不合题意,舍去.②2x+2>16>2x−6,解得7<x<11,2x+2−16>16−(2x−6),解得x>9,
∴9<x<11.
∵x为整数,
∴x=10,此时22,16,14可构成三角形.③2x−6>16,解得x>11,2x+2−(2x−6)>2x−6−16,解得x<15,
∴11<x<15.
∵x为整数,
∴x=12或13或14,此时都可以构成三角形.综上所述,x的整数值为10或12或13或14.
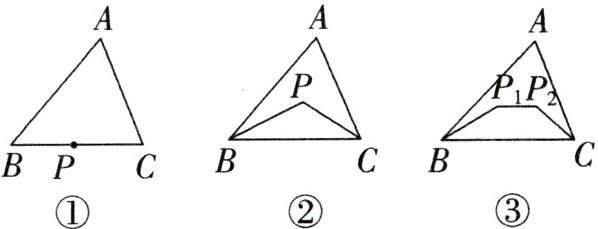
16. 观察与探究:(1)如图①,△ABC 中,P 为边 BC 上一点,比较长度大小:BP + PC____AB + AC(填“<”“=”或“>”);
(2)将(1)中点 P 移至△ABC 内,得图②,试观察比较△BPC 的周长与△ABC 的周长的大小,并说明理由;
(3)将(2)中点 P 变为两个点 P₁,P₂,得图③,试观察比较四边形 BP₁P₂C 的周长与△ABC 的周长的大小,并说明理由;
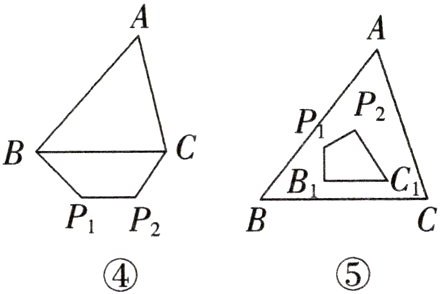
(4)将(3)中的点 P₁,P₂ 移至△ABC 外,并使点 P₁,P₂ 与点 A 在边 BC 的异侧,且∠P₁BC < ∠ABC,∠P₂CB < ∠ACB,得图④,比较周长大小:四边形 BP₁P₂C 的周长____△ABC 的周长(填“<”“=”或“>”);
(5)若将(3)中的四边形 BP₁P₂C 的顶点 B,C 移至△ABC 内,得四边形 B₁P₁P₂C₁,如图⑤,试观察比较四边形 B₁P₁P₂C₁ 的周长与△ABC 的周长的大小,并说明理由.
(2)将(1)中点 P 移至△ABC 内,得图②,试观察比较△BPC 的周长与△ABC 的周长的大小,并说明理由;
(3)将(2)中点 P 变为两个点 P₁,P₂,得图③,试观察比较四边形 BP₁P₂C 的周长与△ABC 的周长的大小,并说明理由;
(4)将(3)中的点 P₁,P₂ 移至△ABC 外,并使点 P₁,P₂ 与点 A 在边 BC 的异侧,且∠P₁BC < ∠ABC,∠P₂CB < ∠ACB,得图④,比较周长大小:四边形 BP₁P₂C 的周长____△ABC 的周长(填“<”“=”或“>”);
(5)若将(3)中的四边形 BP₁P₂C 的顶点 B,C 移至△ABC 内,得四边形 B₁P₁P₂C₁,如图⑤,试观察比较四边形 B₁P₁P₂C₁ 的周长与△ABC 的周长的大小,并说明理由.


答案:
(1)<
(2)△BPC的周长<△ABC的周长.理由如下:如图①,延长BP交AC于点M,在△ABM中,BP+PM<AB+AM,在△PMC中,PC<PM+MC,两式相加得BP+PC<AB+AC,所以△BPC的周长<△ABC的周长.
(3)四边形BP₁P₂C的周长<△ABC的周长.理由如下:如图②,分别延长BP₁,CP₂交于点M,由
(2)知,BM+CM<AB+AC,又P₁P₂<P₁M+P₂M,可得BP₁+P₁P₂+P₂C<BM+CM<AB+AC,可得结论.或作直线P₁P₂分别交AB,AC于点M,N(如图③),在△BMP₁中,BP₁<BM+MP₁,在△AMN中,MP₁+P₁P₂+P₂N<AM+AN,在△P₂NC中,P₂C<P₂N+NC,三式相加得BP₁+P₁P₂+P₂C<AB+AC,可得结论.

(4)< 解析:将四边形BP₁P₂C沿直线BC翻折,使点P₁,P₂落在△ABC内,转化为
(3)的情形,即可得结论.
(5)四边形B₁P₁P₂C₁的周长<△ABC的周长.理由如下:如图④,分别作如图所示的延长线交△ABC的边于点M,N,K,H,在△BNM中,NB₁+B₁P₁+P₁M<BM+BN,又B₁C₁+C₁K<NB₁+NC+CK,C₁P₂+P₂H<C₁K+AK+AH,P₁P₂<P₂H+MH+P₁M,将以上各式相加,得B₁P₁+P₁P₂+P₂C₁+B₁C₁<AB+BC+AC,即可得结论.
(1)<
(2)△BPC的周长<△ABC的周长.理由如下:如图①,延长BP交AC于点M,在△ABM中,BP+PM<AB+AM,在△PMC中,PC<PM+MC,两式相加得BP+PC<AB+AC,所以△BPC的周长<△ABC的周长.
(3)四边形BP₁P₂C的周长<△ABC的周长.理由如下:如图②,分别延长BP₁,CP₂交于点M,由
(2)知,BM+CM<AB+AC,又P₁P₂<P₁M+P₂M,可得BP₁+P₁P₂+P₂C<BM+CM<AB+AC,可得结论.或作直线P₁P₂分别交AB,AC于点M,N(如图③),在△BMP₁中,BP₁<BM+MP₁,在△AMN中,MP₁+P₁P₂+P₂N<AM+AN,在△P₂NC中,P₂C<P₂N+NC,三式相加得BP₁+P₁P₂+P₂C<AB+AC,可得结论.

(4)< 解析:将四边形BP₁P₂C沿直线BC翻折,使点P₁,P₂落在△ABC内,转化为
(3)的情形,即可得结论.
(5)四边形B₁P₁P₂C₁的周长<△ABC的周长.理由如下:如图④,分别作如图所示的延长线交△ABC的边于点M,N,K,H,在△BNM中,NB₁+B₁P₁+P₁M<BM+BN,又B₁C₁+C₁K<NB₁+NC+CK,C₁P₂+P₂H<C₁K+AK+AH,P₁P₂<P₂H+MH+P₁M,将以上各式相加,得B₁P₁+P₁P₂+P₂C₁+B₁C₁<AB+BC+AC,即可得结论.
查看更多完整答案,请扫码查看


