《2025年学霸题中题八年级数学上册人教版》

1. (2024·合肥期中)如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的平分线BF所在直线与射线AE相交于点G,若∠ABC=3∠C,且∠G=20°,则∠DFB的度数为(60°)
A. 50°
B. 55°
C. 60°
D. 65°

答案： 1.C　解析:
∵AE平分∠BAC,BF平分∠ABD,
∴∠CAE=∠BAE,∠ABF=∠DBF.设∠CAE=∠BAE=x,
∵∠ABC=3∠C,
∴设∠C=y,则∠ABC=3y,
∴∠ABF=∠DBF=∠CBG=$\frac{1}{2}$(180°−3y)=90°−$\frac{3}{2}$y.
∵AD⊥CD,
∴∠D=90°,
∴∠DFB=90°−∠DBF=$\frac{3}{2}$y.设∠ABF=∠DBF=∠CBG=z,则$\begin{cases}z = x + ∠G, \\ z + ∠G = x + y,\end{cases}$
∴∠G=$\frac{1}{2}$y,
∴∠DFB=3∠G.
∵∠G=20°,
∴∠DFB=60°，故选C.

2. (2024·德阳期中)设△ABC的面积为1.如图①,E₁,D₁分别是AC,BC的中点,BE₁,AD₁相交于点O₁,△BO₁D₁与△AO₁E₁的面积差记为S₁;如图②,E₂,D₂分别是AC,BC的3等分点,BE₂,AD₂相交于点O₂,△BO₂D₂与△AO₂E₂的面积差记为S₂;如图③,E₃,D₃分别是AC,BC的4等分点,BE₃,AD₃相交于点O₃,△BO₃D₃与△AO₃E₃的面积差记为S₃……依此类推,则S₂₀₂₄的值为($\frac{2023}{2025}$)
A. $\frac{2020}{2023}$
B. $\frac{2021}{2023}$
C. $\frac{2022}{2024}$
D. $\frac{2023}{2025}$

答案： 2.D　解析:由题意得$S_1 = S_{\triangle BO_1D_1} - S_{\triangle AO_1E_1} = S_{\triangle BO_1D_1} + S_{四边形 CE_1O_1D_1} - (S_{\triangle AO_1E_1} + S_{四边形 CE_1O_1D_1}) = S_{\triangle BCE_1} - S_{\triangle ACD_1}$。
∵点$E_1$，$D_1$分别是AC，BC的中点，
∴$S_{\triangle BCE_1} = \frac{1}{2}S_{\triangle ABC} = \frac{1}{2}$，$S_{\triangle ACD_1} = \frac{1}{2}S_{\triangle ABC} = \frac{1}{2}$，
∴$S_1 = S_{\triangle BCE_1} - S_{\triangle ACD_1} = 0$，同理可得$S_2 = S_{\triangle BCE_2} - S_{\triangle ACD_2} = \frac{2}{3}S_{\triangle ABC} - \frac{1}{3}S_{\triangle ABC} = \frac{1}{3}S_{\triangle ABC} = \frac{1}{3}$，$S_3 = \frac{2}{4}$，$S_4 = \frac{3}{5}$，…，
∴$S_n = \frac{n - 1}{n + 1}$，
∴$S_{2024} = \frac{2024 - 1}{2024 + 1} = \frac{2023}{2025}$。

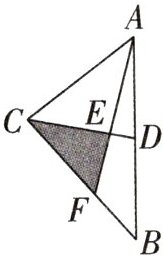
3. (2024·重庆期中)如图,在△ABC中,点D是线段AB的中点,点F将线段BC分成BF:BC=2:5,若四边形BDEF的面积是22,则△CEF的面积是______18.

答案： 3.18　解析:连接BE,设$S_{\triangle BEF} = a$，$S_{\triangle BED} = b$，
∵四边形BDEF的面积是22，
∴$S_{四边形 BDEF} = a + b = 22$。
∵点D是线段AB的中点，
∴$S_{\triangle BED} = S_{\triangle AED} = b$，$S_{\triangle BCD} = S_{\triangle ACD} = \frac{1}{2}S_{\triangle ABC}$，则$S_{\triangle ABF} = S_{\triangle AED} + S_{四边形 BDEF} = 22 + b$。
∵BF : BC = 2 : 5，则BF : CF = 2 : 3，
∴$S_{\triangle ABF} = \frac{2}{5}S_{\triangle ABC}$，$S_{\triangle BEF} = \frac{2}{3}S_{\triangle CEF}$，即$S_{\triangle ABC} = \frac{5}{2}S_{\triangle ABF} = 55 + \frac{5}{2}b$，$S_{\triangle CEF} = \frac{3}{2}S_{\triangle BEF} = \frac{3}{2}a$，则$S_{\triangle BCD} = S_{\triangle CEF} + S_{四边形 BDEF} = \frac{3}{2}a + 22 = \frac{1}{2}S_{\triangle ABC}$，
∴$\frac{3}{2}a + 22 = \frac{1}{2}(55 + \frac{5}{2}b)$，解得$a = 12$，$b = 10$，
∴$S_{\triangle CEF} = \frac{3}{2}S_{\triangle BEF} = \frac{3}{2}a = 18$。

4. (2024·哈尔滨期中)如图,AB//CD,∠BEH=$\frac{1}{n}$∠GEH,∠DFK=$\frac{1}{n}$∠GFK,∠EGF=90°,∠FPQ-∠EQP=25°,则n的值为______.

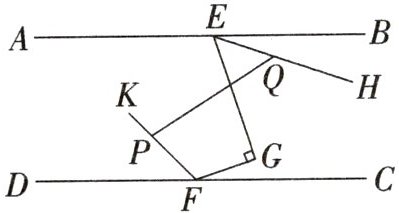
答案：
4.2.6　解析:设EG和PQ交于点O，连接OF，延长EG交CD于T，如图所示。设∠BEH = α，∠DFK = β，
∵∠BEH = $\frac{1}{n}$∠GEH，∠DFK = $\frac{1}{n}$∠GFK，
∴∠GEH = nα，∠GFK = nβ，
∴∠BEG = ∠BEH + ∠GEH = (n + 1)α，∠DFG = ∠DFK + ∠GFK = (n + 1)β，
∴∠GFT = 180° - ∠DFG = 180° - (n + 1)β。
∵AB // CD，
∴∠GTF = ∠BEG = (n + 1)α。
∵∠EGF = 90°，
∴∠FGT = 180° - ∠EGF = 90°。在△GFT中，∠GTF + ∠GFT + ∠FGT = 180°，
∴ (n + 1)α + 180° - (n + 1)β + 90° = 180°，
∴ (n + 1)(β - α) = 90° ①。
∵∠FPQ - ∠EQP = 25°，
∴∠FPQ = 25° + ∠EQP，在△OEQ中，∠GEH + ∠EQP + ∠EOQ = 180°，
∴∠EOQ = 180° - ∠GEH - ∠EQP = 180° - nα - ∠EQP，在△OPF中，∠POF + ∠PFO + ∠FPQ = 180°，在△OGF中，∠GOF + ∠GFO + ∠EGF = 180°，
∴∠POF + ∠PFO + ∠FPQ + ∠GOF + ∠GFO + ∠EGF = 360°，即∠POG + ∠GFK + ∠EGF + ∠FPQ = 360°，
∴∠POG + nβ + 90° + 25° + ∠EQP = 360°，即∠POG = 245° - nβ - ∠EQP。
∵∠EOQ = ∠POG，
∴ 180° - nα - ∠EQP = 245° - nβ - ∠EQP，
∴ n(β - α) = 65° ②，① ÷ ②得 (n + 1) : n = 90 : 65，
∴ 18n = 13(n + 1)，解得 n = 2.6。

5. (2024·湖州期中)如图,AB=AD,∠BAD=140°,AB⊥CB于点B,AD⊥CD于点D,E,F分别是CB,CD上的点,且∠EAF=70°,下列结论:①DF=BE;②△ADF≌△ABE;③FA平分∠DFE;④EF平分∠AEC;⑤BE+DF=EF.其中正确的结论是( )

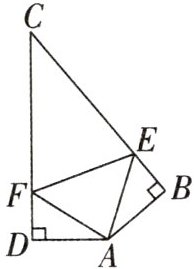
A. ④⑤
B. ①②
C. ③⑤
D. ①②③

答案：
5.C　解析:
∵E、F分别是CB，CD上的任意点，
∴DF与BE不一定相等，故①错误；
∵AB⊥CB于点B，AD⊥CD于点D，
∴∠D = ∠ABE = 90°。
∵AB = AD，
∴△ADF ≌ △ABE的另一个条件是DF = BE。
∵DF与BE不一定相等，
∴△ADF与△ABE不一定全等，故②错误；延长CB到点G，使BG = DF，连接AG，如图，则∠ABG = 180° - ∠ABE = 90°，
∴∠ABG = ∠D。在△ABG和△ADF中，$\begin{cases}AB = AD, \\ ∠ABG = ∠D, \\ BG = DF,\end{cases}$
∴△ABG ≌ △ADF(SAS)，
∴AG = AF，∠BAG = ∠DAF，
∴∠AFD = ∠AGB。
∵∠BAD = 140°，∠EAF = 70°，
∴∠EAG = ∠BAE + ∠BAG = ∠BAE + ∠DAF = ∠BAD - ∠EAF = 70°，
∴∠EAG = ∠EAF。在△EAG和△EAF中，$\begin{cases}AG = AF, \\ ∠EAG = ∠EAF, \\ AE = AE,\end{cases}$
∴△EAG ≌ △EAF(SAS)，
∴∠G = ∠AFE，∠AEB = ∠AEF，EG = EF，
∴∠AFD = ∠AFE，BE + DF = BE + BG = EG = EF，
∴FA平分∠DFE，故③⑤正确；若EF平分∠AEC，而∠AEF = ∠AEG，
∴∠CEF = ∠AEF = ∠AEG = 60°，与题干信息矛盾，故④错误。故选C.

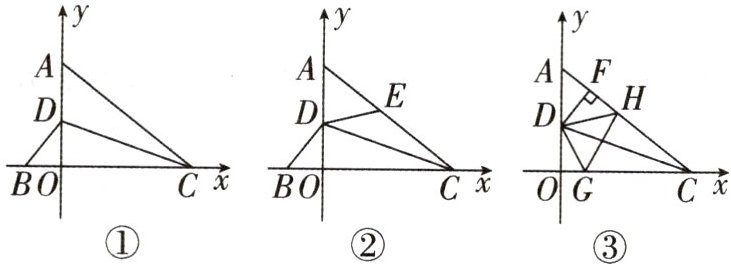
6. (2024·广州期中)如图①,点A,D在y轴正半轴上,点B,C分别在x轴上,CD平分∠ACB与y轴交于点D,∠CAO=∠DBO.
(1)求证:AC=BC;
(2)如图②,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;
(3)在(1)中,过点D作DF⊥AC于点F,点H为FC上一动点,点G为OC上一动点(如图③),当点H在FC上移动,点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH,GH,OG这三者之间的数量关系,写出你的结论并加以证明.

答案：
6.
(1)
∵CD平分∠ACB,
∴∠ACD=∠BCD.在△ACD和△BCD中，$\begin{cases}∠CAO = ∠DBO, \\ ∠ACD = ∠BCD, \\ CD = CD,\end{cases}$
∴△ACD≌△BCD(AAS),
∴AC=BC.
(2)如图①,过点D作DM⊥AC于点M,
∵CD平分∠ACB,OD⊥BC,
∴DO=DM.在△BOD和△AMD中，$\begin{cases}∠DBO = ∠DAM, \\ ∠BOD = ∠AMD = 90°, \\ DO = DM,\end{cases}$
∴△BOD≌△AMD(AAS),
∴OB=AM.在Rt△DOC和Rt△DMC中，$\begin{cases}DO = DM, \\ DC = DC,\end{cases}$
∴Rt△DOC≌Rt△DMC(HL),
∴OC=MC.
∵∠CAO = ∠DBO，∠DEA = ∠DBO，
∴∠DAE = ∠DEA。
∵DM⊥AC，
∴AM = EM，
∴OB = EM。
∵C(4, 0)，
∴OC = 4，
∴BC + CE = OB + OC + MC - EM = 2OC = 8。

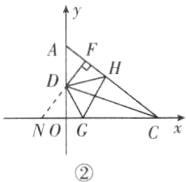
(3)GH = OG + FH.证明如下:如图②,在GO的延长线上取一点N，使ON = FH,
∵CD平分∠ACO,DF⊥AC,OD⊥OC,
∴DO=DF.在△DON和△DFH中，$\begin{cases}DO = DF, \\ ∠DON = ∠DFH = 90°, \\ ON = FH,\end{cases}$
∴△DON≌△DFH(SAS)，
∴DN=DH，∠ODN=∠FDH.
∵∠GDH=∠GDO+∠FDH,
∴∠GDH=∠GDO+∠ODN=∠GDN.在△DGN和△DGH中，$\begin{cases}DN = DH, \\ ∠GDN = ∠GDH, \\ DG = DG,\end{cases}$
∴△DGN≌△DGH(SAS)，
∴GH=GN.
∵ON=FH，
∴GH=GN=OG+ON=OG+FH.